Возьмем какое-нибудь натуральное число, например, 11. Противоположное ему будет число -11. На координатной прямой, оно находится на том же расстоянии от начала отсчета, что и число 11, только 11 находится справа, а -11 - слева. Числа 11 и -11 называются противоположными. Противоположные числа – это числа, отличающиеся только знаком. Понятно, что 0 = -0. Поэтому, число 0 противоположно самому себе.

Целые числа – это натуральные числа, противоположные им числа и 0.

Примеры целых чисел: -8, 111, 0, 1285642, -20051 и т. д.

Рациональные числа – это числа, которые можно представить в виде дроби 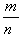, где m и n – целые числа, n ? 0. Пример: 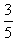; ; 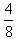; 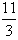1,01; 12 и т.д. Все целые числа являются рациональными.

Действительно, любое целое число n можно представить в виде дроби 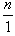. Например, целое число

18 – это .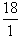

Две дроби 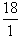считаются равными, если .

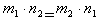Пример: 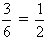= , так как 3 • 2 = 6 • 1.

Очевидно, что дроби 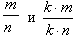равны. На этом свойстве основано сокращение дробей. Для того чтобы сократить дробь, находим общий делитель числителя и знаменателя и на этот делитель делим числитель и знаменатель - полученная дробь будет равна исходной.



Пример: Сократить дробь .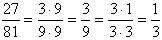



Над рациональными числами операции сложения, умножения и деления определены следующим образом:

1. Операция сложения:.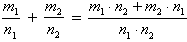



Пример: .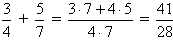



2. Операция умножения: .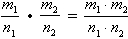



Пример: .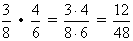



3. Операция деления: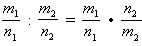, то есть, делитель «переворачиваем»



Пример: .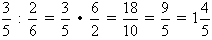



При сравнении рациональных чисел применяют следующие правила:

1. Всякое положительное рациональное число всегда больше всякого отрицательного рационального числа.



2. Если два числа 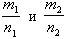положительны, то число 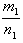больше 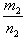, если 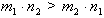, для отрицательных - наоборот.

Пример: 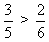, так как 3 • 6 > 5 • 2.