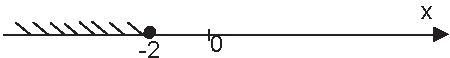Неравенством называется отношение, связывающее два выражения посредством знаков >, <, ⩾, ⩽. Например, x - 1 > 3, x + y > 2x, 1 < 3…
В состав выражений, входящих в неравенство, могут входить переменные.
Значения переменных, при которых неравенство обращается в истинное, называются решениями неравенства. Решить неравенство – это значит найти все его решения.
Два неравенства называются равносильными, если каждое решение первого неравенства является решением второго, и наоборот – каждое решение второго неравенства является решением первого.
Пример:
Неравенства 2x - 1 > 3 и 2x > 4 равносильны, так как все решения первого неравенства являются решениями второго;
Неравенства x - 1 > 3 и x - 1 ⩾ 3 неравносильны, так как не все решения второго неравенства являются решениями первого.
Для того чтобы найти решение неравенства, его заменяют равносильным ему неравенством и решают получившееся.
Пример решения неравенства:
1. Решить неравенство 1 - 2x ⩾ 5.
Перенесем 1 в правую часть:
-2x ⩾ 4;
Разделим левую и правую часть на (-2), помня, что, деля левую и правую часть на отрицательное число нужно менять знак ⩾ на ⩽ и наоборот. Получаем:
x ⩽ -2.
Ответ: x ⩽ -2.
Записать ответ можно было и в таком виде:
x ∈ (-∞; -2].
Иногда бывает полезно изобразить решение неравенства на числовой прямой. Решение этого неравенства будет выглядеть так: