Неравенства вида ![]() решаются по следующей схеме:
решаются по следующей схеме:
1. Находят ОДЗ. Для этого решают неравенство f1(x) ≥ 0.
2. Если стоит знак > или ≥, то ту часть ОДЗ, где f2(x) < 0 сразу принимают в множество решений неравенства, а если < или ≤, то сразу исключают. Чтобы это определить решают неравенство f2(x) < 0 и пересекают полученное решение с ОДЗ.
3. Для той части ОДЗ, где f2(x) ≥ 0 обе части неравенства положительны - можно возводить в квадрат. Возводить обе части неравенства в квадрат можно только тогда, когда обе части положительны. Возведя в квадрат, получим неравенство, найдем его решения, и это множество решений пересечем с ОДЗ. Полученное множество, объединенное с множеством, полученным в пункте 2. будет искомым решением.
Пример:
Решить неравенство ![]()
Решение:
1 Найдем ОДЗ 8x + 4 ≥ 0, x ≥ 0,5
2. Решим неравенство x - 2 < 0, x < 2. Получается, что при x < 2 правая часть отрицательна и неравенство будет истинно для всех x < 2, удовлетворяющих ОДЗ. Действительно, левая часть при этом положительна, а положительное число всегда больше отрицательного. Найдем все такие значения переменной x, найдя пересечение этого множества с ОДЗ.
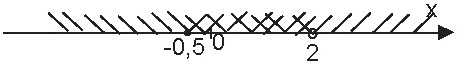
Итак, промежуток [-0,5; 2) будет входить в множество решений неравенства.
3. Если x ≥ 2 - обе части положительны, можно возводить в квадрат, получаем 8x + 4 ≥ (x - 2)2.
Решим это неравенство:
8x + 4 ≥ x2 - 4x + 4;
x2 - 12x ≤ 0;
x(x - 12) ≤ 0.
Решим неравенство методом интервалов.

Получили промежуток [0; 12]. Пересекаем его с промежутком и с ОДЗ.

Получим промежуток [2; 12]
Ответ: [-0,5; 12].

