Арифметической прогрессией называется последовательность чисел, в которой каждый член (начиная со второго) получается из предыдущего путем прибавления к нему одного и того же числа d. Число d называют разностью арифметической прогрессии. Для того, чтобы задать арифметическую прогрессию, нужно задать ее первый член a₁ и разность.

Примеры арифметических прогрессий:

1. 5, 8, 11, 14, 17… . Здесь первый член равен 5, а разность равна 3.

2 . 10, 8, 6, 4, 2, 0, -2… . Здесь первый член равен 10, а разность равна -2.

Итак, первый член прогрессии равен a₁, второй - a₁+d, третий a₁+d+d = a₁+2d, четвертый a₁+2d+d = a₁+3d …. Таким образом, n-й член прогрессии вычисляется по формуле a_n = a₁+(n-1)d.

Утверждение: Сумма n членов арифметической прогрессии вычисляется по формуле

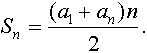
Докажем это утверждение сначала для четных n.

Рассмотрим последовательность a₁, a₁+d, a₁+2d ... a₁+(n-3)d, a₁+(n-2)d, a₁+(n-1)d.

Найдем сумму этой последовательности, группирую слагаемые таким образом: первый член складываем с n-ым, второй с (n-1)-ым, третий с (n-2)-ым, и т. д.

Получим сумму:

S_n = (a₁+a₁+(n-1)d)+(a₁+d+a₁+(n-2)d)+(a₁+2d+a₁+(n-3)d)+ ... = (a₁+a₁+(n-1)d)+(a₁+a₁+d+nd-2d)+(a₁+a₁+2d+nd-3d)+ ... =  (a₁+a₁+(n-1)d)+(a₁+a₁+nd-d)+(a₁+a₁+nd-d)+ ... = (a₁+a₁+(n-1)d)+(a₁+a₁+(n-1)d)+(a₁+a₁+(n-1)d)+ ...

видим, что получились одинаковые слагаемые. Всего таких слагаемых n/2.

Значит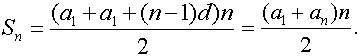  

Докажем теперь это утверждение для нечетных n.

Если n нечетное, значит (n-1)-четное.

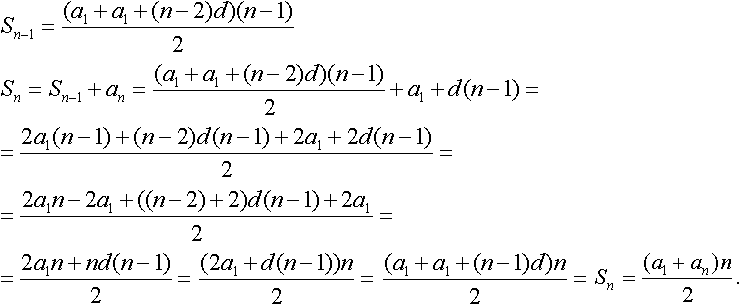
Примеры задач на арифметическую прогрессию.

1.Найдите сумму первых 50 членов арифметической прогрессии, если известно, что a₁=-2, d=3.

Решение.

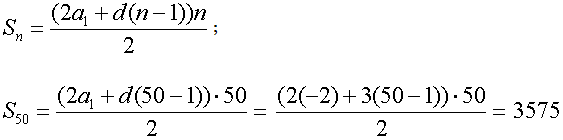
Ответ: 3575.

2. Начинающий пловец первый раз проплыл дистанцию за 1 минуту и 55 секунд. Тренер предполагает, что он будет улучшать результат на 1,5 секунды каждый месяц. С каким результатом пловец проплывет эту же дистанцию через 10 месяцев.

Решение.

В этой задаче мы имеем дело с арифметической прогрессией, в которой a₁ = 1 мин. 55 сек = 115 сек., d = 1,5 сек. Чтобы решить задачу, нам нужно найти 11 член этой прогрессии.

a₁₁ = a₁+(11-1)d = 115-1,5*10 = 100 сек. = 1 мин. 40 сек.

Ответ: 1мин. 40 сек.