Геометрической прогрессией называется последовательность чисел, в которой каждый член (начиная со второго) получается из предыдущего путем умножения его на одного и того же число q ≠ 0. Число q называют знаменателем геометрической прогрессии. Для того, чтобы задать геометрическую прогрессию, нужно задать ее первый член a₁ и знаменатель q.

Геометрическая прогрессия возрастает при q > 1, убывает при 0 < q < 1.

Примеры геометрических прогрессий:

1. 2, 4, 8, 16… . Здесь первый член равен 1, а знаменатель равен 2.

81, 27, 9, 3, 1, 1/3… . Здесь первый член равен 81, а знаменатель равен 1/3.

Итак, первый член прогрессии равен a₁, второй - a₁q, третий a₁q*q = a₁q², четвертый a₁q²*q = a₁q³…. Таким образом, n-й член прогрессии вычисляется по формуле a_n = a₁q^n-1.

Утверждение: Сумма n членов геометрической прогрессии вычисляется по формуле

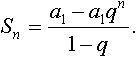
Доказательство.

S_n = a₁+a₁q+a₁q²+a₁q³+...+a₁q^n-1.

Умножим на , получим:

S_nq = a₁q+a₁q²+a₁q³+...a₁qⁿ.

Теперь вычтем S_nq из S_n.

Получим:

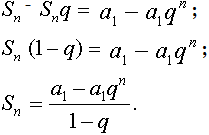
Примеры задач на геометрическую прогрессию.

1. Найдите сумму первых 10 членов геометрической прогрессии, если известно, что a₁ = 3, q = 4.

Решение.

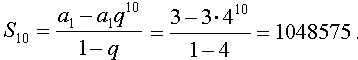
2. За одну минуту биомасса увеличивается в 2 раза. Какой вес она будет иметь через  5 минут, если сейчас ее вес 3 кг.

Решение.

Мы имеем дело с геометрической прогрессией, у которой a₁ = 3, а q = 2 Чтобы решить задачу, нам нужно найти шестой член этой прогрессии.

a₆ = a₁q^6-1 = 3*2^6-1 = 96.

Ответ: 96.