Корни уравнения cos(x) = a, -1 ⩽ a ⩽ 1 выражаются формулой x = ±arcsin(a)+2πn, n ∈ Z.
Примечание: Очевидно, что уравнение cos(x) = a не имеет решений, если а не входит в промежуток [-1;1], то есть |a| ⩽ 1
Попробуем разобраться, почему, решения выражаются этой формулой.
Начертим координатную плоскость и тригонометрическую окружность. Косинус, по определению,- это абцисса точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол а. Начертим множество всех точек, абциссы которых равны а – это будет прямая x = a. Прямая пересечет окружность в двух точках.
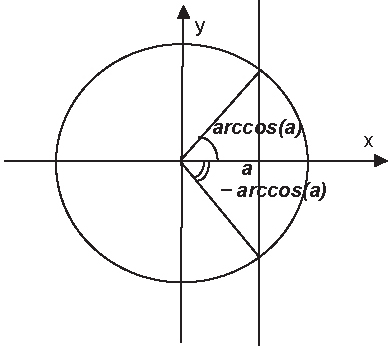
Один из углов, соответствующих этой точке будет иметь величину arccos(a). Этой же точке будет соответствовать и угол arccos(a)+2π, и угол arccos(a)+4π, и угол arccos(a)+6π и т.д.
Все вместе это можно выразить формулой x = arccos(a)+2πn, n ∈ Z.
Один из углов, соответствующих второй точке, будет иметь величину -arccos(a). Этой же точке будет соответствовать и угол -arccos(a)+2π, и угол -arccos(a)+4π, и угол -arccos(a)+6π и т.д.
Все вместе это можно выразить формулой x = -arccos(a)+2πk, k ∈ Z.
Объединение этих двух формул дает формулу x = ±arccos(a)+2πn, n ∈ Z.

