Волны.
Содержание.
1. Основные понятия и определения.
1.1.Определение волны.
1.2. Поперечные волны.
1.3.Продольные волны.
1.4. Фронт волны и волновая поверхность.
1.5. Длина волны.
2. Волновое уравнение.
2.1. Полезные математические сведения. Определение волнового
уравнения.
3. Упругие волны в стержне.
3.1. Волновое уравнение.
4. Упругие волны в газах и жидкостях
4.1 Волновое уравнение.
4.2 Случай идеального газа.
5. Список использованной литературы.
6. Задания для самостоятельной подготовки.
1. Основные понятия и определения.
1.2 Определение волны.
Волной называется процесс распространения колебаний в пространстве. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью v.
В поступательное движение частицы среды, в которой распространяется волна, не вовлекаются. Они просто колеблются около своих положений равновесия.
По направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.
1.2. Поперечные волны.
В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.
Упругие поперечные волны возникают лишь в среде, обладающей сопротивлением сдвигу. Таким образом, в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
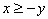
На рис. 1 изображено движение частиц, участвующих в распространении поперечной волны.1, 2 и т. д. - отстоящие друг от друга на расстояние, равное 1/4vТ - на расстояние, проходимое волной за четверть периода колебаний, совершаемых частицами.
Опишем распространение волны, показанной на рис. 1.. В начальный момент времени волна, распространяясь вдоль оси слева направо, достигла частицы 1. Частица начала смещаться из положения равновесия вверх, возбуждая за собой следующие частицы. Через четверть периода частица 1 достигла крайнего верхнего положения, а частица 2только начинала смещаться из положения равновесия. По прошествии еще четверти периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигнет крайнего верхнего положения. И теперь уже третья частица начнет смещаться вверх из положения равновесия. В момент времени, равный Т, первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. Волна к моменту времени T, пройдя путь vТ, достигнет частицы 5.
1.3.Продольные волны.
В продольной волне частицы среды колеблются вдоль направления распространения волны.
Движение частиц при распространении в среде продольной волны показано на рис. 2 . Все приводимые выше рассуждения, касающиеся поведения частиц в поперечной волне, могли быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево. При распространении в среде продольной волны создаются чередующиеся сгущения и разрежения частиц (места сгущения частиц обведены на рисунке пунктиром), которые перемещаются в направлении распространения волны со скоростью v.
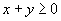
1.4. Фронт волны и волновая поверхность.
На рис. 1 и 2 показаны колебания частиц, положения равновесия которых лежат на оси х. Но колеблются не просто частицы, расположенные вдоль оси х, а совокупность частиц, заключенных в некотором объеме. Волновой процесс, распространяясь от источника колебаний, охватывает все новые и новые части пространства. Совокупность всех точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Волновой поверхностью называют геометрическое место точек, колеблющихся в одинаковой фазе. Волновая поверхность может быть проведена через любую точку пространства, охваченного волновым процессом - волновых поверхностей существует бесконечное множество, в то время как волновой фронт каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается.
Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер.
1.5. Длина волны.
Рассмотрим распространение плоской волны вдоль оси х. Все точки среды, положения равновесия которых имеют одинаковую координату х ,но различные значения координат y и z, колеблются в одинаковой фазе.
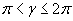
На рис. 3 показана кривая, которая дает смещение ![]() из положения равновесия точек с различными x в некоторый момент времени. На рисунке показан график функции
из положения равновесия точек с различными x в некоторый момент времени. На рисунке показан график функции ![]() (х, t) для некоторого фиксированного момента времени t. С течением времени график перемещается вдоль оси х. Такой график можно строить как для продольной, так и для поперечной волны. В обоих случаях он выглядит одинаково.
(х, t) для некоторого фиксированного момента времени t. С течением времени график перемещается вдоль оси х. Такой график можно строить как для продольной, так и для поперечной волны. В обоих случаях он выглядит одинаково.
Расстояние ![]() , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что
, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. Очевидно, что
![]() =vТ, (1.1)
=vТ, (1.1)
где v – скорость волны, Т – период колебаний.
Длина волны - расстояние между ближайшими точками среды, колеблющимися с разностью фаз, равной 2П. Заменив в соотношении (1.1) Т через 1/![]() (
(![]() – частота колебаний), получим
– частота колебаний), получим
![]()
![]() =v (1.2)
=v (1.2)
Рассмотрев кратко основные понятия, связанные с волной, перейдем к описательной стороне, т.е. волновому уравнению.
2. Волновое уравнение.
2.1. Полезные математические сведения. Определение волнового уравнения.
Рассмотрим произвольную функцию f(at-bx) (2.3) от аргумента аt—bх. Продифференцировав ее дважды по t получим:
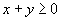 (2.4)
(2.4)
Здесь штрих означает дифференцирование по аргументу at—bx.
Продифференцировав теперь нашу функцию дважды по х получим:
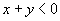 (2.5)
(2.5)
Сравнив (2.4) и (2.5), нетрудно заметить, что функция (2.3) удовлетворяет уравнению
![]() (2.6)
(2.6)
где
u=a/b.
Этому же уравнению удовлетворяет произвольная функция
f(at+bx) (2.7) (2.7) аргумента at+bx, а также сумма функций вида (2.3) и (2.7).
Функции (2.3) и (2.7) изображают при положительных a, b плоские волны, распространяющиеся, не деформируясь, со скоростью и в сторону соответственно возрастающих или убывающих значений х **).
Уравнение (2.6)—дифференциальное уравнение в частных производных, играющее в физике очень важную роль, называется волновым уравнением. Оно не имеет решений, отличных от тех, которые могут быть представлены функциями вида (2.3) и (2.7) или суперпозицией таких функций, например,
f1(at - bх) + f2(at+bx).
Если можно доказать, что та или иная физическая величина s удовлетворяет уравнению вида
![]() (2.6а)
(2.6а)
можно на основании рассмотренных математических сведений заключить, что процесс изменений этой величины носит характер плоской, волны - распространяющейся в ту или другую сторону со скоростью и, или суперпозиции таких волн.
Вид функций f1, f2 определяется характером движения источника волн, а также явлениями, происходящими на границе среды.
Допустим, источником волн является плоскость х=0, на этой плоскости величина S колеблется но закону s =Acoswt. Тогда от плоскости х=0 распространяются вправо и влево волны
s= Acos(wt![]() kx), k =
kx), k =![]() .
.
Так как волновое уравнение линейное, если ему удовлетворяют функции s1, s2,s3, ... в отдельности, то ему удовлетворяет также функция
S == S1 + S2 + S3 + ...
(принцип, суперпозиции).
Рассмотрим следующие примеры.
а) Волновому уравнению удовлетворяют синусоидальные бегущие волны
s1 = Aсоs(wt — kx),s2= Acos(wt+kx).
На основании принципа суперпозиции волновому уравнению удовлетворяет стоячая волна
s=2Acoskx coswt
являющаяся суперпозицией только что рассмотренных синусоидальных бегущих волн.
б) Волновому уравнению на основании принципа суперпозиции удовлетворяет всякая функция вида
S=![]()
Это—функция вида f(at—bx); она изображает несинусоидальную волну, распространяющуюся без деформации в сторону возрастающих х.
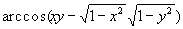
в) Пусть волны S1, S2, имеющие вид коротких импульсов, распространяются навстречу одна другой. В некоторый момент моментальный снимок суперпозиции S1 + S2 этих волн имеет вид, показанный на рис. 4,а. Через некоторое время моментальный снимок волны будет иметь вид, показанный на рис. 4, б, – волны пройдут “одна сквозь другую” и притом каждая так, как будто другой не существует.
3. Упругие волны в стержне.
3.1. Волновое уравнение.
На примере распространения упругих волн в стержне, рассмотрим как работает математический аппарат волнового уравнения, описанный выше.
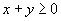
Испльзуем второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+![]() х. Масса его р0S0
х. Масса его р0S0![]() х, где р0 иS0 – соответственно плотность и сечение в отсутствие деформации.
х, где р0 иS0 – соответственно плотность и сечение в отсутствие деформации. ![]() – смещение центра тяжести рассматриваемого куска. Тогда
– смещение центра тяжести рассматриваемого куска. Тогда
![]()
слева стоит произведение массы куска на ускорение д2![]() /дt2его центра тяжести, справа – результирующая внешних сил, действующая на кусок.
/дt2его центра тяжести, справа – результирующая внешних сил, действующая на кусок.
Разделим уравнение на S0![]() :
:
![]() (2.7)
(2.7)
Перейдя к пределу при ![]() , получим уравнение
, получим уравнение
![]() (2.8)
(2.8)
справедливое в каждой точке стержня. Получили, что ускорение данной точки пропорционально частной производной напряжения по ж в этой точке.
Подставляя в (2.8) соотношение (2.7), получим:
![]() (2.9)
(2.9)
Используя определение деформации, получаем:
![]() (2.10)
(2.10)
Это—волновое уравнение.Оно показывает, что смещение распространяется но стержню в виде волн
![]() (2.11)
(2.11)
или образует суперпозицию таких волн. Скорость распространения этих волн (скорость звука в стержне)
![]() (2.12)
(2.12)
(мы опускаем для краткости индекс 0 у р). Эта скорость тем больше, чем жестче и чем легче материал. Формула (2.12)—одна из основных формул акустики.
Определим скорость v =![]() , с которой движутся отдельные плоскости х = const (не смешивать с u), деформацию
, с которой движутся отдельные плоскости х = const (не смешивать с u), деформацию ![]() инапряжение
инапряжение ![]() . Дифференцируя (2.11)по t и но x,получаем:
. Дифференцируя (2.11)по t и но x,получаем:
v=![]() uf’(x
uf’(x![]() ut) (2.13a)
ut) (2.13a)
![]() =f"(x
=f"(x ![]() ut), (2.13б)
ut), (2.13б)
![]() =Ef’ (x
=Ef’ (x ![]() ut). (2.13в)
ut). (2.13в)
Таким образом, смещение, скорость, деформация и напряжение распространяются в виде связанных определенным образом между собой недеформирующихся волн, имеющих одну и ту же скорость и одинаковое направление распространения.
На рис. 5 показаны “моментальные снимки”, относящиеся к одним и тем же моменту времени, смещению, деформации и скорости в одной и той же упругой волне. Там, где смещение имеет максимум или минимум, деформация и скорость равны нулю, так как они обе пропорциональны производной f"{x ![]() ut). Около максимума или минимума смещения соседние (бесконечно близкие) точки одинаково смещены и, следовательно, нет ни растяжения, ни сжатия; в тот момент, когда смещение достигает максимума (минимума), его возрастание сменяется убыванием (или наоборот).
ut). Около максимума или минимума смещения соседние (бесконечно близкие) точки одинаково смещены и, следовательно, нет ни растяжения, ни сжатия; в тот момент, когда смещение достигает максимума (минимума), его возрастание сменяется убыванием (или наоборот).
Сравнивая формулы (2.13а), (2.13в) и принимая во внимание (2.12) мы видим, что
![]() (2.14)
(2.14)
где
![]() (2.15)
(2.15)
есть величина, не зависящая от вида функции f и целиком определяемая свойствами материала. Эта величина называется удельным акустическим сопротивлением материала. Она является, как мы видим, наряду с u его важнейшей акустической характеристикой. Название величины ![]() связано с формальной аналогией между уравнениями (2.14) и законом Ома (р аналогично разности потенциалов, v - силе тока).
связано с формальной аналогией между уравнениями (2.14) и законом Ома (р аналогично разности потенциалов, v - силе тока).
4.. Упругие волны в газах и жидкостях
4.1. Волновое уравнение.
Рассмотрим газ или жидкость как сплошную непрерывную среду, отвлекаясь от его атомистической структуры. Смещением ![]() - общее смещение вещества, заполняющего объем, заключающий в себе очень много атомов, но малый по сравнению с длиной волны.
- общее смещение вещества, заполняющего объем, заключающий в себе очень много атомов, но малый по сравнению с длиной волны.
Предположим, что рассматриваемый газ или жидкость находятся в очень длинной цилиндрической трубе, с образующими, параллельными оси х, и смещение зависит только от координаты х. Применить к столбу газа или жидкости, заполняющему трубу, те же рассуждения, что и к стержню и придём, таким образом, к уравнению
![]() (2.16)
(2.16)
где р = —![]() есть давление в газе или жидкости. Здесь
есть давление в газе или жидкости. Здесь ![]() — значение плотности в состоянии равновесия. Пусть ей соответствует давление р0. Величины р0,
— значение плотности в состоянии равновесия. Пусть ей соответствует давление р0. Величины р0, ![]() не зависят ни от х, ни от t.
не зависят ни от х, ни от t.
Уравнение (2.16) применимо и в случае плоских волн в неограниченной жидкой или газообразной среде (можно мысленно выделить цилиндрический столб, параллельный направлению распространения и применить к нему те же рассуждения, что к столбу, заключенному в трубе).
р - функция плотности данной массы газа (или жидкости) и ее температуры. Температура в свою очередь изменяется при сжатии и разрежении. Теплопроводность газов и жидкостей очень мала, поэтому можно считать, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит без заметного теплообмена с соседними частями - адиабатически. В термодинамике в этом случае (если можно пренебречь внутренним трением и некоторыми другими явлениями) температура является однозначной функцией плотности, и давление также.
При заданной деформации ![]() в твердом теле также зависит от температуры. Но в акустике твердых тел это обстоятельство не играет, существенной роли.
в твердом теле также зависит от температуры. Но в акустике твердых тел это обстоятельство не играет, существенной роли.
В газах и в жидкостях за некоторыми исключениями (например вода, при температуре ниже 4° С) температура растет при сжатии и уменьшается при расширении.
Есть однозначная функция плотности:
p=f(p). (2.17)
Введем обозначения
![]() , (2.18) где
, (2.18) где ![]() и
и ![]() — соответственно изменения давления и плотности при нарушении равновесия.
— соответственно изменения давления и плотности при нарушении равновесия.
Подставляя первую формулу (2.18) в (2.16) и принимая во внимание, что при равновесии давление не зависит от х, т. е.
![]()
получаем:
![]() (2.19)
(2.19)
Определим теперь связь между ![]() и деформацией
и деформацией ![]() =
=![]() . Мы сначала выразим
. Мы сначала выразим![]() через
через ![]() , а затем
, а затем ![]() через
через ![]() :
:
а) Подставляя (6.28) в (6.27), имеем:
P0+![]() =f(
=f(![]() +
+![]() )
)
разлагая f(![]() +
+![]() ) в ряд по степеням
) в ряд по степеням ![]() ,
,
P0+![]() =f(
=f(![]() )+f’(
)+f’(![]() )
)![]() +1/2f’(
+1/2f’(![]() )(
)(![]() )2......
)2......
Так как P0=f(![]() ), то получаем:
), то получаем:
![]() =f’(
=f’(![]() )
)![]() +1/2f’’(
+1/2f’’(![]() )(
)(![]() )2..... (2.20)
)2..... (2.20)
Считаем уплотнения и разрежения настолько малыми, что допустимо пренебречь в разложении (2.20) членами, пропорциональными (![]() )2, (
)2, (![]() )3, . . ., и заменить (2.20) линейным соотношением
)3, . . ., и заменить (2.20) линейным соотношением
![]() =f’(
=f’(![]() )
)![]()
Таким образом мы исследуем волны малой интенсивности.
f’(![]() ) —постоянный при данных условиях опыта коэффициент, определяемый состоянием среды при равновесии.
) —постоянный при данных условиях опыта коэффициент, определяемый состоянием среды при равновесии.
б) Объем V0 в результате деформации превращается в объем
V=V0 (1+![]() ), (2.21)
), (2.21)
так как здесь поперечный размер (в отличие от твердого стержня) остается, постоянным, а длина превращается в . Но произведение плотности на объем, равное массе рассматриваемой порции вещества, не меняется:
Подставляя (2.18) и (2.21), получаем:
Пренебрегая и здесь высшими степенями малой величины , получаем:
Таким образом,
(2.22)
Подставляя, наконец, (2.22) в (2.19), мы получаем волновое уравнение
(2.23)
(2.24)
Следовательно, рассматриваемые малые деформации распространяются в виде плоских не деформирующихся волн; скорость распространения (скорость звука) тем больше, чем сильное в данной среде возрастает давление при адиабатическом возрастании плотности; она раина квадратному корню из производной давления по плотности, взятой при значении последней в отсутствие волны ( ).
4.2. Случай идеального газа.
Идеальным газом называется газ, для которого справедливо уравнение состояния
pV=RT, (2.25)
где p – давление, V—объем одного моля, R—универсальная газовая постоянная, равная 8,3143 эрг/град, T—температура, измеренная по термодинамической шкале (“абсолютная температура”), или
где М— масса 1 моля, = M/V— плотность.
Воздух, кислород, азот, водород и многие другие газы при комнатной температуре и давлении порядка атмосферного можно рассматривать с достаточным для акустики приближением как идеальные газы.
В случае идеального газа соотношение (2.17) имеет вид
(2.26)
где
постоянная величина (С и С — теплоемкости газа соответственно при постоянном давлении и постоянном объеме). Следовательно, здесь
(2.27)
(формула Лапласа).
Еще задолго до Лапласа вопросом о скорости звука в воздухе занимался Ньютон. Он считал, что
(2.26а)
т. е. не учитывал изменения температуры воздуха при распространении в нем звуковой волны, вследствие чего получил для скорости звука соотношение
(2.27а)
Это соотношение можно получить из уравнения (2.24), подставляя в него (2.26а) вместо (2.26).
Для воздуха ( =1,4) при комнатной температуре (20° С, Т =293°) формула Ньютона дает u =290 м/сек, формула Лапласа и =340 м/сек. Сравнивая эти значения с теми, которые дает опыт (гл. V, § 3), мы видим, что формула Лапласа, в отличие от формулы Ньютона, хорошо согласуется с опытом. Формула Лапласа хорошо подтверждается на опыте и для других газов (но крайней мере при не очень высоких частотах.
Этим оправдывается предположение о том, что сжатие и разрежение газа в звуковой волне являются практически адиабатическими процессами.
5. Список использованной литературы.
6. Задания для самостоятельной подготовки.
Задача №1.
Амплитуда вынужденных колебаний реактора при очень малой частоте 2 мм, а при резонансе 16 мм. Предполагая, что декремент затухания меньше единицы, определить его.
Задача №2.
Две волны Х1=Аsin(wt-kl) и Х2=Аsin(wt+kl) с одинаковыми частотами 4Гц распространяются со v=960 см/сек. Они интерферируют между собой и образуют стоячую волну. Определить амплитуды точек стоячей волны через каждые 20 см, начиная отсчет от узла. Определить величину смещения и скорость этих точек для момента времени 7/24 сек.
Задача №3.
Между приемником и стенкой расположен источник звуковых колебаний с частотой – 100 Гц. Линия, проведенная через приемник и источник, нормальна к стенке, которая движется к источнику вдоль этой линии со v=7 м/с. Скорость звука 340 м/с. Возможно ли возникновение акустического биения.

