Замечательные кривые.

План.

Прямая и окружность.

Циклоида.

Кривая кратчайшего спуска.

Эллипс.

Архимедова спираль.

Архимедовы задачи.

Логарифмическая спираль.

Теорема Паскаля.

Теорема Брианшона- теорема -перевёртыш.

Лемниската Бернулли.

Список литературы

Прямая и окружность.

Прямая и окружность - две самые простые и, несмотря на это, замечательные по своим свойствам кривые. Любой человек знаком и с прямой и с окружностью, но вместе с тем незнаком и с малой частью их удивительных свойств. Например, не каждому известно, что если вершины двух треугольников АВС и A"B"C" лежат на трех прямых, которые пересекающихся в одной точке 5 (рис. 1), то тогда три точки пересечения сторон треугольников АВ с А"В", ВС с В"С" и АС с А"С"- точки М, К, L соответственно, находятся на одной и той же прямой!

Рис. 1, 2.

Легко догадаться, что если точка М, движущаяся по плоскости, остаётся на равных расстояниях от двух неподвижных точек F₁ и F₂ той же плоскости, то есть движется так, что MF₁= MF₂, то можно утверждать, что она описывает прямую (рис. 2).

А какую кривую опишет точка М, если ее расстояние до точки F₁ будет в определенное число раз превосходить расстояние до точки F₂ (например, вдвое, как на рис. 3). ДА-ДА - окружность. Следовательно, если точка М движется по плоскости так, что ее расстояние до одной из двух неподвижных точек F₁ и F₂ плоскости будет изменяться пропорционально расстоянию до другой точки MF₁ = k MF₂, то она будет описывать либо прямую (когда коэффициент пропорциональности k равен единице), либо окружность (в случае, когда коэффициент пропорциональности отличен от единицы).

Рис. 3.

Рис. 4.

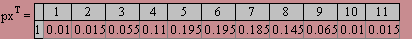
Циклоида.

Приложите к нижнему краю классной доски линейку и катите по ней обруч или круг (картонный или деревянный), прижимая его к линейке и к доске. Если прикрепить к обручу или кругу в точке соприкосновения его с линейкой кусок мела, то мел вычертит кривую (рис. 5), которая называется циклоидой. Циклоида по-гречески значит “кругообразная”.

Рис. 5.

Одному обороту обруча соответствует одна “арка” циклоиды MM"M""N", если обруч будет катиться дальше, то будут получаться еще и еще арки той же циклоиды.

Для того, чтобы построить на бумаге приближенно одну арку циклоиды, описанную при качении обруча диаметром, равным, например, трем сантиметрам, необходимо отложить на прямой отрезок, равный 3х3,14 = 9,42 см.

Тогда получится отрезок, длина которого равна длине обода обруча, т. е. длине окружности диаметром в три сантиметра. Разделим далее этот отрезок на некоторое число равных частей, например на 6, и для каждой точки деления изобразим наш обруч в том его положении, когда он опирается именно на данную точку (рис. 6), занумеровав эти положения цифрами:

О, 1, 2, 3, 4, 5, 6.

Чтобы перейти из одного положения в соседнее, обруч нужно повернуть на одну шестую полного оборота, потому что расстояние между соседними точками деления равно шестой части окружности. Так, если в положении 0 мел будет находиться в точке М₀, то в положении 1 он будет лежать в точке M₁ - на одной шестой окружности от точки касания, в положении 2 - в точке М₂ - на две шестых от точки касания и т. д. Чтобы получить точки M₁, M₂, М₃ и т.д., нужно лишь производить отметки соответствующей окружности, начиная от точки касания, радиусом, равным 1,5 см, причем в положении 1 нужна одна засечка, в положении 2 - две засечки, выполненные одна за другой, в положении 3 - три засечки и т. д. Теперь для вычерчивания циклоиды остается соединить точки

М₀, M₁, М₂, М₃, M₄, M₅, M₆

плавной кривой (на глаз).

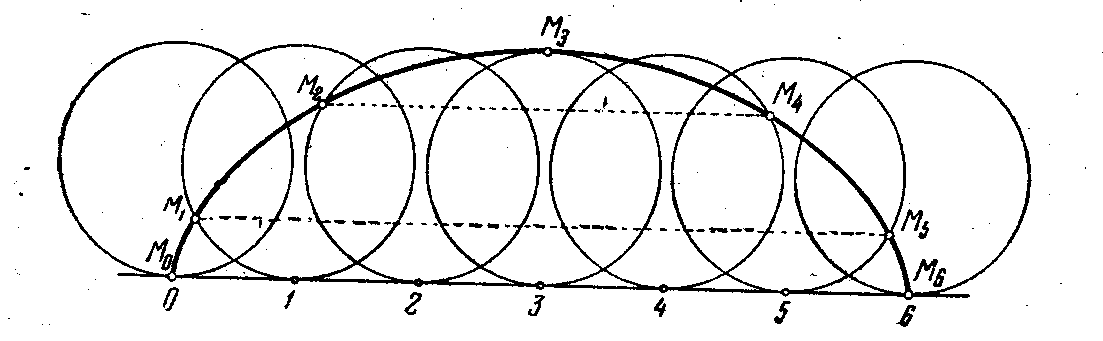
Рис. 6.

Кривая кратчайшего спуска.

Нельзя не отметить ещё одно из замечательных свойств циклоиды.

Постараемся ответить на такой вопрос: какую форму следует придать хорошо отшлифованному металлическому желобу, соединяющему две заданные точки А и В (рис. 7.), чтобы полированный металлический шарик скатывался по этому желобу из точки А в точку В за кратчайшее время? Думаете, что нужно остановитьсяна прямолинейном желобе, так как только вдоль него шарик пройдет кратчайший путь от А до В? Но ведь речь идет не о кратчайшем пути, а о кратчайшем времени, время, как известно, зависит не только от длины пути, но и от скорости, с которой бежит шарик. Так, если желоб прогнуть вниз, то его часть, начиная от точки А, будет круче опускаться вниз, чем в случае прямолинейного желоба, и шарик, падая по нему, приобретет скорость большую, чем на участке такой же длины прямолинейного желоба.

Рис. 7.

Но если сделать начальную часть очень крутой и сравнительно длинной, то тогда часть, примыкающая к точке В, будет очень пологой и также сравнительно длинной. Первую часть шарик пройдет быстро, вторую очень медленно и может запоздать с приходом в заданную точку В. Видимо, желобу нужно придавать вогнутую форму, но делать выгиб не слишком значительным.

Рис. 8.

Итальянский физик и астроном Галилей и братья Бернулли тоже однажды задумались над этой задачей. Галилей решил, что желоб, для достижения кратчайшего времени нужно выгибать по дуге окружности. Но швейцарские математики около трехсот лет тому назад точным расчетом доказали, что это не верно. Желоб нужно выгибать по дуге циклоиды, опрокинутойвниз (рис. 8).

С тех пор за это свойство циклоида получила громко звучащее мудреное название: “брахистохрона”. Оно составлено из двух греческих слов, означающих “кратчайший” и “время”.

А доказательства Бернулли послужили, началом новой отрасли математики - вариационного исчисления, которая занимается отысканием вида кривых, для которых та или иная интересующая нас величина достигает своего наименьшего (а в некоторых вопросах - наибольшего) значения.

Эллипс.

Пусть точка М движется в плоскости так, что сумма расстояний этой точки до двух неподвижных точек F₁ и F₂ на этой плоскости остается неизменной. Концы нити привяжем к двум булавкам и воткнем эти булавки в лист бумаги, оставляя сначала нить ненатянутой. Если оттянуть теперь нить с помощью вертикально поставленного карандаша и затем передвигать карандаш, слегка придавливая его к бумаге и следя за тем, чтобы нить была натянутой (рис. 4), то острие М карандаша опишет кривую овальной формы (похожую на сплющенный круг), которая называется эллипсом.

Если хотите получить полный эллипс, нужно перекинуть нить на другую сторону от булавок, после того как будет описана одна половина эллипса. Нетрудно догадаться, что сумма расстояний от острия М карандаша до булавочных проколов F₁ и F₂ остаётся неизменной во все время движения. Можете проверить, что эта сумма равна длине нити.

Рис. 9.

Проколы булавок отмечают на бумаге две точки, называемые фокусами эллипса. Слово фокус в переводе с латинского означает “очаг”, “огонь”; оно оправдывается следующим замечательным свойством эллипса.

Если изогнуть узкую полоску хорошо отполированного металла по дуге эллипса и поместить точечный источник света (“огонь”) в одном фокусе, то лучи света, отразившись от полоски, соберутся в другом фокусе; поэтому и во втором фокусе будет также виден “огонь” - изображение первого (рис. 9.).

Архимедова спираль.

Представьте себе бесконечно длинную секундную стрелку, по которой, начиная от центра циферблата, неутомимо бежит маленький жучок с некоторой постоянной скоростью v см/с. Через минуту жучок будет на расстоянии 60v см от центра, через две - 120v и т.д. Так через t секунд после начала пробега расстояние жучка от центра будет равно vt см.

Так как за одну секунду стрелка успевает повернуться на угол 360°:60 = 6°. за время t она повернется на угол, содержащий 6 t° . А положение жучка на плоскости циферблата через любое число t секунд после начала движения можнл определить следующим образом. Необходимо отложить от начального положения стрелки в направлении ее вращения угол а, содержащий 6t°, и отмерить от центра вдоль нового положения стрелки расстояние r = vt см. Тут мы и настигнем жучка (рис. 10.).

Рис. 10.

Соотношение между углом поворота a стрелки (в градусах) и пройденным расстоянием r (в сантиметрах): r = (va)/6

То есть, r прямо пропорционально a, с коэффициентом пропорциональности k = v/6.

Прикрепим к нашему жучку баночку с черной краской и предположим, что краска, вытекая через крошечное отверстие, оставляет на бумаге след от уносимого вместе со стрелкой жучка.

Тогда на бумаге будет постепенно вырисовываться кривая, которой впервые заинтересовался Архимед в 287 - 212 до н.э.. Поэтому её и назвали спиралью Архимеда. У Архимеда, есественно, не было речи ни о секундной стрелке (тогда и часов с пружиной не было: их изобрели только в XVII в.), ни о жучке. Нам они нужны только для наглядности.

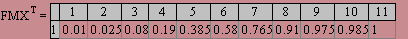
Рис. 11. Рис. 12.

Итак, спираль Архимеда состоит из бесконечно многих витков, начинается в центре циферблата, и все более и более удаляется от него по мере того, как растет число оборотов. На рис. 12 изображены первый виток и часть второго.

С помощью циркуля и линейки невозможно разделить на три равные части наудачу взятый угол (в частных случаях, когда угол содержит, например, 180°, 135° или 90°, эта задача легко решается), а вот если научиться использовать для этого аккуратно нарисованную архимедову спираль, то любой угол можно будет разделить на какое угодно число равных частей.

Попробуем решить следующую задачу: разделим, угол АОВ на три равные части (рис. 12.). Предположим, что стрелка повернулась как раз на этот угол, тогда жучок, будет находиться в точке N на стороне угла. Но когда угол поворота был втрое меньше, то и жучок был втрое ближе к центру О. Чтобы найти это его положение, разделим с помощью циркуля и линейки сначала отрезок ON на три равные части. Получим отрезок ON₁, длина которого втрое меньше, чем ON. Чтобы вернуть жучка на спираль, нужно сделать засечку этой кривой радиусом ON₁ (снова циркуль!). Получим точку М. Угол АОМ и будет втрое меньше угла AON.

Архимедовы задачи.

Однако Архимеда занимали, в большей степени, другие, более трудные и интересные задачи, которые он сам поставил и решил:

1. найти площадь фигуры, ограниченной первым витком спирали (на рис. 11. она заштрихована);
2. получить способ построения касательной к спирали в какой-либо ее точке N.

Обе задачи представляют собой самые ранние примеры задач, относящихся к математическому анализу. Только с XVII в., площади фигур математики начали вычислять с помощью интеграла, а касательные проводить с помощью производных. Поэтому Архимеда часто называют предшественником математического анализа.

Для первой задачи мы просто познакомимся с результатом, полученным Архимедом: площадь фигуры составляет точно 1/3 площади круга радиуса О А.

А для второй задачи покажем ход ее решения, несколько упростив рассуждения самого Архимеда. Скорость, с которой жучок описывает спираль, в каждой точке N направлена по касательной к спирали в этой точке. Если будем знать, как направлена эта скорость, то нетрудно и касательную построить.

Однако движение жучка в точке N складывается из двух различных движений (рис. 13.). Одно из них - по направлению стрелки со скоростью v см/с, а другое - вращательное по окружности с центром в О и радиусом ОN. Допустим, что жучок замер на мгновенье в точке N, тогда он будет уноситься вместе со стрелкой по окружности радиуса ON. Естественно, что скорость последнего вращательного движения направлена по касательной к окружности, но какова ее величина? Если бы жучок мог описать полную окружность радиуса ON, то за 60 секунд он проделал бы путь, равный 2л ON А так как скорость при этом оставалась бы постоянной по величине, то для ее отыскания необходимо разделить путь на время, получим:

(2 л ON)/60 = ( л ON)/30 [см/с] , т. е. немногим более, чем:

0,1ON [см/с] ( л /30 3,14/30 0,105).

Мы теперь знаем обе составляющие скорости в точке N: одну по направлению ON, равную v см/с, и другую, к ней перпендикулярную, равную

( л ON)/30 см/с. Остается сложить их, используя правило параллелограмма. Диагональ полученного параллелограмма представит скорость составного движения к и вместе с тем определит направление касательной NT к спирали в данной точке.

Логарифмическая спираль.

Впервые об этой кривой говорится в одном из писем Декарта в 1638 г. Но более подробное изучение ее свойств было проведено только полвека спустя Якобом Бернулли. На современных ему математиков эти свойства произвели сильное впечатление, а на каменной плите, водруженной намогиле этого знаменитого математика, изобразили витки логарифмической спирали.

Из выше сказанного архимедову спираль описывает точка, движущаяся вдоль луча (“бесконечной стрелки”), а расстояние от начала луча возрастает пропорционально углу его поворота: r = ka. Логарифмическая спираль получается, если не само расстояние, а его логарифм возрастает прямо пропорционально углу поворота. Обычно уравнение логарифмической спирали записывают, пользуясь в качестве основания системы логарифмов неперовым числом е. Такой логарифм числа r называют натуральным логарифмом и обозначают ln r. Итак, уравнение логарифмической спирали записывается в виде ln r = ka

Угол поворота а, естественно, можно измерять по-прежнему в градусах., но математики считают более удобным измерять его в радианах - принимать за меру угла отношение длины дуги окружности между сторонами центрального угла к радиусу этой окружности. Тогда поворот стрелки на прямой угол будет измеряться числом л 1,57, поворот на величину развернутого угла - числом л 3,14, а полный поворот, измеряемый в градусах числом 360, в радианах будет измеряться числом 2 л 6,28.

Рис. 13.

Из многих свойств логарифмической спирали, стоит отметить одно: любой луч, выходящий из начала, пересекает любой виток спирали под одним и тем же углом. Величина этого угла зависит только от числа k в уравнении спирали. При этом под углом между лучом и спиралью понимается угол между этим лучом и касательной к спирали, проведенной в точке пересечения (Рис. 13).

Теорема Паскаля.

Когда Паскаль (1623—1662) открыл замечательное общее свойство конических сечений, ему не было еще и 17 лет. Об этом открытии математикам поведала афиша, отпечатанная в количестве 50 экземпляров. Два из них дошли до нашего времени. Несколько таких афиш были расклеены на стенах домов и церквей Парижа.

Тогда (1640 г.) еще не было научных журналов, на страницах которых можно было бы рассказывать другим ученым о своем открытии. Такие журналы появились лишь четверть века спустя, почти одновременно во Франции и Англии.

Афиша Паскаля и была напечатана на французском языке, а не на латинском, как это было тогда принято. Парижане, глазея на нее, вряд ли могли понять, о чем там идет речь, потому что гениальный автор сжато без доказательств и пояснений излагал свои мысли.

После трех определений в начала афиши шла под названием “леммы 1” теорема, которую мы сегодня, к сожалению, принято формулировать другими словами.

Отметим на окружности шесть точек, перенумерованные в любом порядке (не обязательно в том, в каком они расположены на окружности) и соединим их отрезками прямых. Последний из этих отрезков свяжет шестую точку с первой (рис. 14). По теорема Паскаля три точки пересечения прямых, полученных продолжением этих шести отрезков, взятых через две: первой с четвертой, второй с пятой и третьей с шестой, будут лежать на одной и той же прямой.

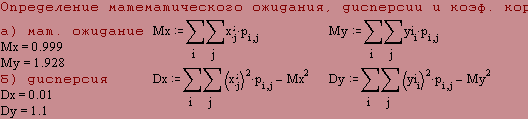
Рис. 14.

Если есть желание, можете сами сделать несколько опытов, разбрасывая по-разному точки на окружности (рис. 15).

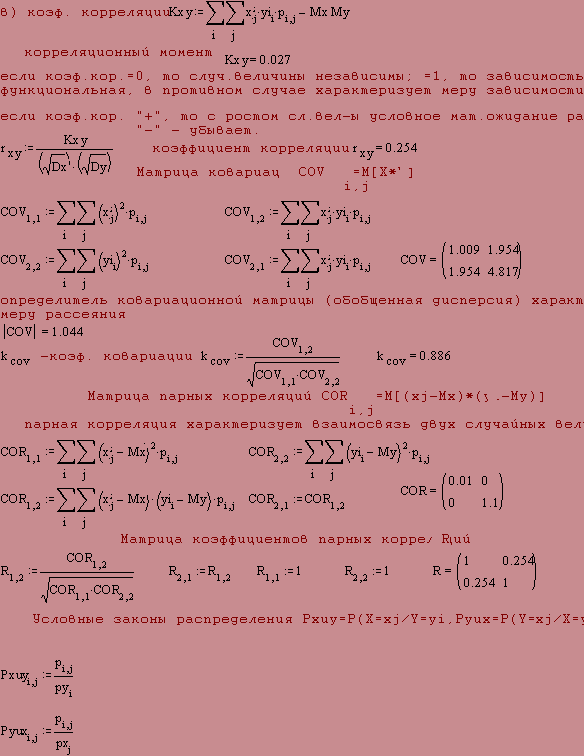
Рис. 15.

Может получиться, что какие-либо прямые, пересечение которых вы ищете, например, первая и четвертая, окажутся параллельными. В этом случае теорему Паскаля нужно понимать так, что прямая, соединяющая две другие точки пересечения, параллельна указанным прямым (рис. 16).

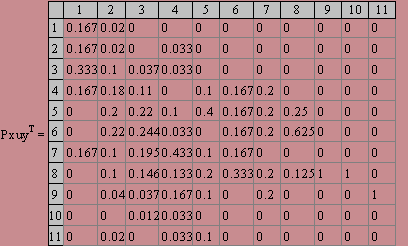
Рис. 16.

Ну а если вдруг вдобавок окажутся параллельными между собой и вторая прямая с пятой, то в этом специальном случае, теорема Паскаля утверждает, что и прямые последней пары - третья и шестая - окажутся параллельными.

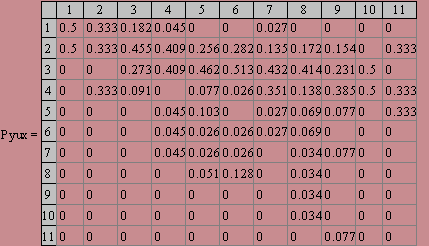
Рис. 17.

Так получается в случае, когда точки на окружности являются вершинами правильного вписанного шестиугольника, перенумерованными в порядке следования на окружности (рис. 17).

Паскаль не ограничился тем, что сформулировал свою теорему для окружности. Он заметил, что она должна оставаться верной, если вместо окружности взять любое коническое сечение: эллипс, параболу или гиперболу. На рис. 18 приведена иллюстрация к теореме Паскаля для случая параболы.

Рис. 18.

Теорема Брианшона- теорема -перевёртыш.

Французский математик Шарль Брианшон (1783— 1864) обнаружил в 1806 г., что теорема, которая, является своего рода перевертышем по отношению к теореме Паскаля.

Рассмотрим следующий пример. Проведем 6 касательных к окружности (или к любому коническому сечению), перенумеруем их в любом порядке и найдем последовательные точки пересечения (рис. 19).

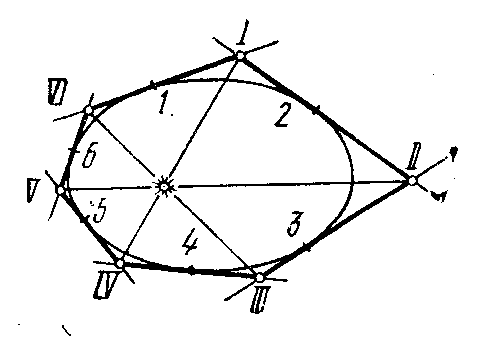
Рис. 19.

Теорема Брианшона утверждает, что три прямых, соединяющих шесть точек пересечения, взятых через две: первой с четвертой, второй с пятой, третьей с шестой, пересекаются в одной точке.

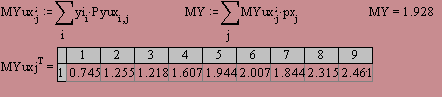
Рис. 20.

Чтобы подчеркнуть тесную связь между формулировками двух теорем, Брианшон записал обе формулировки в двух столбцах, одну против другой (следите за рис. 20, где слева пояснена теорема Паскаля, а справа - Брианшона).

Видно, что для перехода от одной формулировки к другой достаточно произвести некоторые замены одних слов и выражений на другие: вместо точек - касательные, вместо “соединять точки прямыми” - “находить точки пересечения прямых”, вместо “три точки лежат на одной прямой” - “три прямые пересекаются в одной точке”. При этом переходе прямые и точки меняются между собой ролями.

В проективной геометрии существуют условия, при которых в результате подобной замены из одной верной теоремы (не обязательно теоремы Паскаля) получается другая теорема, также верная. Это так называемый принцип двойственности, позволяющий доказывать из двух геометрических теорем только одну, а другая будет верной, так сказать, автоматически.

Лемниската Бернулли.

Рассмотрим кривую, описываемую точкой М на плоскости так, что остается неизменным произведение р расстояний этой точки до двух определенных точек F₁ и F₂ той же плоскости. Эта кривая называется лемнискатой. Лемниската по-гречески значит “ленточная”.

Если длина отрезка F₁F₂ есть с, то расстояния от середины О отрезка F₁F₂ до F1 и F2 равны с/2 и произведение этих расстояний равно – с²/4. Потребуем , чтобы величина р неизменного произведения равнялась как раз с²/4; тогда точка О будет лежать на лемнискате, а сама лемниската будет иметь вид “лежащей восьмерки” (рис. 21). Если продолжить отрезок F₁F₂ в обе стороны

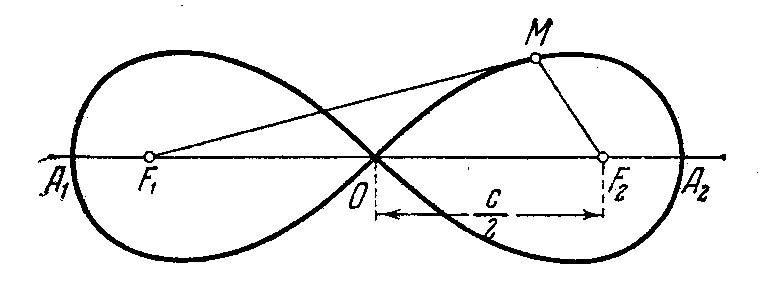
Рис. 21

Продолжив отрезок F₁F₂ в обе стороны до пересечения с лемнискатой, получим две точки А₁ и А₂. Выразим расстояние между А₁А₂= х через известное расстояние с:

(х/2+с/2)(х/2-с/2)=х²/4-с²/4.

Если величину неизменного произведения р взять не равной с²/4, то лемниската изменит свой вид. И при р меньше с²/4, лемниската состоит из двух овалов, каждый из которых содержит точки F₁ и F₂, соответственно (рис.22).

Рис. 22

Задавая различные условия для р и с²/4 можно получать лемнискаты различного вида (рис. 23).

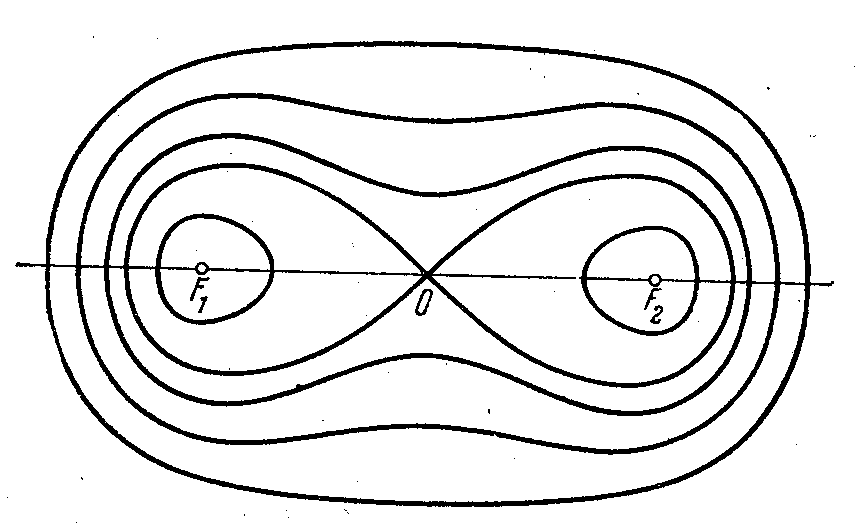
Рис. 23

Рассмотрим теперь на плоскости любое количество точек. F₁,F₂, ..., F_n. Точка М будет двигаться так, чтобы для нее оставалось неизменным произведение расстояний до каждой из взятых точек. Таким образом, получим кривую, форма которой зависти от того, как расположены точки F₁,F₂, ..., F_n друг относительно друга и какова величина неизменного произведения. Кривая эта называется лемнискатой с n фокусами.

Лемнискаты с двумя фокусами были рассмотрены нами выше. Беря разное число фокусов, располагая их по-разному и назначая ту или иную величину для произведения расстояний, получим лемнискаты самых удивительных очертаний. Начертить карандашом из некоторой точки А, не отрываясь от бумаги, так, чтобы изображение в конце вернулось в исходную точку А. Тогда оно опишет некоторую кривую; мы потребуем только, чтобы эта кривая нигде не пересекаласамое себя.

Рис. 24

Таким путем могут получиться разнообразные кривые, имеющие, например, очертания человеческой головы или птицы (рис. 24).

Имея такую произвольную кривую, можно так подобрать число п и расположение фокусов

F₁,F₂, ..., F_n

и назначить такую величину для неизменного произведения расстояний

МF₁ МF₂… МF_n = p

что соответствующая лемниската на глаз не будет отличаться от этой кривой. То есть возможные отклонения точки М, описывающей лемнискату, от нарисованной кривой - не будут превосходить ширину карандашного штриха (карандаш можно заранее отточить как угодно хорошо так, что штрих будет очень узким). Этот замечательный факт, говорящий о необычайном разнообразии н богатстве форм лемнискат с многими фокусами, доказывается совершенно строго, нo очень сложно, при помощи высшей математики.

Список литературы

1. Маркушевич А.И., Замечательные кривые, М., 1978 г., 48 стр. с илл.