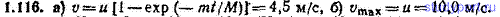1. 99. Система состоит из частицы 1 массы 0,100 г, частицы 2 массы 0,200 г и частицы 3 массы 0,300 г. Частица 1 помещается в точке с координатами (1,00; 2,00; 3,00), частица 2 — в точке с координатами (2,00; 3,00; 1,00), частица 3 — в точке с координатами (3,00; 1,00; 2,00) (значения координат даны в метрах). Найти радиус-вектор rC центра масс системы и его модуль.
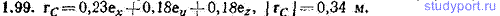
1.100. Из астрономических наблюдений установлено, что называемый барицентром центр масс системы Земля — Луна расположен внутри земного шара на расстоянии ηRЗ от центра Земли (η=0,730, RЗ — радиус Земли). Считая известными массу Земли mЗ, радиус Земли RЗ и средний радиус лунной орбиты R, вычислить массу Луны mЛ. Сравнить полученное значение с табличным.
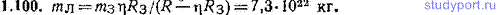
1.101. Однородный круглый конус имеет высоту h. На каком расстоянии l от вершины находится его центр масс?

1.102. Чему равен импульс p системы частиц в системе их центра масс?

1.103. Как ведет себя центр масс, если суммарный импульс системы частиц равен нулю?

1.104. Система взаимодействующих тел находится в поле сил тяжести вблизи поверхности Земли. Как ведет себя центр масс системы? Сопротивлением воздуха пренебречь.
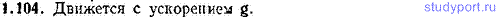
1.105. Тело массы m бросили под углом к горизонту с начальной скоростью v0. Спустя время τ тело упало на Землю. Пренебрегая сопротивлением воздуха, найти: а) приращение импульса тела Δp за время полета, б) среднее значение импульса <p> за время τ.
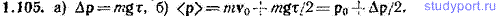
1.106. Частица массы m движется в плоскости x, y под действием постоянной по модулю силы F, поворачивающейся в этой плоскости по часовой стрелке с постоянной угловой скоростью ω. В начальный момент времени сила направлена по оси x, скорость частицы равна v0. Найти импульс частицы p в момент времени t.
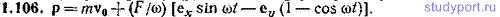
1.107. Два шара движутся навстречу друг другу вдоль прямой, проходящей через их центры. Масса и скорость первого шара равны 4,00 кг и 8,00 м/с, второго шара — 6,00 кг и 2,00 м/с. Как будут двигаться шары после абсолютно неупругого соударения?
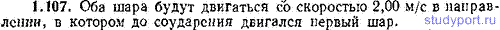
1.108. Два шара претерпевают центральный абсолютно неупругий удар. До удара шар массы m2 неподвижен, шар массы m1 движется с некоторой скоростью. Какая часть η первоначальной кинетической энергии теряется при ударе, если: а) m1=m2, б) m1=0,1*m2, в) m1=10*m2?
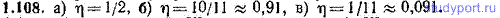
1.109. Шар массы m1 совершает центральный абсолютно упругий удар о покоящийся шар массы m2. а) При каком соотношении масс m1 и m2 первый шар полетит после удара в обратном направлении? б) Что происходит с первым шаром, если массы шаров одинаковы? в) Что происходит с первым шаром, если m1<<m2?

1.110. Два шара движутся навстречу друг другу вдоль оси x. Масса первого шара m1=0,200 кг, масса второго шара m2=0,300 кг. До столкновения проекции скоростей шаров на ось равны: v10=1 м/с, v20=-1 м/с. Найти проекции скоростей шаров v1x и v2x после их центрального абсолютно упругого соударения.
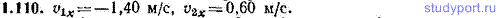
1.111. Шар массы m1, движущийся со скоростью v0, ударяет о неподвижный шар массы m2. После абсолютно упругого соударения шары летят со скоростями v1 и v2 в направлениях, указанных на рисунке. 1. При каком соотношении масс m1 и m2 возможны случаи: а) α=π/2, б) α=β≠0, в) α=β=0, г) α=π, β=0? 2. Возможен ли случай β=π/2? 3. Чему равно при α=π/2 предельное возможное значение угла β? Какую относительную долю η своей кинетической энергии передает первый шар второму в случаях: а) α=π/2, б) α=β≠0, в) α=β=0, г) α=π, β=0? 5. Сравнить результаты п. 4а – г. 6. Чему равно предельное значение η в случае 46? 7. При каких значениях m1, m2 и β первый шар после удара покоится? 8. Найти угол β в случае, если: а) α=π/2 и m1=0 99*m2, б) α=β≠0 и m1=m2. Сравнить угол разлета шаров (т. е. α+β) в случаях 8а и 86. 10. Доказать, что в случае m1=m2 при любом значении α (в пределах 0<α<π/2) угол разлета шаров равен π/2.
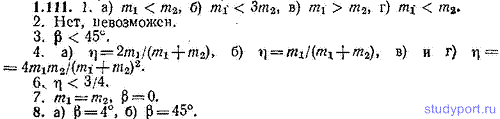
1.112. Два одинаковых шара претерпевают центральный удар. До удара второй шар неподвижен, первый движется со скоростью v0. Характер удара таков, что потеря энергии составляет η-ю часть той, которая имела бы место при абсолютно неупругом ударе. 1. Определить скорости шаров v1 и v2 после удара. Исследовать случаи: а) η=1, б) η=0.
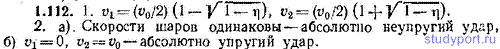
1.113. Вычислить скорости шаров из задачи 1.112 для значений η, равных: а) 0,1, б) 0,5, в) 0,9. Сравнить полученные результаты.
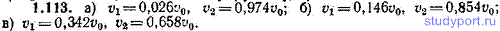
1.114. Расшалившиеся дети бросили мяч вслед проехавшему мимо грузовому автомобилю. С какой скоростью v отскочит мяч от заднего борта грузовика, если скорость автомобиля u=7,0 м/с, скорость v0 мяча непосредственно перед ударом равна 15,0 м/с и направлена по нормали к поверхности борта. Удар считать абсолютно упругим.
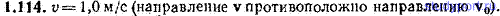
1.115. Протон начинает двигаться по направлению к свободной покоящейся альфа-частице «из бесконечности» (т. е. с расстояния, при котором взаимодействие между протоном и альфа-частицей пренебрежимо мало) со скоростью v0=1,00*106 м/с. Считая «соударение» центральным, определить, на какое минимальное расстояние rmin сблизятся частицы. При решении задачи учесть, что взаимная потенциальная энергия двух точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга, равна U=kq1q2/r (сравните с выражением U=-γm1m2/r для взаимной потенциальной энергии двух тяготеющих друг к другу точечных масс). В СИ числовое значение коэффициента пропорциональности k равно 9*109. Заряд протона равен +e, заряд альфа-частицы равен +2e, где e — элементарный заряд. Масса протона mp=l,67*10-27 кг, масса альфа-частицы mα=6,64*10-27 кг.
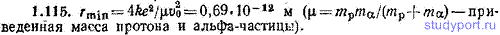
1.116. Водометный двигатель катера забирает воду из реки и выбрасывает ее со скоростью u=10,0 м/с относительно катера назад. Масса катера M=1000 кг. Масса ежесекундно выбрасываемой воды постоянна и равна m=10,0 кг/с. Пренебрегая сопротивлением движению катера, определить: а) скорость катера v спустя время t=1,00 мин после начала движения, б) какой предельной скорости vmax может достичь катер.