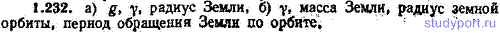1.213. В опыте, аналогичном тому, с помощью которого Кавендиш определил в 1798 г. гравитационную постоянную γ, массы малых и больших свинцовых шаров были равны соответственно m=0,729 кг и M=158 кг. Малые шары были укреплены на легком, подвешенном на стальной проволоке коромысле, длина которого, измеренная между центрами шаров, l=216 см. Диаметр проволоки равнялся 0,6 мм, длина была около метра. При расстоянии между центрами малого и соответствующего большого шаров, равном 300 мм, проволока, несущая коромысло с малыми шарами, закручивалась на угол α = 39,6”. Определенный экспериментально коэффициент пропорциональности k между углом закручивания проволоки и приложенным вращающим моментом равен 1,04*103 рад/(Н*м). Найти значение γ.
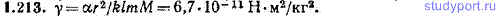
1.214. С какой силой F притягивают друг друга два одинаковых однородных шара массы m=1,000 кг каждый, если их центры отстоят друг от друга на расстояние r=1,00 м?

1.215. Два одинаковых однородных шара, соприкасаясь, притягивают друг друга с силой F. Как изменится сила, если увеличить массу шаров в n раз? Материал, из которого изготовлены шары, предполагается одним и тем же.
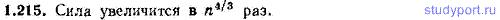
1.216. Имеется очень тонкий однородный прямой стержень длины l и массы M. На прямой, перпендикулярной к оси стержня и проходящей через его центр, находится на расстоянии b частица массы m. а) Найти модуль F силы, с которой стержень действует на частицу, если b=l=2a. б) Исследовать случай b>>l. в) Сравнить F с силой F', с которой взаимодействовали бы материальные точки массами M и m, находящиеся на расстоянии b=2a друг от друга.

1.217. Решить задачу 1.216, считая, что частица находится на оси стержня, на расстоянии b=l=2a от его центра.
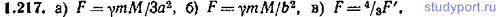
1.218. Имеется очень тонкое однородное кольцо массы M и радиуса R. На прямой, перпендикулярной к плоскости кольца и проходящей через его центр, находится на расстоянии x от центра частица массы m. Найти: а) взаимную потенциальную энергию U(x) частицы и кольца, б) силу Fx, действующую на частицу со стороны кольца. Силу вычислить двумя способами: 1) путем суммирования элементарных сил, 2) использовав выражение для U(x). в) Исследовать случай x>>R.
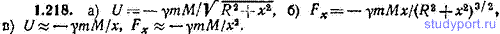
1.219. Имеется очень тонкий однородный диск радиуса R. Поверхностная плотность (масса единицы площади) диска равна σ. На прямой, перпендикулярной к плоскости диска и проходящей через его центр, находится на расстоянии b от диска частица массы m. Определить: а) силу F, с которой диск действует на частицу, б) при каком условии сила F отличается от своего предельного значения F∞, получающегося при R→∞, не более чем на 1%.
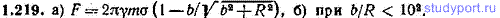
1.220. Имеется бесконечная очень тонкая однородная пластинка с поверхностной плотностью σ. На расстоянии b от нее находится частица массы m. а) Найти модуль F силы, с которой пластинка действует на частицу. б) Чем примечательно выражение для F? в) Как изменится результат, если пластинку с пренебрежимо малой толщиной заменить пластиной конечной толщины d, изготовленной из вещества с объемной плотностью ρ?
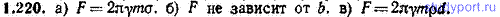
1.221. Имеется бесконечная однородная пластина толщины d=0,100 м, плотность которой ρ=10,0 г/см3. С какой силой F действует эта пластина на находящееся вблизи от нее тело массы m=1,00 кг?

1.222. С какой силой F (в расчете на единицу площади) притягивают друг друга две параллельные бесконечные однородные пластины плотности ρ=10,0 г/см3 и толщины d=0,100 м каждая?

1.223. Имеется бесконечный очень тонкий однородный прямой стержень с линейной плотностью (массой, приходящейся на единицу длины), равной λ. На расстоянии b от его оси находится частица массы m. а) Найти модуль F силы, с которой стержень действует на частицу. б) Частица какой массы M, находясь от частицы массы m на расстоянии b, действовала бы на нее с такой же силой?
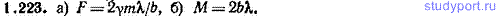
1.224. Как связаны телесный угол dΩ и поверхность dS, вырезаемая им на сфере радиуса R, центр которой совпадает с вершиной телесного угла?

1.225. Выразить в сферических координатах элемент поверхности dS сферы радиуса R, центр которой находится в начале координат.

1.226. Выразить в сферических координатах элементарный телесный угол dΩ, вершина которого помещается в начале координат.

1.227. Определить гравитационную силу F, которую будет испытывать материальная точка, находящаяся внутри однородного шарового слоя.

1.228. Внутри однородного шарового слоя находится однородный шаровой слой меньшего размера. Центры слоев не совпадают. Чему равна сила F взаимодействия между слоями?

1.229. Имеется очень тонкий однородный слой в виде полусферы радиуса R и массы М. В центре полусферы находится частица массы m. Найти модуль F силы, с которой слой действует на частицу.

1.230. Найти взаимную потенциальную энергию U(r) очень тонкого однородного шарового слоя и частицы массы m, находящейся на расстоянии г от центра слоя. Масса слоя равна М, радиус R. Рассмотреть случаи: a) r<R, б) r>R.

1.231. Воспользовавшись результатом предыдущей задачи, найти взаимную потенциальную энергию U(r) толстого шарового слоя и частицы массы m, находящейся на расстоянии r от центра слоя. Масса слоя равна М, внутренний радиус R1, внешний радиус R2. 1. Рассмотреть случаи: а) r<R1, б) r>R2. 2. Какое заключение о силе F, действующей на частицу со стороны слоя, можно сделать на основании ответа на п. 1а?

1.232. С помощью каких данных можно определить массу: а) Земли, б) Солнца?