64. Снаряд массой m = 5 кг, вылетевший из орудия, верхней точке траектории имеет скорость v = 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой m1 полетел в обратном направлении со скоростью v1 = 100 м/с. Определить скорость v2 второго меньшего осколка.

65. Лодка массой M = 150 кг и длиной l = 2,8 м стоит неподвижно в стоячей воде. Рыбак массой m = 90 кг в лодке переходит с носа на корму. Пренебрегая сопротивлением воды, определите, на какое расстояние s при этом сдвинется лодка.
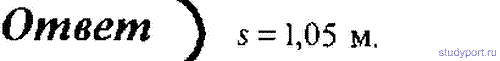
66. Снаряд, вылетевший из орудия со скоростью v0 , разрывается на два одинаковых осколка в верхней точке траектории на расстоянии l (по горизонтали). Один из осколков полетел в обратном направлении со скоростью движения снаряда до разрыва. Пренебрегая сопротивлением воздуха, определите, на каком расстоянии (по горизонтали) от орудия упадет второй осколок.
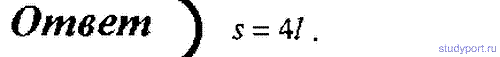
67. Платформа с песком общей массой M = 2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m = 8 кг и застревает в нем. Пренебрегая трением, определите, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда v = 450 м/с, а ее направление — сверху вниз под углом α = 30° к горизонту.
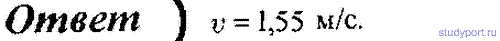
68. На железнодорожной платформе, движущейся по инерции со скоростью v0 = 3 км/ч, укреплено орудие. Масса платформы с орудием M = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m = 10 кг вылетает из ствола под углом α = 60° к горизонту. Определить скорость v снаряда (относительно Земли), если после вылета скорость платформы уменьшилась в n = 2 раза.

69. Две легкие тележки (массы соответственно m1 и m2 = 2m1) соединены между собой сжатой, связанной нитью пружиной. Пережигая нить, пружина распрямляется, и тележка разъезжается в разные стороны. Считая коэффициент трения для обеих тележек одинаковый, определить: 1) v1/v2 – отношение скоростей движения тележек; 2) t1/t2 – отношение времени, в течении которого тележки движутся; 3) s1/s2 – отношение путей пройденных тележкой.

70. Две одинаковые тележки массой М каждая движутся по инерции (без трения) друг за другом с одинаковой скоростью v0. В какой-то момент времени человек массой m, находящийся на задней тележке, прыгнул на переднюю тележку со скоростью u относительно своей тележки. Определите скорость v1 передней тележки.
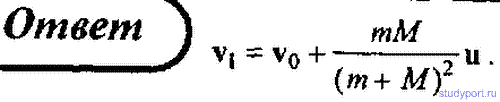
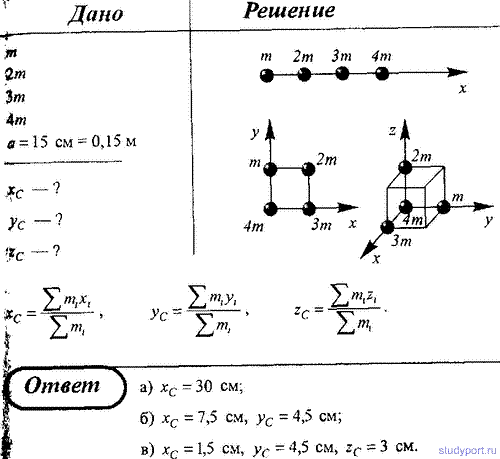
71. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m, Зm и 4m, в следующих случаях: а) шары расположены на одной прямой; б) шары расположены по вершинам квадрата; в) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. Направление координатных осей показано на рисунке.
72. Определите положение центра масс половины круглого диска радиусом R, считая его однородным.
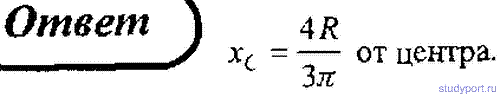
73. Определите координаты центра масс системы, состоящей из четырех шаров массами 2m, Зm, 4m и т, которые расположены в вершинах и в центре равностороннего треугольника со стороной a = 20 см. Направление координатных осей показано на рисунке.
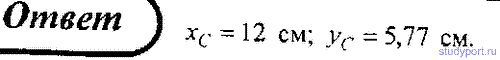
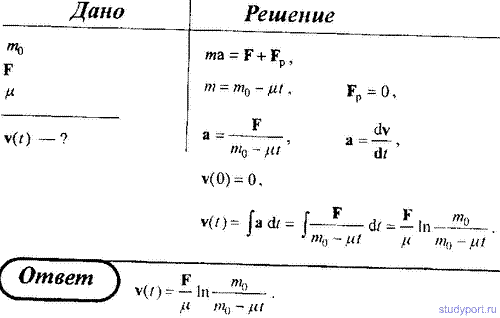
74. нагруженная песком железнодорожная платформа с начальной массой m0 начинает движение из состояния покоя под действием постоянной силы тяги F. Через отверстие в дне платформы высыпается песок с постоянной скоростью μ (кг/с) Определить v(t), т.е. зависимость скорости платформы от времени.
75. На катере массой m = 4,5 т находится водомет, выбрасывающий со скоростью u = 6 м/с относительно катера назад μ = 25 кг/с воды. Пренебрегая сопротивлением движению катера, определите: 1) скорость катера через t = 3 мин после начала движения; 2) предельно возможную скорость катера.
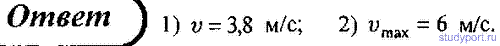
76. Ракета, масса которой в начальный момент времени М = 2 кг, запущена вертикально вверх. Относительная скорость выхода продуктов сгорания u = 150 м/с, расход горючего μ = 0,2 кг/с. Пренебрегая сопротивлением воздуха, определить ускорение a ракеты через t = 3 с после начала её движения. Поле силы тяжести считать однородным.

77. Ракета, масса М которой в начальный момент времени равна 300 г, начинает выбрасывать продукты сгорания с относительной скоростью u = 200 м/с. Расход горючего μ = 100 г/с. Пренебрегая сопротивлением воздуха и внешним силовым полем, определить: 1) за какой промежуток времени скорость ракеты станет равной v1 = 50 м/с; 2) скорость v2, которой достигнет ракета, если масса заряда m0 = 0,2 кг.

78. Ракета с начальной массой m0, начиная движение из состояния покоя, к некоторому моменту времени t израсходовав топливо массой m, развивает скорость v. Пренебрегая сопротивлением воздуха и внешним силовым полем, определите зависимость v от m, если скорость истечения топлива относительно ракеты равна u.

79. Ракета поднимается с нулевой начальной скоростью вертикально вверх. Начальная масса ракеты m0, скорость истечения газа относительно ракеты постоянна и равна u. Пренебрегая сопротивлением воздуха, выразите скорость ракеты v в зависимости от m и t (m — масса ракеты; t — время ее подъема). Поле силы тяжести считайте однородным.
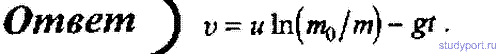
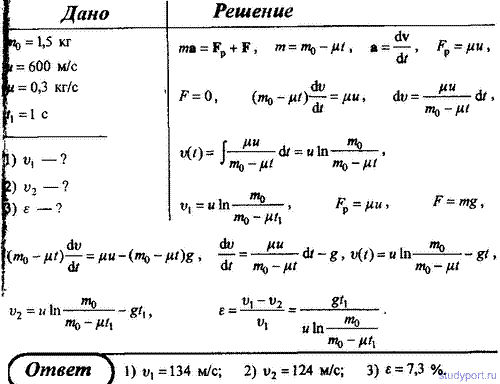
80. Ракета с начальной массой m0 = 1,5 кг, начинает движение из состояния покоя вертикально вверх, выбрасывая непрерывную струю газов с постоянной скоростью относительно нее скорости u = 600 м/с. Расход газа μ = 0,3 кг/c. Определить, какую скорость приобретет ракета через 1 секунду после начала движения, если она движется: 1) при отсутствии внешних сил; 2) в однородном поле силы тяжести. Оценить относительную погрешность, сделанную для данных условий задачи при пренебрежении внешним силовым полем.
/i

