140. Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению φ = A + B*t2 + C*t3 (B = 2 рад/с2, C = – 0,5 рад/с3). Определить момент сил M для t = 3 с.
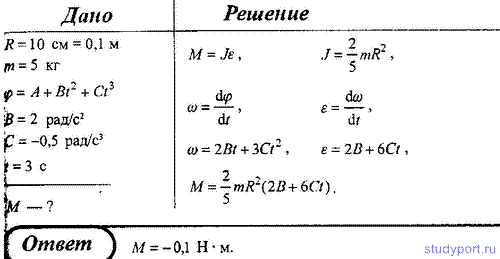
141. Вентилятор вращается с частотой n = 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав N = 50 оборотов, остановился. Работа A сил торможения равна 31,4 Дж. Определить: 1) момент сил М торможения; 2) момент инерции J вентилятора.

142. Маховик в виде сплошного диска, момент инерции которого J = 150 кг*м2, вращается с частотой n = 240 об/мин. Через t = 1 мин после начала действия сил торможения он остановился. Определите: 1) момент M сил торможения; 2) число оборотов маховика от начала торможения до полной остановки.
143. Сплошной однородный диск скатывается без скольжения с наклонной плоскости, образующей угол α с горизонтом. Определить линейное ускорение α центра диска.
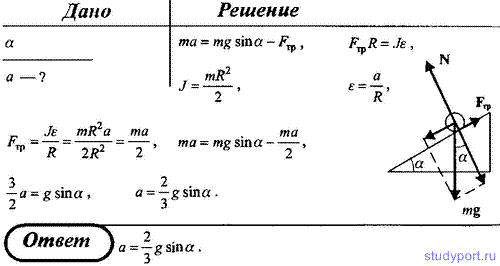
144. К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F = 100 Н. При вращении диска на него действует сила трения Mтр = 2 Н*м. Определить массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с2.

145. Частота вращения n0 маховика, момента инерции J которого равен 120 кг*м2, составляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время t = π мин. Считая трение в подшипниках постоянным, определите момент М сил трения.

146. Маховик в виде сплошного диска, момент инерции которого J = 1,5 кг*м2, вращаясь при торможении равнозамедленно, за время t = 1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Определить: 1) угловое ускорение ε маховика; 2) момент М сил торможения; 3) работу торможения А.

147. Колесо радиусом R = 30 см и массой m = 3 кг скатывается без трения по наклонной плоскости длиной l = 5 м и углом наклона α = 25° . Определить момент инерции колеса, если его скорость v в конце движения составляла 4,6 м/с.
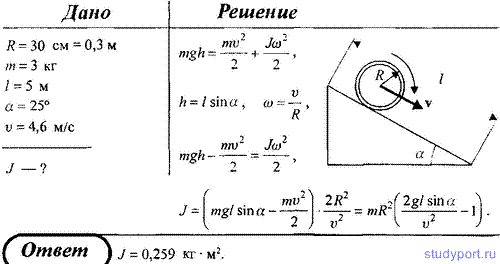
148. С наклонной плоскости, составляющей угол α = 30 градусов с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.
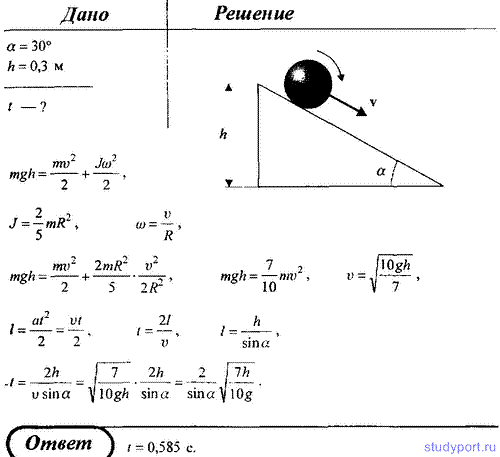
149. Полый тонкостенный цилиндр катится вдоль горизонтального участка дороги со скоростью v = 1,5 м/с. Определите путь, который он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути.

150. На однородный сплошной цилиндрический вал радиусом R = 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением а = 2 м/с2. Определить: 1) момент инерции J; 2) масса m1 вала.
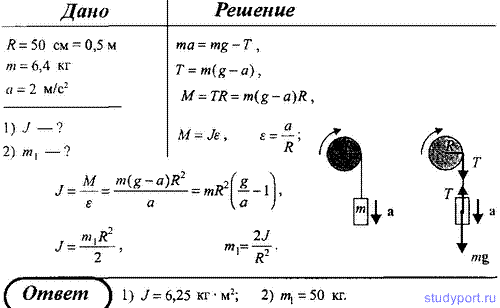
151. На однородный сплошной цилиндрический вал радиусом R=5 см и массой M = 10 кг намотана легкая нить, к концу которой прикреплен груз массой m = 1 кг. Определите: 1) зависимость s(t), согласно которой движется груз; 2) силу натяжения нити Т; 3) зависимость φ(t), согласно которой вращается вал; 4) угловую скорость φ вала через t = 1 с после начала движения; 5) тангенциальное (аτ) и нормальное (аn) ускорения точек, находящихся на поверхности вала.
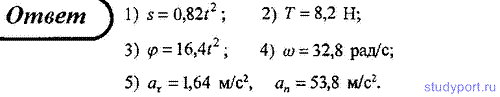
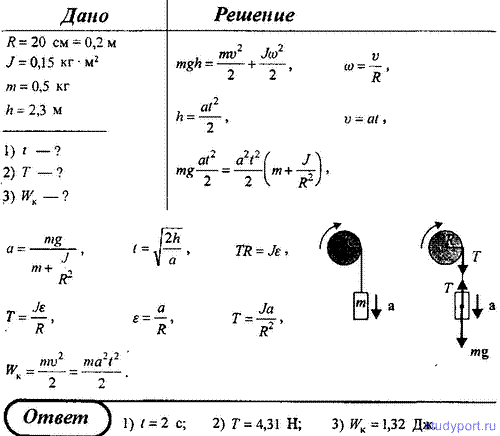
152. На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого J = 0,15 кг*м2, намотана легкая нить, к концу которой прикреплен груз массой m = 0,5 кг. До начала вращения барабана высота h груза над полом составляла 2,3 м. Определите: 1) зависимость s(t), согласно которой движется груз; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол.
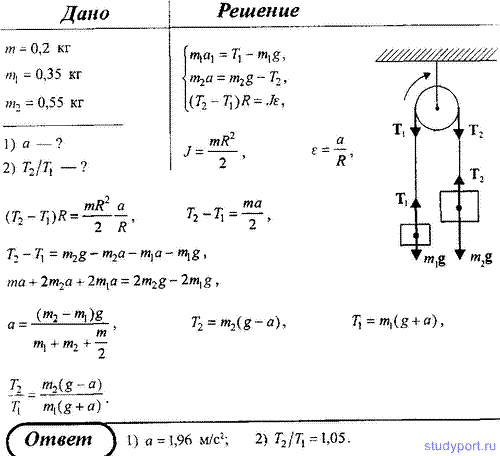
153. Через неподвижный блок в виде однородного цилиндра массой m = 0,2 кг перекинута невесомая нить, к концам которой прекреплены тела массами m1 = 0,35 кг и m2 = 0,55 кг. Пренебрегая трением в оси блока, определить: 1) ускорение; 2) отношение Т2/Т1 сил натяжения нити.
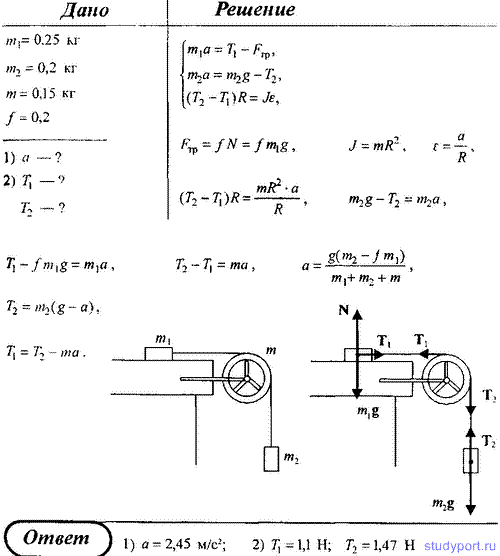
154. Тело массой m1 = 0,25 кг, соединенное невесомой нитью посредством блока (в виде полого тонкостенного цилиндра) с телом массой m2 = 0,2 кг, скользит по поверхности горизонтального стола. Масса блока m = 0,15 кг. Коэффициент трения f тела о поверхность равен 0,2. Пренебрегая трением в подшипниках, определите: 1) ускорение а, с которым будет двигаться эти тела; 2) силы натяжения T1 и T2 нити по обе стороны блока.
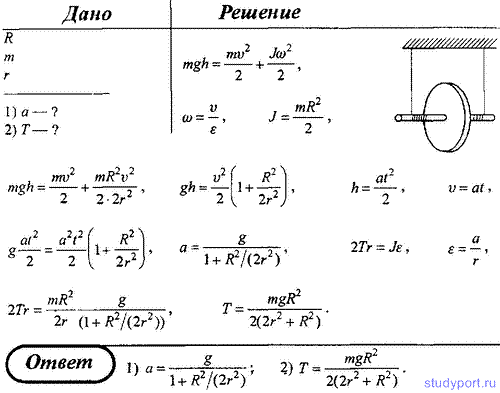
155. Для демонстрации законов сохранения применяется маятник Максвелла, представляющий собой массивный диск радиусом R и массой m, туго насаженный на ось радиусом r, которая подвешивается на двух предварительно намотанных на нее нитях. Когда маятник отпускают, то он совершает возвратно-поступательное движение в вертикальной плоскости при одновременном движении диска вокруг оси. Не учитывая силы сопротивления и момент инерции оси, определить: 1) ускорение поступательного движения маятника; 2) силу натяжения нити.
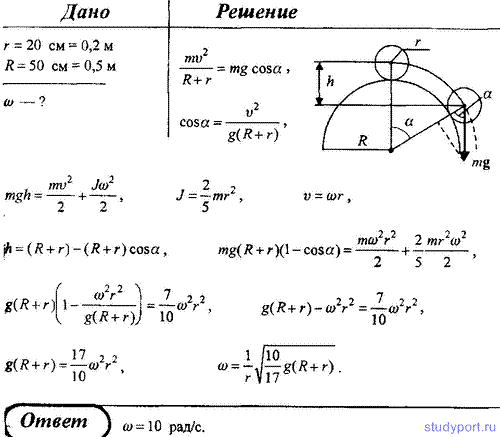
156. Однородный шар радиусом r = 20 см скатывается без скольжения с вершины сферы радиусом R = 50 см. Определить угловую скорость w шара после отрыва от поверхности сферы.
157. Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε = 0,4 рад/с2. Определите кинетическую энергию маховика через время t2 = 25 с после начала движения, если через t = 10 с после начала движения момент импульса L1 маховика составлял 50 кг * м2/с.
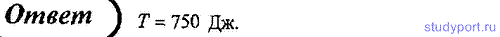
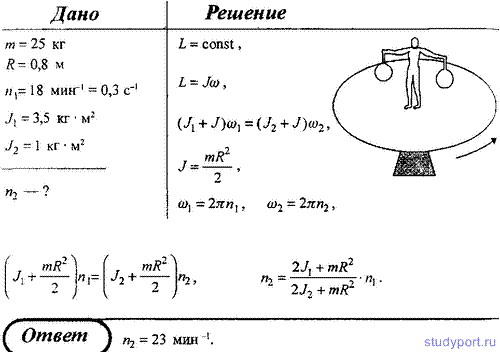
158. Горизонтальная платформа массой m = 25 кг и радиусом R = 0,8 м вращается с частотой n1 = 18 мин-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J1 = 3,5 кг*м2 до J2 = 1 кг*м2.
159. Человек, стоящий на скамье Жуковского, держит в руках стержень длиной l = 2,5 м и массой m = 8 кг, расположенный вертикально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции J = 10 кг * м2 и вращается с частотой n1 = 12 мин-1. Определите частоту n2 вращения системы, если стержень повернуть в горизонтальное положение.