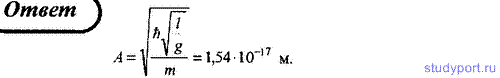108. Электрон с энергией E = 5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите коэффициент D прозрачности потенциального барьера.

109. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определите в электрон-вольтах разность энергий U - E, при которой вероятность прохождения электрона сквозь барьер составит 0,5.
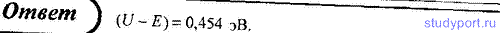
110. Протон с энергией E = 5 эВ движется в положительном направлении оси x, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определите вероятность прохождения протоном этого барьера. Во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях.

111. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси x электрона U - E = 5 эВ. Определите, во сколько раз изменится коэффициент прозрачности D потенциального барьера для электрона, если разность U - E возрастает в 4 раза.

112. Частица с энергией E движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E > U. Запишите уравнение Шредингера для областей 1 и 2.
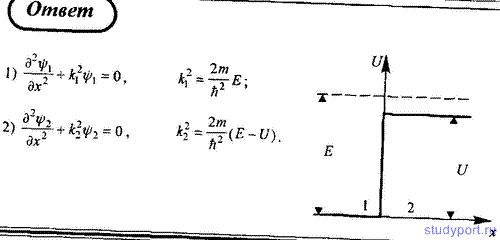
113. Для условия задачи 112 запишите решение уравнений Шредингера для областей 1 и 2. ψ -функция обычно нормируется так, что A1 = 1. Представьте графически качественный вид ψ -функций.
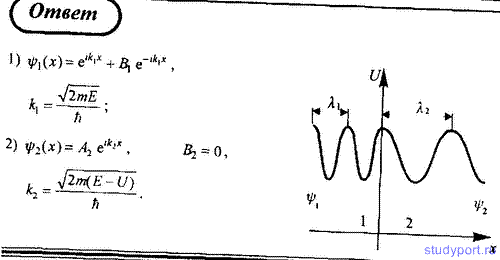
114. Частица с энергией E = 10 эВ движется в положительном направлении оси x, встречая на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 5 эВ. Определите коэффициент преломления n волн де Бройля на границе потенциального барьера.

115. Электрон с длиной волны де Бройля λ1 = 100 пм, двигаясь в положительном направлении оси x, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите длину волны де Бройля после прохождения барьера.
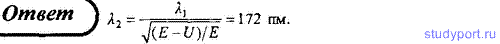
116. Частица с энергией E = 50 эВ, двигаясь в положительном направлении оси x, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 20 эВ. Определите вероятность отражения частицы от этого барьера.

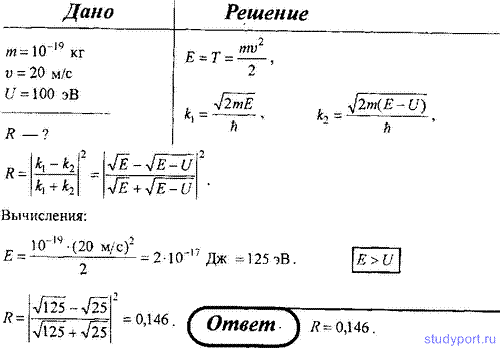
117. Частица массой m = 10-19 кг, двигаясь в положительном направлении оси x со скоростью v = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определите коэффициент отражения R волн де Бройля на границе потенциального барьера.
118. Частица с энергией Е движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E < U. Запишите уравнение Шредингера для областей 1 и 2.
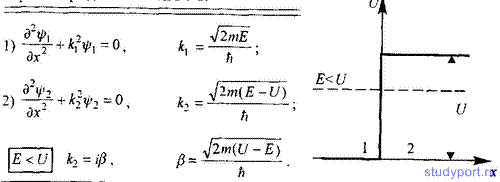
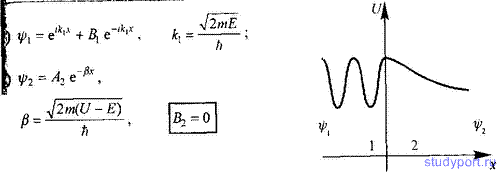
119. Для условия задачи 118 запишите решение уравнений Шредингера для областей 1 и 2. ψ - функция обычно нормируется так, что A1 = 1. Представьте графически качественный вид ψ -функций.
120. Электрон с длиной волны λ де Бройля, равной 120 им, движется в положительном направлении оси х и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 200 эВ. Определите коэффициент отражения R волн де Бройля на границе потенциального барьера.

121. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный барьер высотой U, причем E < U. Принимая A1 = 1 (как это обычно делается) и используя условия непрерывности волновой функции и ее первой производной на границе областей 1 и 2, определите плотность вероятности |ψ2(0)|2 обнаружения частицы в точке x = 0 области 2.

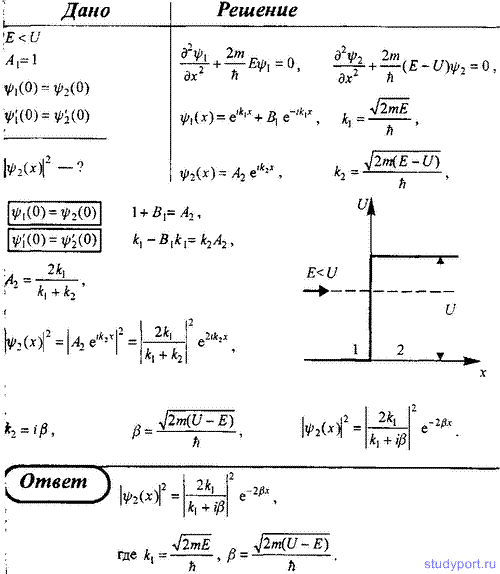
122. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U, причем E < U. Принимая A1 = 1 (как это обычно делается) и используя условия непрерывности волновой функции и ее первой производной на границе областей 1 и 2, определите плотность вероятности обнаружения частицы на расстоянии x от потенциального барьера.
123. Докажите, что волновая функция ψ(x) = Ax*e –корень(mk)/2h*x^2 может быть решением уравнения Шредингера для гармонического осциллятора, масса которого m и постоянная квазиупругой силы k. Определите собственное значение полной энергии осциллятора.

124. Частица массой m движется в одномерном потенциальном поле U(x) = kx2/2 (гармонический осциллятор). Волновая функция, описывающая поведение частицы в основном состоянии, имеет вид ψ(x) = Ae-ax^2 , где A — нормировочный коэффициент; a—положительная постоянная. Используя уравнение Шредингера, определите: 1) постоянную a; 2) энергию частицы в этом состоянии.
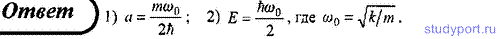
126. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли.

127. Рассматривая математический маятник массой m = 100 г и длиной l = 0,5 м в виде гармонического осциллятора, определите классическую амплитуду A маятника, соответствующую энергии нулевых колебаний этого маятника.