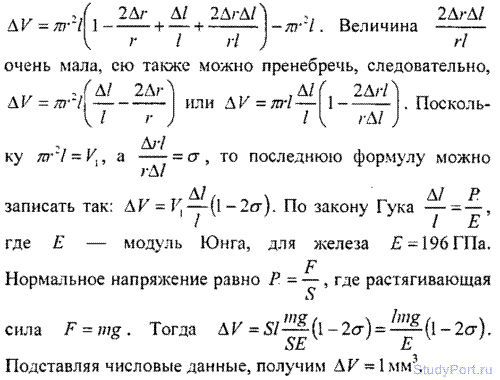8.21. При растяжении медной проволоки, поперечное сечение которой S = 1,5 мм2, начало остаточной деформации наблюдалось при нагрузке F = 44,1 Н. Каков предел упругости p материала проволоки?

8.22. Каким должен быть предельный диаметр d стального троса, чтобы он выдержал нагрузку F = 9,8 кН?
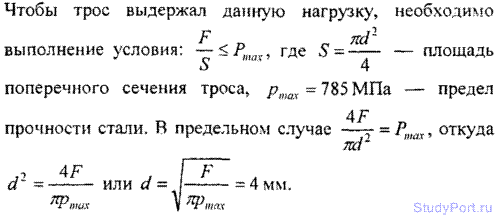
8.23. Найти длину l медной проволоки, которая, будучи подвешена вертикально, начинает рваться под действием собственной силы тяжести.

8.24. Решить предыдущую задачу для свинцовой проволоки.
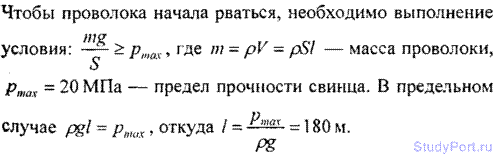
8.25. Для измерения глубины моря с парохода спустили гирю на стальном тросе. Какую наибольшую глубину l можно изме-
рить таким способом? Плотность морской воды p = 103 кг/м3. Массой гири по сравнению с массой троса пренебречь.
8.26. С крыши дома свешивается стальная проволока длиной l = 40м и диаметром d = 2 мм. Какую нагрузку F может выдержать эта проволока? На сколько удлинится эта проволока, если на ней повиснет человек массой m = 70 кг? Будет ли наблюдаться остаточная деформация, когда человек отпустит проволоку? Предел упругости стали p = 294 МПа.
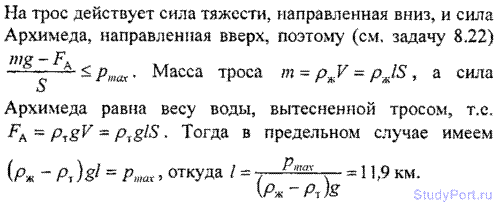


8.27. К стальной проволоке радиусом r = 1 мм подвешен груз массой m = 100 кг. На какой наибольший угол а можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении этим грузом положения равновесия?

8.28. К железной проволоке длиной l = 50 см и диаметром d = 1мм привязана гиря массой m = 1кг. С какой частотой n можно равномерно вращать в вертикальной плоскости такую проволоку с грузом, чтобы она не разорвалась?

8.29. Однородный медный стержень длиной l = 1м равномерно вращается вокруг вертикальной оси, проходящей через один из его концов. При какой частоте вращения стержень разорвется?

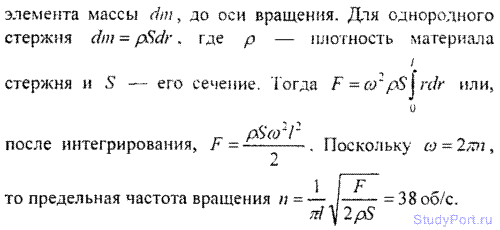
8.30. Однородный стержень равномерно вращается вокруг вертикальной оси, проходящей через его середину. Стержень разрывается, когда скорость конца стержня достигает v = 380 м/с. Найти предел прочности p материала стержня.
Плотность материала стержня p = 7,9 • 10' кг/г3.

8.31. К стальной проволоке длиной / = 1м и радиусом r = 1 мм подвесили груз массой m = 100 кг. Найти работу А растяжения проволоки.
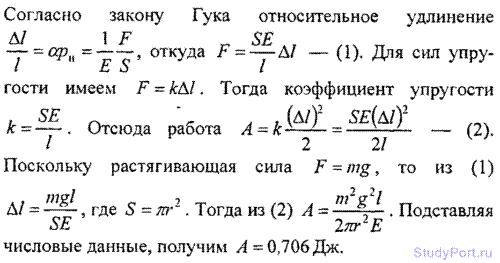
8.32. Из резинового шнура длиной l = 42 см и радиусом r = 3 мм сделана рогатка. Мальчик, стреляя из рогатки, растянул резиновый шнур на dl = 20 см. Найти модуль Юнга для этой резины, если известно, что камень массой m = 0,02 кг, пущенный из рогатки, полетел со скоростью v = 20 м/с. Изменением сечения шнура при растяжении пренебречь.


8.33. Имеется резиновый шланг длиной l = 50 см и внутренним диаметром d1 = 1 см. Шланг натянули так, что его длина стала на dl = 10 см больше. Найти внутренний диаметр d2 натянутого шланга, если коэффициент Пуассона для резины ? = 0,5 .

8.34. На рис. АВ — железная проволока, CD — медная проволока такой же длины и с таким же поперечным сечением, BD— стержень длиной l = 80 см. На стержень подвесили груз массой m = 2 кг. На каком расстоянии х от точки В надо его подвесить, чтобы стержень остался горизонтальным?

8.35. Найти момент пары сил M, необходимый для закручивания проволоки длиной l = 10 см и радиусом r = 0,1 мм на угол
? = 10. Модуль сдвига материала проволоки N = 4,9 • 1010 Па.
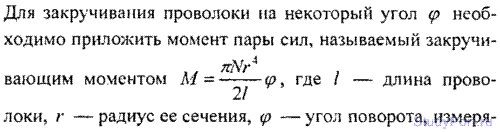
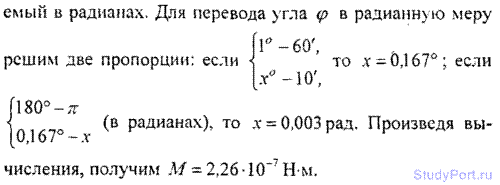
8.36. Зеркальце гальванометра подвешено на проволоке длиной l = 10см и диаметром d = 0,01мм. Найти закручивающий момент М, соответствующий отклонению зайчика на величину а = 1 мм по шкале, удаленной на расстояние L = 1 м от зеркальца.
Модуль сдвига материала проволоки N = 4 • 10ю Па.

8.37. Найти потенциальную энергию W проволоки длиной l = 5 см и диаметром d = 0,04 мм, закрученной на угол ? = 10.
Модуль сдвига материала проволоки N = 5,9 • 1010 Па.

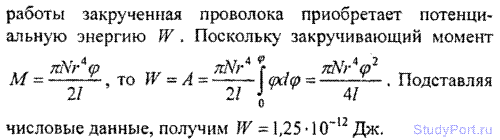
8.38. При протекании электрического тока через обмотку гальванометра на его рамку с укрепленным на ней зеркальцем
действует закручивающий момент M = 2*10-13Н*м. Рамка при этом поворачивается на малый угол ?. На это закручивание
идет работа А = 8,7 • 10-16 Дж. На какое расстояние а переместится зайчик от зеркальца по шкале, удаленной на расстояние L = 1 м от гальванометра?

8.39. Найти коэффициент Пуассона а, при котором объем проволоки при растяжении не меняется.
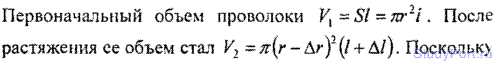
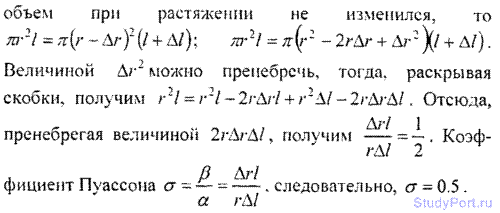
8.40. Найти относительное изменение плотности цилиндрического медного стержня при сжатии его давлением
pн=9.8*107 Па. Коэффициент Пуассона для меди ? = 0,34 .


8.41. Железная проволока длиной l = 5м висит вертикально. На сколько изменится объем проволоки, если к ней привязать гирю массой m = 10кг? Коэффициент Пуассона для железа ? = 0,3.