2.81. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули m1 = 5 г, масса шара т2 = 0.5 кг. Скорость пули v1 = 500 м/с. При каком предельном расстоянии l от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?
Решение:

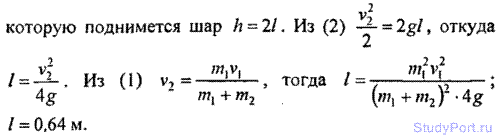
2.82. Деревянным молотком, масса которого т1 = 0,5 кг, ударяют о неподвижную стенку. Скорость молотка в момент удара v1 = 1 м/с. Считая коэффициент восстановления при ударе молотка о стенку k = 0,5, найти количество теплоты Q, выделившееся при ударе. (Коэффициентом восстановления материала тела называют отношение скорости после удара к его скорости до удара.)
Решение:
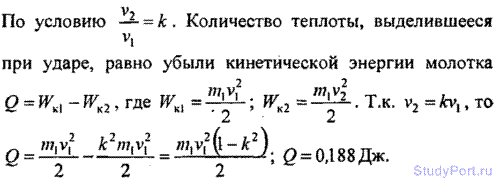
2.83. В условиях предыдущей задачи найти импульс силы Fdt, полученный стенкой за время удара.
Решение:

2.84. Деревянный шарик массой т = 0,1 кг падает с высоты h1 = 2 м. Коэффициент восстановления при ударе шарика о пол к = 0,5. Найти высоту h2 , на которую поднимется шарик после удара о пол, и количество теплоты Q, выделившееся при ударе.
Решение:

2.85. Пластмассовый шарик, падая с высоты h1 = 1 м несколь раз отскакивает от пола. Найти коэффициент восстановления к при ударе шарика о пол, если с момента падения до второго удара о пол прошло время t = 1,3 с.
Решение:
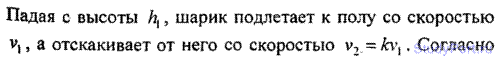

2.86. Стальной шарик, падая с высоты h1 = 1,5 м на стальную плиту, отскакивает от нее со скоростью v2 = 0,75 • v1, где v1— скорость, с которой он подлетает к плите. На какую высоту h2 он поднимется? Какое время t пройдет с момента падения до второго удара о плиту?
Решение:


2.87. Металлический шарик, падая с высоты h1 = 1 м на стальную плиту, отскакивает от нее на высоту h2 =81 см. Найти коэффициент восстановления к при ударе шарика о плиту.
Решение:

2.88. Стальной шарик массой m = 20 г, падая с высоты h1 = 1 м на стальную плиту, отскакивает от нес на высоту h2=81см. Найти импульс силы Fdt, полученный плитой за время удара, и количество теплоты Q, выделившееся при ударе.
Решение:
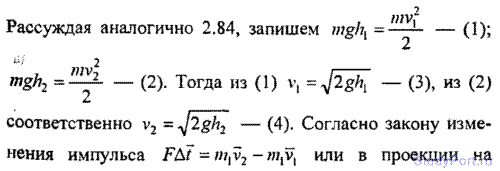

2.89. Движущееся тело массой m1, ударяется о неподвижное тело массой т2. Считая удар неупругим и центральным, найти, какая часть кинетической энергии WKl первого тела переходит при ударе в тепло. Задачу решить сначала в общем виде, а затем рассмотреть случаи: а) m1 = т2; б) m1 = 9т2.
Решение:

2.90. Движущееся тело массой m1 ударяется о неподвижное тело массой т2. Считая удар упругим и центральным, найти, какую часть кинетической энергии Wк] первое тело передает второму при ударе. Задачу решить сначала в общем виде, а затем рассмотреть случаи: а)m1 = m2; б)m1 = 9т2.
Решение:

2.91. Движущееся тело массой т{ ударяется о неподвижное тело массой т2. Каким должно быть отношение масс т{/т2, чтобы при центральном упругом ударе скорость первого тела уменьшилась в 1,5 раза? С какой кинетической энергией W'k2 начинает двигаться при этом второе тело, если первоначальная кинетическая энергия первого тела Жк1 = 1 кДж?
Решение:


2.92. Нейтрон (масса т0) ударяется о неподвижное ядро атома углерода (m = 12т0). Считая удар центральным и упругим, найти, во сколько раз уменьшится кинетическая энергия WK ней при ударе.
Решение:

2,93. Нейтрон (масса т0) ударяется о неподвижное ядро: а) атома углерода (m = 12т0); б) атома урана (m = 235m0). Считая удар центральным и упругим, найти, какую часть скорости v потеряет нейтрон при ударе.
Решение:

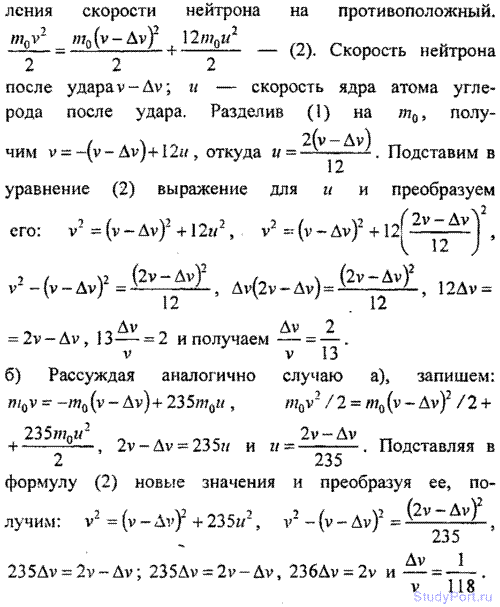
2.94. На какую часть уменьшится вес тела на экваторе вследствие вращения Земли вокруг оси?
Решение:
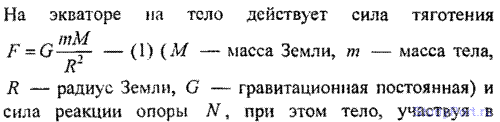

2.95. Какой продолжительности Т должны были бы быть сутки на Земле, чтобы тела на экваторе не имели веса.
Решение:
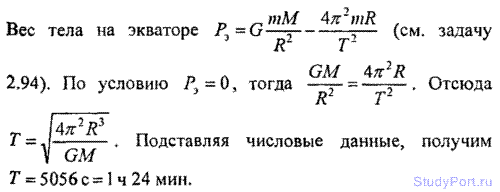
2.96. Трамвайный вагон массой m = 5 т идет по закруглению радиусом R = 128 м. Найти силу бокового давления F колес на рельсы при скорости движения v = 9 км/ч.
Решение:

2.97. Ведерко с водой, привязанное к веревке длиной l = 60 см, равномерно вращается в вертикальной плоскости. Найти наименьшую скорость v вращения ведерка, при которой в высшей точке вода из него не выливается. Какова сила натя веревки Т при этой скорости в высшей и низшей точках окружности? Масса ведерка с водой m = 2 кг.
Решение:

2.98. Камень, привязанный к веревке длиной l = 50 см, равно вращается в вертикальной плоскости. При какой частоте вращения п веревка разорвется, если известно, что она разрыва при десятикратной силе тяжести, действующей на камень?
Решение:
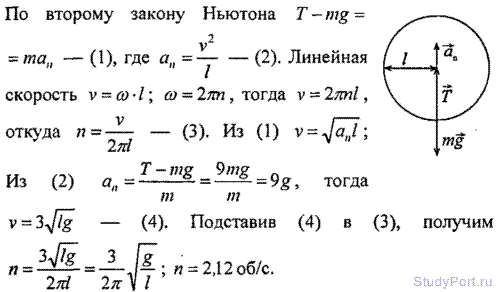
2.99. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу т камня, если известно, что разность между максимальной и минимальной силами натяжения веревки dT = 10 Н.
Решение:

2.100. Гирька, привязанная к нити длиной l = 30 см, описыва в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой п вращается гирька?
Решение:


