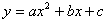Функция вида называется квадратичной функцией.



Квадратичную функцию можно представить в виде



Областью определения этой функции является множество всех действительных чисел.

Область значений лежит в промежутке 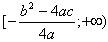, если a > 0, и в промежутке 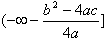, если a < 0.



Графиком квадратичной функции является парабола. Вершина параболы находится в точке

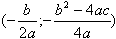
Парабола симметрична относительно прямой 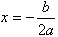. Ветви параболы направлены вверх, если a > 0.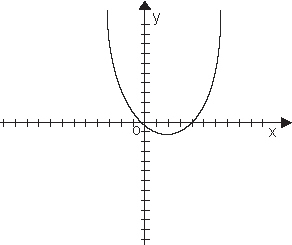



Ветви параболы направлены вниз, если a < 0.



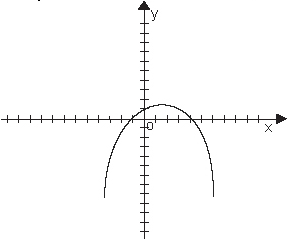
Парабола пересекает ось ОХ в точках x₁ и x₂ , где x₁ и x₂  - корни квадратного уравнения .

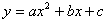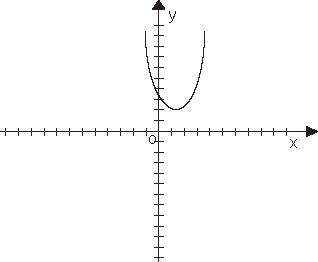
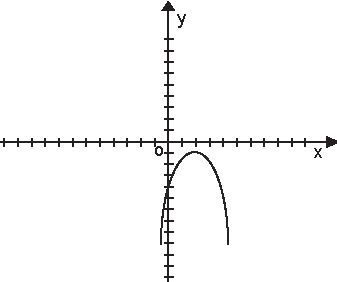
 Если квадратное уравнение не имеет корней (дискриминант отрицательный), то парабола лежит выше или ниже оси ОХ, (если a < 0, то ниже; если a > 0, то выше).



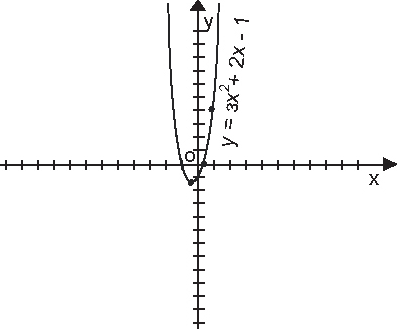
Пример: Построить график функции .

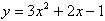Графиком функции является парабола. Ветви параболы направлены вверх. Вершина параболы находится в точке 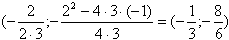. Осью симметрии параболы будет прямая 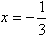. Парабола пересекает ось ОХ в точках .

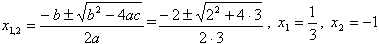Для точности построения, построим таблицу:



Строим график: