Для любых a и b верны равенства:



a³ - b³ = (a – b)(a² + ab + b²)  (разность кубов)

a³ + b³ = ( a + b)(a² - ab + b²)  (сумма кубов)

Докажем каждую из этих формул.

Формулы будем доказывать справа налево, то есть



(a – b)(a² + ab + b²)  = aa² + aab + ab² - ba² - bab -bb² = a³ + a²b + ab² - ba² - b²a - b³ = a³ - b³.



(a + b)(a² - ab + b²) = aa² - aab + ab² + ba² - bab + bb² = a³ - a²b + ab² - ba² - b²a + b³ = a³ + b^3.



Эти формулы часто используются при преобразовании и упрощение алгебраических выражений.

Приведем некоторые примеры.



Пример 1:

Сократите дробь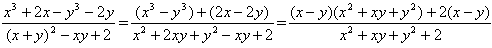 



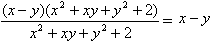
Пример 2:

Сократите дробь