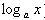), называют такое число m, что 
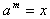. Очевидно, что для -x значение логарифма не определено.Примеры:
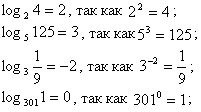
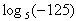не определен, так как нет такой степени числа 5, которая равна -125.Десятичным логарифмом числа x называется логарифм этого числа по основанию 10 (пишут
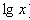). По-другому: = 
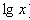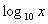.Примеры:
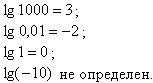
Натуральным логарифмом числа x, называется логарифм этого числа по основанию e (пишут
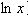). По-другому: =
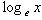. e (экспонента) – это иррациональное число, приблизительное значение которого e=2,718281828459045…. Значения натуральных логарифмов можно вычислить только приближенно. Однако, натуральные логарифмы широко используются при решении многих задач физики и прикладной математики.Свойства логарифма.
Логарифмы (в том числе натуральные и десятичные) обладают следующими свойствами:
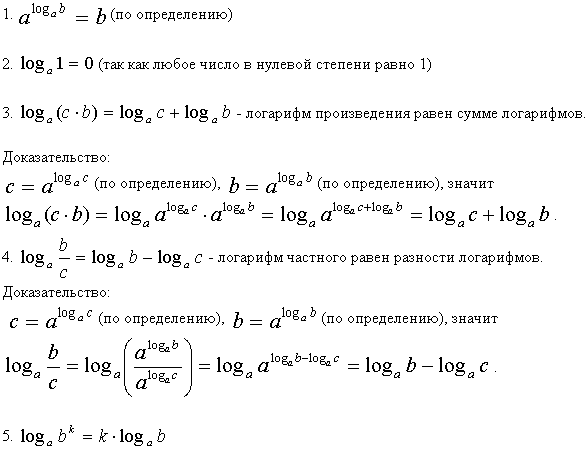
Доказательство:
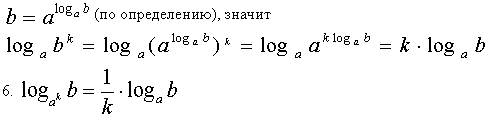
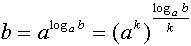(по определению), значит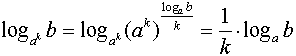
.Приведенные выше формулы используются при преобразовании выражений, решении уравнений и неравенств.
Пример:
Решить уравнение
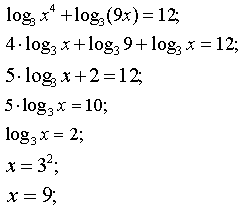
Ответ: x = 9.
