Неравенства вида (x-a₁)^k1 • (x-a₂)^k2 • ... • (x-a_n)^kn > 0, k₁, k₂, k_n ∈ N ( знак может быть не только “>”, но и “<”, и “⩽”, и “⩾”) решаются следующим способом :

1. Разбиваем числовую ось точками a₁, a₂ … a_n на промежутки. Если стоят знаки “⩽”, или “⩾” эти точки входят в интервал – на рисунке их закрашиваем.

2. На каждом из получившихся промежутков выражение (x-a₁)^k1 • (x-a₂)^k2 • ... • (x-a_n)^kn не меняет знак, поэтому определяем знак – “+” или “-“, определяя знак выражения в одной из точек каждого промежутка. На рисунке ставим над промежутком соответствующий знак

3. Если знак неравенства > или ⩾, то решением будет объединение тех промежутков, над которыми стоял знак “+”. Если знак неравенства < или ⩽, то решением будет объединение тех промежутков, над которыми стоял знак “-”.

Пример. Решить неравенство (x+3)(x-11)(x-5)²(x+6)³ ⩾ 0.

Разбиваем числовую прямую точками -3, 11, 5, -6 на промежутки (так как знак неравенства , эти точки закрашиваем).

Расставляем знаки:

Из промежутка (-∞; -6] возьмем точку -100, выражение (-100+3)(-100-11)(-100-5)²(-100+6)³ отрицательно, значит, ставим знак “-”.

Из промежутка [-6; -3] возьмем точку -5, выражение (-5+3)(-5-11)(-5-5)²(-5+6)³ положительно, значит ставим знак “+”.

Из промежутка [-3; 5] возьмем точку 0, выражение (0+3)(0-11)(0-5)²(0+6)³ отрицательно, значит, ставим знак “-”.

Из промежутка [5; 11] возьмем точку 10, выражение (10+3)(10-11)(10-5)²(10+6)³ отрицательно, значит, ставим знак “-”.

Из промежутка [11; +∞) возьмем точку 100, выражение (100+3)(100-11)(100-5)²(100+6)³ положительно, значит, ставим знак “+”.

Расставляем знаки.

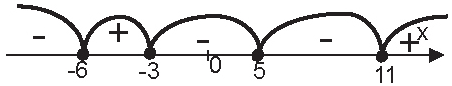
Итак, решением будет промежуток [-6; -3] ∪ [11; +∞) ∪ {5}. Про точку 5 нельзя забывать, так как она тоже обращает неравенство в истинное. Это очень распространенная ошибка.

Методом интервалов можно решать и неравенства вида

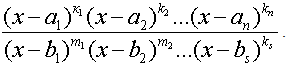
Здесь разбиваем числовую ось на промежутки точками a₁, a₂ … a_n и b₁, b₂ … b₅. Точки a₁, a₂ … a_n закрашиваем или не закрашиваем, в зависимости от того является неравенство строгим или нет. А точки b₁, b₂ … b₅ не закрашиваем никогда, так как в этих точках знаменатель обращается в ноль, а на ноль делить нельзя.

Пример:

Решить неравенство .

Разбиваем координатную ось на промежутки точками -4, 1, 10. Точки -4 и 1 закрашиваем, а точку 10 – нет.

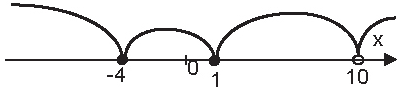
Расставляем знаки, как в предыдущем примере.

По рисунку видим, что решением будет промежуток [-4; 1] ∪ (10; +∞).

Ответ: x ∈ [-4; 1] ∪ (10; +∞).