Системой уравнений называется совокупность уравнений, для которых нужно найти значения неизвестных, удовлетворяющие одновременно всем уравнениям системы.
Значения неизвестных, удовлетворяющие одновременно всем уравнением системы называются решениями системы.
Примеры систем уравнений:
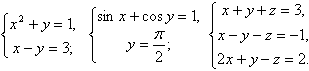
Системы уравнений могут состоять из двух и более уравнений и содержать одну и более переменных. Система уравнений может не иметь решений, иметь несколько решений, иметь бесконечное множество решений. Система уравнений, не имеющая решений, называется несовместной.
В школьной программе изучаются системы, содержащие две переменных.
Для решения различных видов систем разработано много различных методов решения, но в рамках школьного курса рассматриваются два основных метода.
Первый метод заключается в том, что мы в одном из уравнений выражаем одну переменную через другую. Полученное выражение, подставляем во второе уравнение вместо этой переменной и получаем уравнение с одной неизвестной. Это уравнение с одной неизвестной решаем известными нам способами.
Второй метод заключается в том, что мы умножаем одно из уравнений на подходящее число так, чтобы, сложив это уравнение с другим, исключить одну переменную и получить уравнение с одной неизвестной.
Примеры решения систем уравнений.
1. Решить систему уравнений ![]()
Решим эту систему обоими методами – ответ должен получиться одинаковый.
Первый метод.
Выразим во втором уравнении y через x:
![]()
Подставим это выражение в первое уравнение вместо y:
![]()
Решим верхнее уравнение с одной неизвестной:
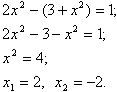
Мы нашли два возможных значения для первой переменной. Теперь найдем соответствующие значения для второй:
y1 = -(3x+x12) = -(3+22) = -7; y2 = -(3x+x22) = -(3+(-2)2) = -7
Ответ: {(2;-7), (-2;-7)}.
Второй метод.
Сложим первое уравнение со вторым – должен исключиться у:
![]()
Решением верхнего уравнения будет два значения х: x1 = 2; x2 = -2.
Мы нашли два возможных значения для первой переменной. Теперь найдем соответствующие значения для второй, решив второе уравнение, подставив в него вместо х его значения:
-22-y1 = 3, -y1 = 7, y1 = -7;
-(-2)2-y2 = 3, -y2 = 7, y2 = -7.
Ответ: {(2;-7), (-2;-7)}.

