Системой неравенств называется совокупность неравенств, для которых нужно найти значения неизвестных, удовлетворяющие одновременно всем неравенствам системы.

Значения неизвестных, удовлетворяющие одновременно всем уравнением системы называются решениями системы.

Примеры систем неравенств:

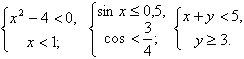
Системы неравенств могут состоять из двух и более неравенств и содержать одну и более переменных. Система неравенств может не иметь решений, иметь несколько решений, иметь бесконечное множество решений.

В школьной программе изучаются системы, содержащие одну переменную.

Для решения различных видов систем разработано много различных методов решения, но   в рамках школьного курса рассматривается один самый простой метод. Он заключается в том, что мы решаем каждое неравенство в отдельности, а затем все полученные решения пересекаем на координатной оси.    

Примеры решения систем неравенств.

1. Решить систему неравенств 

Решим первое неравенство:

x²-4 < 0;

(x-2)(x+2) < 0.

Решим это неравенство методом интервалов.

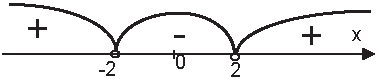
Решением этого неравенства будет промежуток (-2;2).

Второе неравенство уже решено - пересекаем решения первого и второго неравенства.

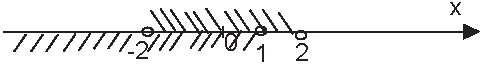
Итак, решением системы неравенств будет промежуток (-2;1).

Ответ: (-2;1).

 2. Решить систему неравенств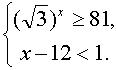 

Решим первое неравенство:

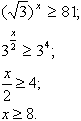
Решим второе неравенство:

x-12 < 1;

x < 13.

Пересекаем решения первого и второго неравенства.

Итак, решение системы неравенств - промежуток [8;13).

Ответ: [8;13).