Рассмотрим график некоторой функции y = f(x).

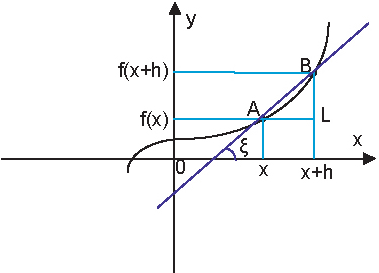
Отметим на нем некоторую точку А с координатами (x, f(x)) и недалеко от нее точку В с координатами (x+h, f(x+h). Проведем через эти точки прямую (АВ). Рассмотрим выражение . Разность f(x+h)-f(x) равна расстоянию BL, а расстояние АL равно h. Отношение BL/AL - это тангенс ε угла - угла наклона прямой (АВ). Теперь представим себе, что величина h очень и очень мала. Тогда прямая (АВ) почти совпадет с касательной в точке х к графику функции y = f(x).

Итак, дадим определения.

Производной функции y = f(x) в точке х называется предел отношения  при h стремящемся к нулю. Пишут: 

Геометрический смысл производной – тангенс угла наклона касательной.

У производной есть еще и физический смысл. В начальных классах давалось определение скорости, как расстояние, деленное на время. Однако, в реальной жизни скорость, например, автомобиля, не постоянна на протяжении всего пути. Пусть путь – это некоторая функция от времени - S(t).Зафиксируем момент времени t. За небольшой промежуток времени от t до t+h автомобиль пройдет путь S(t+h)-S(t). За маленький промежуток времени скорость сильно не изменится и поэтому, можно использовать определение скорости, известное с начальной школы . А при h, стремящемся к нулю, это и будет производная.

Итак, физический смысл производной – мгновенная скорость в момент времени t.