Выведем формулы производных некоторых функций.

1. sin'(x) = cos(x).

Доказательство:

при h стремящемся к нулю, cos(h) стремится к 1, a sin(h) стремится к h. Строгое утверждение последнего утверждения выходит за рамки школьной программы, однако, чисто интуитивно можно в этом убедиться, посмотрев на следующий рисунок.

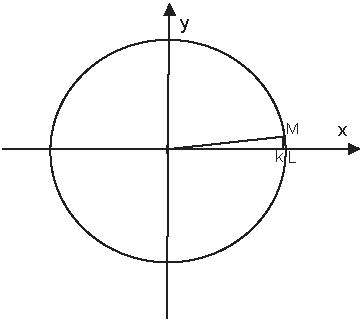
h – длина дуги МL, а sin(h) - это длина отрезка Mk. Когда угол очень маленький, эти величины почти совпадают.

Получаем:

2. cos'(x) = -sin(x).

Доказательство:

3. 

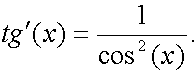
Доказательство:

Для доказательства этой формулы, будем использовать формулу производной от частного.

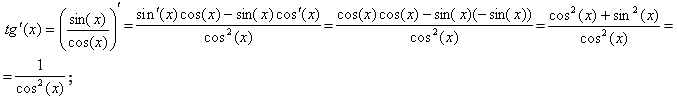
4. (ax)' = a.

Доказательство:

5. ln'(x) = 1/x

Эту формулу примем без доказательств.