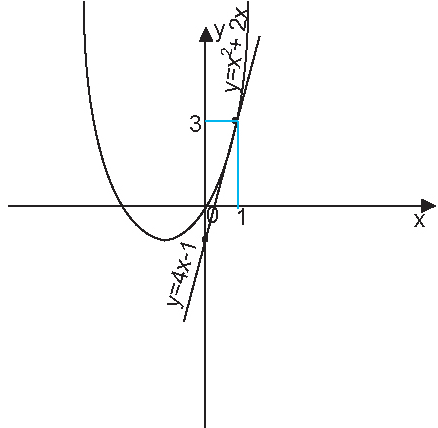Пусть у нас имеется график некоторой непрерывной и дифференцируемой на некотором отрезке функции y = f(x) и задана некоторая точка x₀ из этого отрезка.

Мы хотим написать уравнение касательной к графику функции в этой точке.

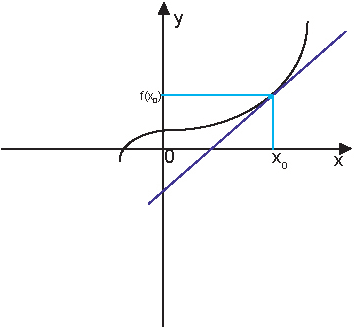
Касательная – это прямая, а уравнение прямой, как известно, выражается формулой y = kx+c, коэффициент k равен тангенсу угла между этой прямой и положительным направлением оси ОХ. 

Как, известно, геометрический смысл производной f'(x) – тангенс угла наклона касательной к графику функции f(x) в точке x. Значит в нашем случае k = f'(x₀).

Уравнение прямой примет вид y = f'(x₀)×x+c (*).

Неизвестным остается только один коэффициент – с. Найдем его следующим образом, раз это касательная в точке x₀, то она проходит через принадлежащую графику точку (x₀; f(x₀)). А раз прямая проходит через эту точку, значит, ее координаты удовлетворяют уравнению прямой.

Получаем уравнение:

f(x0) = f'(x0)×x₀+c;

c = f(x₀)-f'(x₀)×x₀.

Подставляя выражение для с в уравнение (*), получаем уравнение касательной к графику функции в точке x₀:

y = f'(x₀)×x+f(x₀)-f'(x₀)×x₀ = f'(x₀)(x-x₀)+f(x₀).

Пример.

Найти уравнение касательной к графику функции y = x²+2x в точке x₀ = 1.

Уравнение касательной имеет вид:

y = f'(x₀)(x-x₀)+f(x₀).

В нашем случае:

f'(x) = (x²+2x)' = 2x+2;

f'(x₀) = 2×1+2 = 4;

f(x0) = 1²+2×1 = 3.

Уравнение касательной запишется в виде:

y = 4×(x-1)+3 = 4x-4+3 = 4x-1;

y = 4x-1.