Содержание
1. Аннотация
2. Введение
3. Необходимые сведения
4. Исходные данные и обозначения
5. Вывод неизвестных коэффициентов системы уравнений
6. Реализация программы в среде Matlab
7. Примеры работы программы
8. Заключение
9. Список литературы
1. Аннотация.
Решение многих прикладных задач требует моделирования случайных векторов.
В работе приводится метод моделирования случайных векторов с одинаковым для всех координат одномерным законом распределения, заданной матрицей ковариации и математическим ожиданием составляющих. Для решения этой задачи используется система алгебраических уравнений с неизвестными коэффициентами. По соответствующему алгоритму разработана программа имитации значений векторов по заданной ковариационной матрице и математическим ожиданиям составляющих с треугольной матрицей преобразования. Изучена возможность покоординатных преобразований. Проведена проверка датчика псевдослучайных чисел системы MATLAB.
2. Введение.
Решение многих прикладных задач, таких как проведение модельных (машинных) экспериментов с помощью математического моделирования требует моделирования случайных векторов.
Предполагая определенные свойства объекта исследования и характеристики измерительной аппаратуры, исследователь имитирует результаты измерений, обрабатывает их тем или иным способом и сравнивает результат с заложенными ранее характеристиками объекта. Особенно необходимы такие эксперименты при решении некорректных обратных задач. При этом необходимо моделировать не только закономерное влияние на результат измерения свойств объекта исследования и аппаратные искажения, но и случайные погрешности измерений, т.е. случайные величины (вектора) с заданным законом распределения. Результат эксперимента, как правило, представляет собой массив отсчетов (вольтамперная характеристика, спектр излучения источника света, пространственное распределение яркости в изображении и т.п.).
Если отсчеты считать независимыми случайными величинами (их средние значения отражают какие-то закономерности, но к средним прибавлена случайная погрешность), то задача сводится к генерации значений независимых случайных величин (погрешностей) с нулевым средним и заданным законом распределения. В общем случае эту задачу легко решить с помощью генератора случайных чисел, равномерно распределенных в интервале (0,1), который встроен практически во все языки программирования высокого уровня.
Однако в реальных экспериментах, особенно если они выполняются быстро с помощью автоматизированных измерительных систем, погрешности измерения в различных экспериментальных точках могут быть коррелированны.
Ниже описывается метод моделирования случайных векторов с одинаковым для всех координат одномерным законом распределения, заданной матрицей ковариации и математическим ожиданием составляющих. Для решения этой задачи предлагается использовать систему алгебраических уравнений с неизвестными коэффициентами.
Алгоритм получения очередного случайного вектора ![]() заключается в следующем:
заключается в следующем:
— по заданным ковариационным матрицам и математическим ожиданиям составляющих случайных векторов вычисляются значения неизвестных коэффициентов системы линейных алгебраических уравнений;
— моделируется случайный вектор ![]() , координаты которого независимы и имеют заданное одномерное распределение;
, координаты которого независимы и имеют заданное одномерное распределение;
— с помощью указанной системы алгебраических уравнений получается случайный вектор ![]() .
.
Доказано, что при выполнении условий реализуемости системы линейных алгебраических уравнений закон распределения координат ![]() совпадает с одномерным законом распределения координат
совпадает с одномерным законом распределения координат ![]() , а значения коэффициентов ковариации любой пары
, а значения коэффициентов ковариации любой пары ![]() равны соответствующим элементам заданной матрицы коэффициентов ковариации.
равны соответствующим элементам заданной матрицы коэффициентов ковариации.
Моделирующая программа, использующая предложенный метод, определяет значения коэффициентов системы линейных алгебраических уравнений и проверяет выполнение условий реализуемости этой системы. В случае невыполнения условий реализуемости программа указывает на необходимость корректировки задаваемой матрицы коэффициентов ковариации.
Если указанные условия реализуемости выполнены, то программа позволяет выбрать количество (объем выборки) и размерность моделируемых векторов.
По окончании моделирования программа проверяет соответствие параметров закона распределения координат исходным требованиям, а также находит оценки для полученных в результате моделирования коэффициентов ковариации координат.
Программа реализована в вычислительной среде MATLAB.
3. Необходимые сведения.
Ниже приводятся необходимые сведения и определения из линейной алгебры и теории вероятности.
Математическое ожидание случайной величины обладает следующими свойствами.
- Математическое ожидание постоянной равно этой постоянной, т.е.
- Постоянный множитель можно вынести за знак математического ожидания, т.е.
- Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий, т.е.
- Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е.
![]() ,
, ![]() .
.
![]() .
.
![]() .
.
![]() .
.
Можно доказать, что для случайных величин ![]() и для независимых случайных величин
и для независимых случайных величин ![]() .
.
Дисперсия случайной величины обладает следующими свойствами.
- Дисперсия постоянной величины равно нулю, т.е.
- Постоянный множитель можно вынести за знак дисперсии возведя его в квадрат, т.е.
- Дисперсия суммы двух независимых случайных величин равно сумме их дисперсий, т.е.
![]() ,
, ![]() .
.
![]() .
.
![]() .
.
Можно доказать, что для случайных независимых величин![]()
Линейное преобразование случайных векторов. Предположим, что
![]() - случайный
- случайный ![]() - мерный вектор с математическим ожиданием
- мерный вектор с математическим ожиданием ![]() и корреляционной матрицей
и корреляционной матрицей ![]() . Введем матрицу преобразования
. Введем матрицу преобразования ![]() размером
размером ![]() и сформируем
и сформируем ![]() мерный вектор
мерный вектор
![]()
Можно показать справедливость следующих выражений
![]() ,
, ![]() .
.
![]() - вектор математического ожидания
- вектор математического ожидания ![]()
Если ![]() - случайный
- случайный ![]() - мерный вектор, координаты которого являются центрированными случайными величинами, то для выражения
- мерный вектор, координаты которого являются центрированными случайными величинами, то для выражения
![]()
справедливо ![]() .
.
4. Исходные данные и обозначения.
Исходными данными для поставленной задачи являются характеристики моделируемого случайного ![]() – мерного вектора
– мерного вектора ![]() :
:
 - ковариационная матрица,
- ковариационная матрица, ![]() ,
, ![]() ,
,
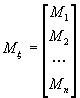 - вектор математического ожидания,
- вектор математического ожидания, ![]() .
.
В качестве вектора ![]() берется случайный вектор, координаты которого распределены по нормальному закону с параметрами:
берется случайный вектор, координаты которого распределены по нормальному закону с параметрами:
![]() - нулевой вектор математического ожидания, центрированная случайная величина равна самой случайной величине
- нулевой вектор математического ожидания, центрированная случайная величина равна самой случайной величине ![]() ,
,
![]() - дисперсия,
- дисперсия, 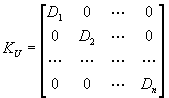 - ковариационная матрица.
- ковариационная матрица.
То есть координаты вектора независимы (отсутствует корреляция между компонентами вектора).
Вектор ![]() задается с помощью генератора случайных чисел, встроенного в систему MATLAB, для этих целей подходит функция
задается с помощью генератора случайных чисел, встроенного в систему MATLAB, для этих целей подходит функция
![]() ,
,
которая формирует массив, соразмерный с матрицей ![]() , элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1.
, элементами которого являются случайные величины, распределенные по нормальному закону с математическим ожиданием 0 и среднеквадратическим отклонением 1.
5. Вывод неизвестных коэффициентов системы линейных уравнений.
Координаты выходного вектора ![]()
![]() могут быть получены из нормально распределенных независимых случайных величин
могут быть получены из нормально распределенных независимых случайных величин ![]() - координат вектор
- координат вектор ![]() следующим образом:
следующим образом:
![]()
![]() или
или
 .
.
Можно переписать систему линейных уравнений в матричном виде:
![]() ,
,
где 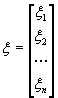 ,
,  ,
, 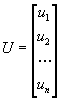 ,
, 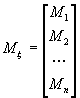 .
.
Найдем элементы матрицы ![]() , выразив их через элементы матриц
, выразив их через элементы матриц ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Так как ![]()
![]()
![]() , поэтому будем рассматривать
, поэтому будем рассматривать
центрированные случайные величины, прибавив к которым соответствующие математические ожидания, получим искомые координаты выходного вектора.
Для этого рассмотрим ковариацию двух случайных величин ![]()
![]() .
.
Так как
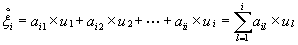 ,
,
аналогично
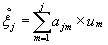 ,
,
используя приведенные выше свойства математического ожидания, и учитывая, что из исходных данных ![]() , получим
, получим
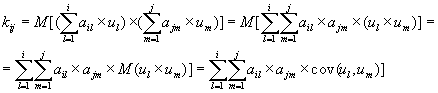 .
.
т.к. 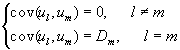 ,
,
таким образом, между элементами ковариационных матриц ![]() ,
,![]() , и элементами матрицы линейного преобразования
, и элементами матрицы линейного преобразования ![]() установлена следующая связь
установлена следующая связь
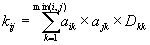 ,
,
или как было рассмотрено выше выражение в матричном виде
![]() .
.
Так как ![]() нижнетреугольная матрица (
нижнетреугольная матрица (![]() ) и
) и ![]() , то
, то

![]()
![]()
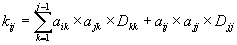
![]()
![]()
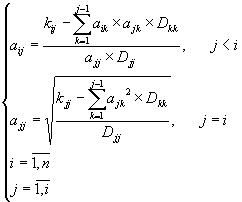 .
.
Эти рекуррентные соотношения позволяют найти элементы матрицы ![]()
по элементам ковариационных матриц, ![]() ,
, ![]() .
.
Рассмотрим двумерный массив ![]() , где каждый столбец рассматривается как переменная, а каждая строка – как наблюдение. Тогда выборочная матрица ковариации
, где каждый столбец рассматривается как переменная, а каждая строка – как наблюдение. Тогда выборочная матрица ковариации ![]() определяется следующим образом:
определяется следующим образом:
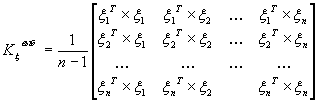
В системе MATLAB, присутствует функция ![]() , которая вычисляет матрицу ковариаций измерений (или выборочную матрицу ковариации).
, которая вычисляет матрицу ковариаций измерений (или выборочную матрицу ковариации).
Выборочная ковариационная матрица позволяет оценить соответствие моделируемых случайных векторов поставленной задачи.
6. Реализация программы в среде Matlab.
clear all;
n=3; размерность случайного вектора
N=100; количество наблюдений (объем выборки)
U=randn(n,N); генерация случайного вектора ![]()
cov_u = eye(n,n); ковариационная матрица ![]()
cov_ksi = 4*eye(n,n);
cov_ksi=[4 2 3 ; 2 9 6 ; 3 6 16]; ввод ковариационной матрицы ![]()
M_ksi=[-10; 0; 10]; ввод матрицы ![]()
M_ksi=zeros(n,1);
A=zeros(n,n);
проверка размерности ![]() и
и ![]()
if (size(cov_ksi) ~= n) | (size(M_ksi) ~= n)
error("Размерность матрицы сov_ksi или M_ksi не совпадает с n");
end
проверка корректности ![]()
for i=1:n,
if det(cov_ksi(1:i,1:i)) <= 0
error("Матрица сov_ksi не положительно определенна");
end
end
вычисление элементов матрицы ![]()
for i=1:n,
for j=1:i,
sum=0;
for k=1:(j-1),
sum=sum+A(i,k)*A(j,k)*cov_u(k,k);
end
if i==j
A(i,j)=sqrt((cov_ksi(i,j)-sum)/cov_u(j,j));
else
A(i,j)=(cov_ksi(i,j)-sum)/(A(j,j)*cov_u(j,j));
end
end
end
построение случайного вектора ![]()
for i=1:N,
ksi(:,i)=A*U(:,i)+M_ksi;
end
транспонирование матрицы случайных векторов ![]()
ksi_t=ksi";
вывод транспонированной матрицы в файл out.txt
save out.txt ksi_t –ASCII
disp("Матрица преобразований A");
A
disp("Выборка входных векторов U");
U
disp("Выходные векторы ksi");
ksi
disp("Исходн. матрица cov_ksi");
cov_ksi
построение выборочной ковариационной матрицы
disp("Выборочн. ков. матрица cov_ksi");
test_cov_ksi=cov(ksi_t)
проверка правильности преобразований
disp("Матрица cov_ksi (проверка правильности преобразований)");
A*cov_u*A"
построение гистограмм для входных и выходных векторов
figure(1);
hist(U",20);
xlabel("Интервалы");
ylabel(sprintf("Количество из g",N));
figure(2);
hist(ksi",50);
xlabel("Интервалы");
ylabel(sprintf("Количество из g",N));figure(1);
7. Примеры работы программы.
№ 1.
Входные данные:
размерность вектора ![]() ,
,
объем выборки ![]() ,
,
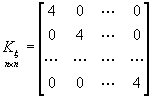 ,
, 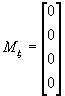 ,
,  ,
,  ,
,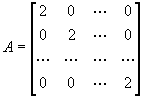 .
.
Гистограмма нормального распределения всех координат ![]()
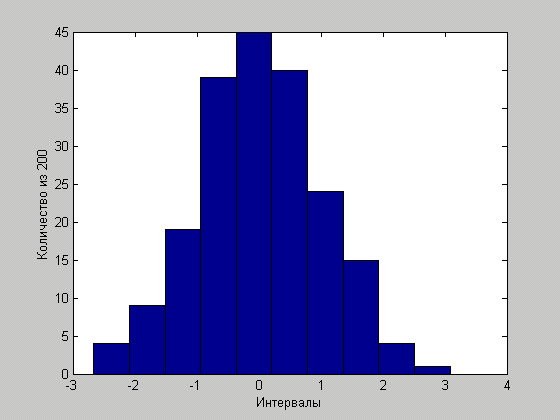
Гистограмма распределения всех координат ![]()
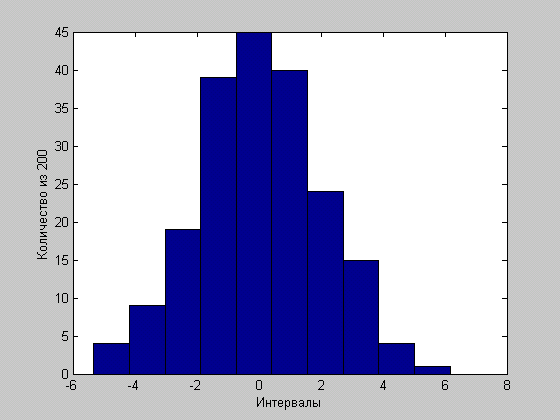
№ 2.
Входные данные:
размерность вектора ![]() ,
,
объем выборки ![]() ,
,
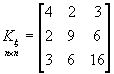 ,
, 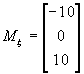 ,
, 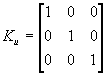 ,
,  .
.
Выходные данные:
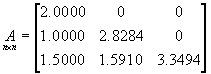 ,
, 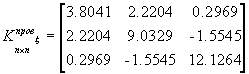
Как видно из полученных данных объем выборки недостаточен для оценки с помощью выборочной ковариационной матрицы полученного закона распределения координат, так как ковариационная матрица измерений значительно отличается от заданной. Поэтому увеличим объем выборки.
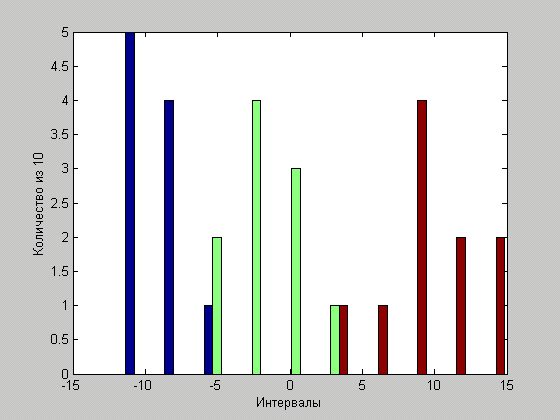
Гистограмма распределения координат ![]() для выборки
для выборки ![]()

Гистограмма распределения координат ![]() для выборки
для выборки ![]()
№ 3.
Входные данные:
размерность вектора ![]() ,
,
объем выборки ![]() ,
,
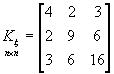 ,
, 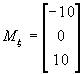 ,
, 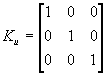 ,
,  .
.
Выходные данные:
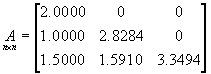 ,
, 
C увеличением объема выборок до ![]() элементы выборочной ковариационной матрицы отличаются от желаемых не более чем на 5%.
элементы выборочной ковариационной матрицы отличаются от желаемых не более чем на 5%.
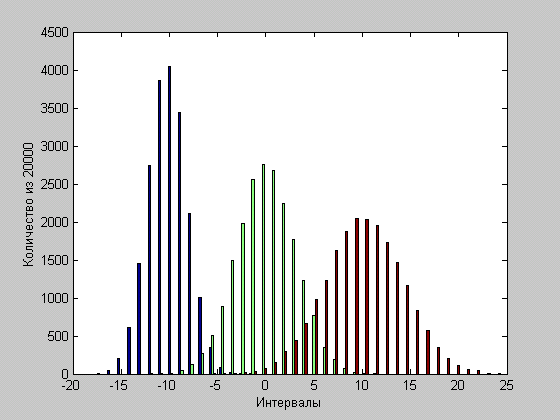
Гистограмма распределения координат ![]() для выборки
для выборки ![]()

Гистограмма распределения координат ![]() для выборки
для выборки ![]()
Заключение.
Итогом курсовой работы по теме “Моделирование значений случайных векторов” явилась разработка алгоритма моделирования значений случайных векторов, с одинаковым для всех координат одномерным законом распределения, заданной матрицей ковариаций и математическим ожиданием составляющих. Для достижения поставленной цели была изучена система MatLab, с помощью которой была создана моделирующая программа, позволяющая моделировать вектора по заданным параметрам. В программе присутствуют средства проверки соответствия полученных данных условиям поставленной задачи. Результаты работы программы представлены в виде графических данных и в виде сохранения массива полученных векторов в файл.
Список литературы.
1. Гусак А.А. Высшая математика. В 2-х т. Т. 2.:Учеб. Пособие для студентов вузов. – Мн.: ТетраСистемс, 1998. – 448 с.
2. Лазарев Ю.Ф. MatLAB 5.x – К.: Издательская группа BHV, 2000. – 384 с.
3. Потемкин В.Г. Система инженерных и научных расчетов MATLAB 5.x. В 2-х т. Т. 2 – М.: ДИАЛОГ-МИФИ, 1999. – 303 с.
4. Вентцель Е.С. Теория вероятностия. – М.: Государственное издательство физико-математической литературы, 1962. – 564 с.
Моделирование значений случайных векторов | ||
Система линейных уравнений:
или в матричной форме | Примеры работы программы. | |
Входные данные: размерность вектора объем выборки
| Выходные данные:
Объем выборки недостаточен для оценки полученных распределений координат, так как ковариационная матрица измерений значительно отличается от заданной. Поэтому увеличим объем выборки. | |
где
Рассматривая ковариацию случайных величин Далее выражаем неизвестные коэффициенты:
Эти рекуррентные соотношения позволяют найти элементы матрицы по элементам ковариационных матриц, Выборочная ковариационная матрица
| Гистограмма распределения координат
| Гистограмма распределения координат
|
Входные данные: размерность вектора объем выборки
| Выходные данные:
C увеличением объема выборок до не более чем на 5%. | |
Гистограмма распределения координат
| Гистограмма распределения координат | |
Документация по программе MonteCarlo.m
Входные данные:
N – количество моделируемых случайных векторов.
cov_ksi – ковариационная матрица элементов моделируемых случайных векторов.
M_ksi – матрица математического ожидания выходных векторов
n – размерность случайных векторов (вычисляется в программе по заданной ковариационной матрице).
Выходные данные:
ksi – матрица размерности ![]() , столбцами которой являются моделируемые случайные векторы.
, столбцами которой являются моделируемые случайные векторы.
out.txt – файл – распечатка случайных векторов ksi (сохраняется в той же директории, что и программа).


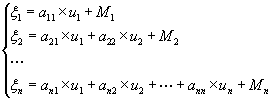 ,
,
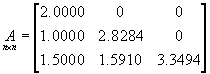 ,
,