1.147. Точка 1 тела, вращающегося с угловой скоростью ω, имеет в некоторый момент времени скорость v1. Найти для того же момента времени скорость v2 точки 2, смещенной относительно точки 1 на r12.

1.148. Тело совершает плоское движение в плоскости x, y. Центр масс тела С перемещается вдоль оси x с постоянной скоростью v0. В момент t=0 центр масс совпадал с началом координат О. Одновременно тело вращается в указанном на рис. 1.26 направлении со скоростью ω. Написать выражение для радиус-вектора r точки пересечения мгновенной оси вращения тела с плоскостью x, y.
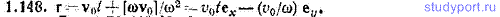
1.149. Балка массы m=300 кг и длины l=8,00 м лежит на двух опорах (рис. 1.27). Расстояния от концов балки до опор: l1=2,00 м, l2=1,00 м. Найти силы F1 и F2, с которыми балка давит на опоры.
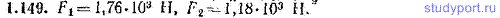
1.150. Лестница длины l=5,00 м и массы m=11,2 кг прислонена к гладкой стене под углом α=70° к полу (рис. 1.28). Коэффициент трения между лестницей и полом k=0,29. Найти: а) силу F1, с которой лестница давит на стену, б) предельное значение угла α0, при котором лестница начинает скользить.
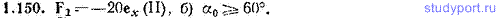
1.151. Протяженное тело произвольной формы брошено под некоторым углом к горизонту. Как движется центр масс тела в случае, если сопротивлением воздуха можно пренебречь?
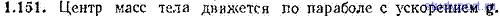
1.152. Невесомая нерастяжимая нить скользит без трения по прикрепленному к стене желобу (рис. 1.29) под действием грузов, массы которых m1=1,00 кг и m2=2,00 кг. С каким ускорением wC движется при этом центр масс грузов?

1.153. На рис. 1.30 изображены две частицы 1 и 2, соединенные жестким стержнем. Могут ли скорости частиц быть такими, как на рисунке? Частицы и скорости лежат в плоскости рисунка.
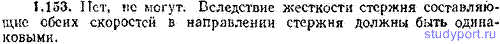
1.154. Две частицы (материальные точки) с массами m1 и m2 соединены жестким невесомым стержнем длины l. Найти момент инерции I этой системы относительно перпендикулярной к стержню оси, преходящей через центр масс.
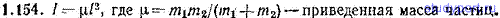
1.155. Найти момент инерции I однородного круглого прямого цилиндра массы m и радиуса R относительно оси цилиндра.

1.156. Плотность цилиндра длины l=0,100 м и радиуса R=0,0500 м изменяется с расстоянием от оси линейно от значения ρ1=500 кг/м3 до ρ2=3ρ1=1500 кг/м3 значения Найти: а) среднюю по объему плотность <ρ>v цилиндра; сравнить ее со средней по радиусу плотностью <ρ>r, б) момент инерции I цилиндра относительно оси; сравнить его с моментом инерции I’ однородного цилиндра такой же массы и размеров.
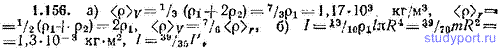
1.157. Найти момент инерции I однородного шара радиуса R и массы m относительно оси, проходящей через центр шара.

1.158. Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции I конуса относительно его оси.

1.159. Найти момент инерции тонкого однородного стержня длины l и массы m относительно перпендикулярной к стержню оси, проходящей через: а) центр масс стержня, б) конец стержня.
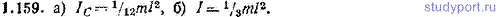
1.160. Найти момент инерции однородной прямоугольной пластинки массы m, длины a и ширины b относительно перпендикулярной к ней оси, проходящей через: а) центр пластинки, б) одну из вершин пластинки. Сравнить полученные результаты с ответом к предыдущей задаче.
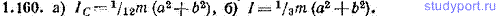
1.161. Найти момент инерции I однородного куба относительно оси, проходящей через центры противолежащих граней. Масса куба m, длина ребра a.

1.163. Найти момент инерции однородной пирамиды, основанием которой служит квадрат со стороной a, относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.
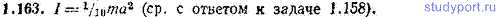
1.164. Найти отношение моментов инерции: а) пирамиды (с квадратным основанием) и конуса одинаковой высоты, плотности и массы, б) куба и шара одинаковой плотности и массы (у куба, как и у шара, момент инерции относительно любой проходящей через центр оси одинаков; см. задачу 1,162. Имеются в виду оси, проходящие через вершину и центр основания в случае а) и проходящие через центр в случае б).
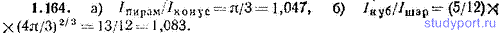
1.165. Найти главные моменты инерции тонкого однородного диска массы m и радиуса R. Иметь в виду, что вычисление целесообразно производить в полярных координатах r и φ.
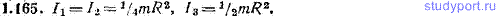
1.166. Вычислить момент инерции однородного круглого прямого цилиндра относительно оси, перпендикулярной к оси симметрии цилиндра и проходящей через его центр. Масса цилиндра m, радиус R, высота h. Сравнить полученный результат с ответами к задачам 1.159 и 1.165. Рассмотреть предельные случаи: R<<h и h<<R.


