1.187. Тонкий стержень длины l=1,00 м и массы m=0,600 кг может вращаться без трения вокруг перпендикулярной к нему горизонтальной оси, отстоящей от центра стержня на расстояние a=0,100 м. Стержень приводится в горизонтальное положение и отпускается без толчка с нулевой начальной скоростью. Определить: а) угловое ускорение стержня β0 и силу давления F0 на ось в начальный момент времени, б) угловую скорость ω и силу давления F на ось в момент прохождения стержнем положения равновесия.

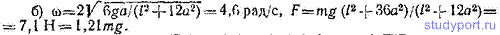
1.188. Тонкий стержень массы m = 0,200 кг и длины l=1,00 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. Трение в оси создает постоянный по модулю вращающий момент N. Выберем в качестве координаты, определяющей положение стержня, угол между стержнем и вертикалью, отсчитываемый от верхнего положения стержня. При значении этого угла, равном φ0 = 10,0°, стержень начинает самопроизвольно поворачиваться. Найти: а) угловую скорость ω стержня в момент, когда стержень проходит через нижнее положение, б) модуль момента импульса М стержня в этот момент.
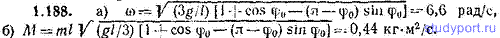
1.189. Столб высоты h=3,00 м и массы m=50,0 кг падает из вертикального положения на Землю. Определить модуль момента импульса M столба относительно точки опоры и скорость v верхнего конца столба в момент удара о Землю.
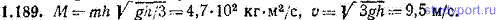
1.190. Линейка массы m=0,1200 кг и длины l=1,000 м лежит на гладком столе. По точке, отстоящей от центра линейки на расстояние a=40,0 см (рис. 1.35), наносится удар, при котором линейке сообщается импульс p=7,50*10-2 кг*м/с. Считая удар «мгновенным» и пренебрегая трением, а) найти расстояние x от центра линейки до точки О, которая не «почувствует» удара, б) определить, как движется линейка непосредственно после удара.
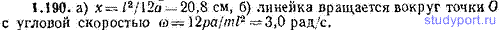
1.191. Однородный шарик помещен на плоскость, образующую угол α=30,0° с горизонтом (рис. 1.36). 1. При каких значениях коэффициента трения k шарик будет скатываться с плоскости без скольжения? 2. Полагая k=0,100, а) определить характер движения шарика, б) найти значения скоростей точек А, В и С шарика спустя t=1,00 с после начала движения.
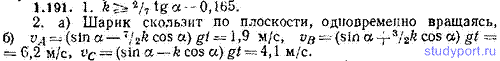
1.192. Однородному цилиндру сообщают начальный импульс, в результате чего он начинает катиться без скольжения вверх по наклонной плоскости со скоростью v0=3,00 м/с. Плоскость образует с горизонтом угол α=20,0°. а) Сколько времени t1 будет двигаться цилиндр до остановки? б) На какую высоту h поднимется цилиндр? в) Сколько времени t2 затратит цилиндр на скатывание вниз до исходного положения? г) Какую скорость v имеет цилиндр в момент возвращения в исходное положение? Сравнить полученные результаты с ответом к задаче 1.64.
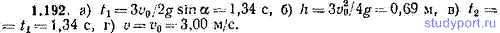
1.193. Решить задачу 1.192 в предположении, что на цилиндр действует постоянный по модулю момент силы трения качения . Масса цилиндра 1,00 кг, радиус 0,100 м. Помимо F указанных в предыдущей задаче величин, определить: д) какую работу А совершает сила трения качения на всем пути снизу вверх и обратно. Сравнить полученные результаты с ответами к предыдущей задаче и к задаче 1.65.
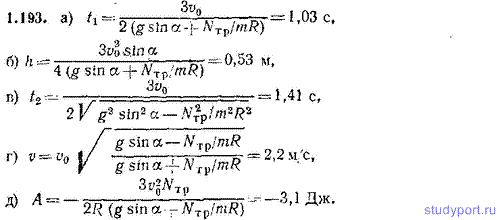
1.194. На горизонтальной плоскости лежит катушка, масса которой m=50,0 г, а момент инерции относительно ее оси I=5,00*10-6 . На катушку намотана практически невесомая и нерастяжимая нить (рис. 1.37). Радиус внешнего слоя витков r=2,00 см, радиус торцов катушки R=3,00 см. Коэффициент трения между катушкой и плоскостью k=0,200. За нить тянут с силой t. 1. Найти условие для силы F, при котором катушка катится по плоскости без скольжения. 2. Как ведет себя катушка, если сила F и угол α имеют значения: а) F=0,128 Н, α=30,0°, б) F=0,100 Н, α=48,2°, в) F=0,100 Н, α=30,0°, а) F=0,100 Н, α=60,0°. Для всех случаев определить wx - проекцию на ось х ускорения оси катушки.

1.195. Однородный сплошной цилиндр массы m=1,00 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис. 1.38). Цилиндр отпускают без толчка. а) За сколько времени t цилиндр опустится на расстояние h=50,0 см? б) Какое натяжение F испытывает при опускании цилиндра каждая из нитей?
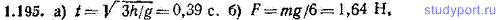
1.196. Блок радиуса R может вращаться вокруг своей оси с трением, характеризуемым вращающим моментом Nтр, который не зависит от скорости вращения блока. На блок намотана прикрепленная к нему одним концом практически невесомая нерастяжимая нить, к другому концу которой подвешен груз массы m (рис. 1.39). Груз отпускают без толчка и он начинает опускаться, раскручивая блок. Найти момент импульса M(t) этой системы тел относительно оси блока спустя время t после начала ее движения.
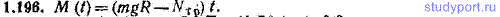
1.197. Найти момент импульса М относительно оси блока и кинетическую энергию T системы из предыдущей задачи в момент, когда скорость груза массы m равна v. Момент инерции блока принять равным I.
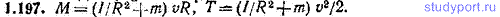
1.198. Имеются два одинаковых однородных диска. Один из них может вращаться без трения вокруг вертикальной фиксированной оси, проходящей через его центр. Этот диск первоначально неподвижен. Второй диск раскручивают, сообщив ему угловую скорость ω0, и роняют в горизонтальном положении на первый диск так, что край одного из дисков совпадает с центром другого. Придя в соприкосновение, диски мгновенно склеиваются. Определить: а) угловую скорость ω, с которой будет вращаться образовавшаяся система, б) как изменится кинетическая энергия дисков.
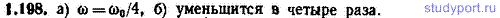
1.199. Горизонтально расположенный деревянный стержень массы m=0,800 кг и длины l=1,80 м может вращаться вокруг вертикальной оси, проходящей через его середину. В конец стержня попадает и застревает в нем пуля массы m'=3,00 г, летящая перпендикулярно к оси и к стержню со скоростью v=50,0 м/с. Определить угловую скорость ω, с которой начинает вращаться стержень.
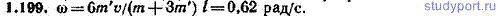
1.200. Решить задачу 1.199, заменив пулю пластмассовым шариком такой же массы и движущимся с той же скоростью. Удар считать абсолютно упругим. Определить: а) угловую скорость ω стержня, б) скорость v’ шарика после удара. Результат, полученный для ω, сравнить с ответом к задаче 1.199.
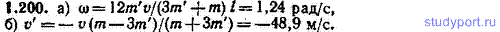
1.201. Горизонтальный диск массы m и радиуса R может вращаться вокруг вертикальной оси, проходящей через его центр. На краю диска стоит человек массы m'. Вначале диск и человек неподвижны. Затем человек начинает идти по краю диска со скоростью v' относительно диска. С какой скоростью ω вращается при этом диск относительно неподвижной системы отсчета? Размерами человека по сравнению с R можно пренебречь.

1.202. Тело вращается вокруг оси z с угловой скоростью ω=ω(t). На тело действует момент сил Nz=Nz(t). Написать выражение для работы, совершенной приложенными к телу силами за промежуток времени от t1 до t2.

1.203. Расположенный горизонтально однородный круглый цилиндр массы m = 10,00 кг вращается без трения вокруг своей оси под действием груза массы m’=1,000 кг, прикрепленного к легкой нерастяжимой нити, намотанной на цилиндр. Найти кинетическую энергию T системы спустя t=3,53 с после начала движения.
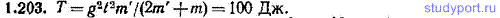
1.204. Вытащенное из колодца ведро с водой уронили, и оно стало опускаться вниз, раскручивая ворот. Трение в подшипниках ворота создает постоянный вращающий момент N=0,170 Н*м. Масса ведра с водой m=13,2 кг. Масса ворота m’=43,1 кг, радиус ворота r=12,8 см. Расстояние от края сруба до поверхности воды в колодце h=7,0 м. Определить: а) по какому закону изменяется со временем угловая скорость ω вращения ворота, б) натяжение веревки F во время опускания ведра, в) через сколько времени t ведро коснется воды в колодце, г) какую скорость v будет иметь ведро в конце падения, д) какую работу А совершают силы трения за время падения ведра. Ворот считать сплошным однородным цилиндром. Массой и толщиной веревки, массой рукоятки ворота, а также сопротивлением воздуха пренебречь.
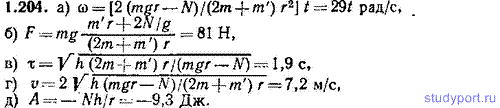
1.205. Расположенный горизонтально однородный цилиндр радиуса R может вращаться вокруг оси, совпадающей с его геометрической осью. Трение в оси создает не зависящий от скорости вращения момент Nтр. К цилиндру прикреплена точечная масса m’ (рис. 1.40). Цилиндр устанавливают так, чтобы масса оказалась на уровне оси, и отпускают без толчка. Определить, при каком значении m’: а) цилиндр придет во вращение, б) сделав 1/4 оборота, цилиндр остановится.
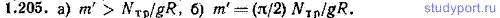
1.206. Диск массы m и радиуса R первоначально вращается вокруг своей оси с угловой скоростью ω. Под действием внешних сил диск останавливается. Чему равна работа А внешних сил?


