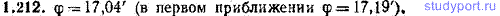1.207. Однородный цилиндр массы m и радиуса R вращается вокруг своей оси. Угловая скорость цилиндра изменяется за время t от значения ω1 до значения ω2. Какую среднюю мощность <Р> развивают силы, действующие на цилиндр?

1.208. Ротор некоторого агрегата снабжен дисковым тормозом. Этот тормоз состоит из двух дисков радиуса R = 150 мм, один из которых закреплен на конце оси ротора, а другой, лишенный возможности вращаться, может прижиматься к первому с силой F=100 Н. Тормоз включают в момент, когда ротор вращается по инерции со скоростью ω=50,0 рад/с (трением в подшипниках можно пренебречь). Момент инерции ротора вместе с укрепленным на нем диском тормоза I=0,628 кг*м2. Коэффициент трения между поверхностями дисков не зависит от их относительной скорости и равен k=0,250. Считая, что сила F равномерно распределяется по поверхности дисков, определить, сколько оборотов N успеет сделать ротор до остановки.

1.209. Гироскоп в виде однородного диска радиуса R=8,00 см вращается вокруг своей оси с угловой скоростью ω=3,00*102 рад/с. Угловая скорость прецессии гироскопа ω’=1,00 рад/с. Определить расстояние l от точки опоры до центра масс гироскопа. Моментом инерции оси гироскопа пренебречь.

1.210. Гироскоп массы m = 1,000 кг, имеющий момент инерции I=4,905*10-3 кг*м2, вращается с угловой скоростью 100,0 рад/с. Расстояние от точки опоры до центра масс l=5,00 см. Угол между вертикалью и осью гироскопа α=30,0°. Найти: а) модуль угловой скорости прецессии ω’, б) модуль углового ускорения гироскопа β.
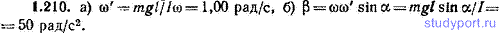
1.211. Поместив начало координат в точку опоры гироскопа и направив ось z вверх по вертикали, а) найти угловое ускорение β гироскопа из предыдущей задачи; считать, что в начальный момент ось гироскопа находилась в плоскости х, z; б) вычислив скалярное произведение ωβ, определить, как направлен вектор β.
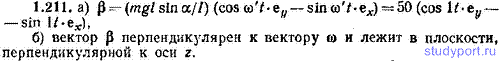
1.212. Гироскоп, вращающийся вокруг оси симметрии с угловой скоростью ω=100 рад/с, прецессирует в поле земного тяготения с угловой скоростью ω’=1,00 рад/с. Угол между вертикалью и осью гироскопа α = 30,0°. Определить угол φ между осью симметрии и направлением угловой скорости гироскопа Ω (см. задачу 1.49). Решить задачу методом последовательных приближений, положив φ в нулевом приближении равным нулю.