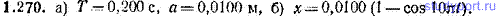1.251. Частица совершает гармоническое колебание с амплитудой а и периодом Т. Найти: а) время t1 за которое смещение частицы изменяется от 0 до а/2, б) время t2, за которое смещение изменяется от а/2 до а.
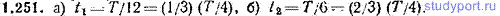
1.252. Частица колеблется вдоль оси x по закону x=0,100 sin 6,28t (м). Найти среднее значение модуля скорости частицы <v>: а) за период колебания Т, б) за первую 1/8 часть Т, в) за вторую 1/8 часть Т. Сопоставить полученные значения.
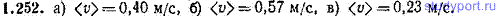
1.253. Для частицы из задачи 1.252 найти среднее значение вектора скорости <v>: а) за период колебания Т, б) за первую четверть Т, в) за вторую четверть Т.
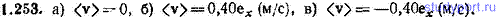
1.254. Как, зная амплитуду смещения а и амплитуду скорости найти частоту гармонического колебания ω?

1.255. Как, зная амплитуду скорости vm и амплитуду ускорения ωm, найти амплитуду а и частоту ω гармонического колебания?

1.256. Горизонтальная платформа совершает в вертикальном направлении гармоническое колебание x=a cos ωt. На платформе лежит шайба из абсолютно неупругого материала. а) При каком условии шайба будет отделяться от платформы? б) В каком положении находится и в каком направлении движется платформа в момент отрыва от нее шайбы? в) На какую высоту h будет подниматься шайба над ее положением, отвечающем среднему положению платформы, в случае, если a=20,0 см, ω=10,0 с-1?

1.257. Найти средние значения sin2x и cos2x на промежутке от α до α+nπ (α - произвольный угол, n - целое число).

1.258. Чему равна при гармоническом колебании работа А квазиупругой силы за время, равное периоду колебаний?

1.259. а) Найти уравнение, связывающее значения импульса px=mx со значениями координаты x одномерного гармонического осциллятора. Масса осциллятора m, частота ω, амплитуда колебания а. б) Нарисовать кривую, описываемую этим уравнением. в) Выразить площадь S, ограниченную этой кривой, через энергию осциллятора Е.
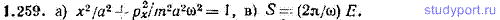
1.260. Определить частоту ω малых колебаний частицы из задачи 1.92, возникающих в том случае, если частицу сместить в радиальном направлении из положения устойчивого равновесия. Массу частицы принять равной m.
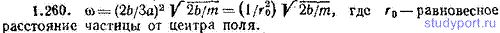
1.261. а) При какой длине l период колебаний математического маятника будет равен 1 с? б) Чему равен период колебаний T математического маятники длины l = 1 м?
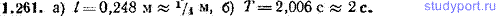
1.262. Роль физического маятника выполняет тонкий стержень, подвешенный за один из его концов. а) При какой длине стержня период колебаний этого маятника будет равен 1 с? б) Чему равен период колебаний m при длине стержня в 1 м?
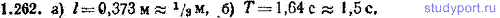
1.263. На каком расстоянии х от центра нужно подвесить тонкий стержень заданной длины l, чтобы получить физический маятник, колеблющийся с максимальной частотой? Чему равно значение ωmax этой частоты?
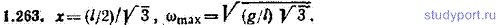
1.264. Найти закон, по которому изменяется со временем натяжение F нити математического маятника, совершающего колебание φ=φmcos ωt. Масса маятника равна m, длинаl.
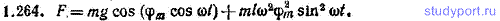
1.265. В неподвижной кабине лифта качается маятник. Вследствие обрыва троса кабина начинает падать с ускорением g. Как ведет себя маятник относительно кабины лифта, если в момент обрыва троса он а) находился в одном из крайних положений, б) проходил через положение равновесия?
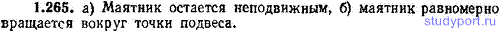
1.266. В кабине лифта подвешен маятник, период колебаний которого, когда лифт неподвижен, равен T0. а) Каков будет период T колебаний маятника, если лифт станет опускаться с ускорением, равным ¾ g? б) С каким ускорением ω нужно поднимать лифт для того, чтобы период колебаний маятника был равен ½ T0?

1.267. В кабине самолета подвешен маятник. Когда самолет летит без ускорения, маятник качается с частотой ω0. а) Какова будет частота ω колебаний маятника, если самолет летит с ускорением w, направление которого образует с направлением вниз по вертикали угол α? б) Найти ω для случая, когда w=g и α=π/2.
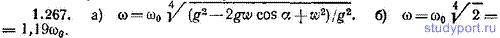
1.268. Найти период колебаний T математического маятника, длина подвеса которого l равна радиусу Земли RЗ. Сравнить полученный результат с ответом к задаче 1.246, п. г).
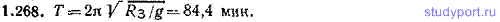
1.269. Физический маятник устанавливают так, что его центр масс располагается над точкой подвеса. Из этого положения маятник начинает двигаться без трения с нулевой начальной скоростью. В момент прохождения через нижнее положение угловая скорость маятника достигает значения φmax. Найти собственную частоту ω0 малых колебаний этого маятника.

1.270. Шарик массы m=50,0 г подвешен на пружина жесткости k=49,3 Н/м. Шарик поднимают до такого положения, при котором пружина не напряжена, и отпускают без толчка. Пренебрегая трением и массой пружины, а) найти период T и амплитуду а возникших колебаний, б) направив ось х вниз и совместив точку х=0 с начальным положением шарика, написать уравнение движения шарика.