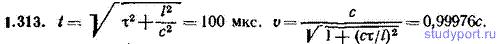1.294. Согласуется ли с принципами специальной теории относительности представление о теле в виде шара радиуса R=1,00 м, вращающегося вокруг своей оси с угловой скоростью ω=3,30*108 рад/с?
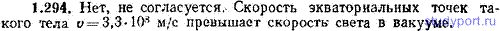
1.295. Согласуется ли с принципами специальной теории относительности представление об электроне как о вращающемся вокруг своей оси однородном шарике массы m=0,911*10-30 кг (масса электрона) и радиуса R=2,82*10-15 м (классический радиус электрона), обладающем собственным моментом импульса M=0,913*10-34 кг*м2/с (вытекающее из квантовой теории и подтвержденное экспериментально значение собственного момента импульса электрона)?
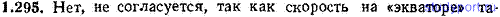
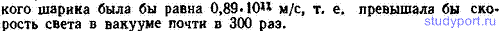
1.296. В системе К некоторое событие произошло в точке с координатами (1,00; 1,00; 1,00) в момент t=1,00 с. Определить координаты и время этого события в системе К', движущейся относительно К в направлении совпадающих осей х и х' со скоростью v0=0,800 с.
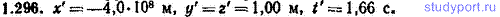
1.297. Имеются два одинаковых стержня. Стержень 1 покоится в. системе отсчета К1, стержень 2 покоится в системе отсчета К2. Системы движутся друг относительно друга вдоль совпадающих осей х. Стержни параллельны этим осям. Какой стержень будет короче: а) в системе K1, б) в системе К2?

1.298. Какую продольную скорость v нужно сообщить стержню для того, чтобы его длина стала равной половине длины, которую он имеет в состоянии покоя?

1.299. а) Чему равно относительное приращение длины стержня Δl/l0, если ему сообщить скорость v=0,1с в направлении, образующем с осью покоившегося стержня угол α? б) Вычислить для значений α, равных: 0, 45, 90°,
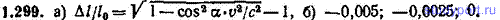
1.300. Решить задачу 1.299 для скорости v = 0,9c.
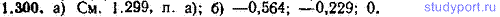
1.301. В системе К', относительно которой стержень покоится, он имеет длину l' = 1,00 м и образует с осью х' угол α'=45°. Определить в системе К длину стержня l и угол α, который стержень образует с осью х. Относительная скорость систем равна v0=0,500c.
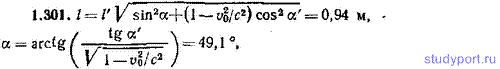
1.302. Неподвижное тело произвольной формы имеет объем V0. Чему равен объем V того же тела, если оно движется со скоростью v0=0,866с?

1.303. Суммарная поверхность неподвижного тела, имеющего форму куба, равна S0. Чему равна поверхность S того же тела, если оно движется в направлении одного из своих ребер со скоростью v=0,968с?

1.304. Имеются две системы отсчета К и К', относительная скорость которых неизвестна. Параллельный оси х' стержень, движущийся относительно системы К' со скоростью v'x=0,100c, имеет в этой системе длину l' = 1,10 м. В системе К длина стержня l=1,00 м. Найти скорость vx стержня в системе К и относительную скорость систем v0.
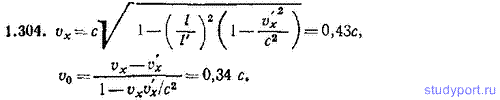
1.305. Имеется двое одинаковых часов. Часы 1 покоятся в системе отсчета K1, часы 2 покоятся в системе отсчета K2. Системы движутся друг относительно друга. Какие часы идут быстрее: а) в системе K1, б) в системе K2?

1.306. Двое одинаковых синхронизированных часов укреплены на концах стержня с собственной длиной l0. При каком значении l0 разность показаний часов Δt определенная наблюдателем, движущимся параллельно стержню со скоростью v0=0,600c окажется равной: а) 1,000 мкс, б) 1,000 с?
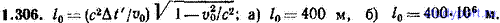
1.307. Решить предыдущую задачу для v0=0,999с.
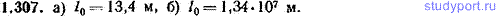
1.308. На концах двух стержней собственной длины l0= 10,00 м укреплены одинаковые синхронизированные друг с другом часы (рис. 1.50). Стержни приведены в движение с относительной скоростью v0=c/2. В момент, когда часы 1 и 1' находятся друг против друга, стрелки обоих часов показывают нулевой отсчет. Определить: а) показания τ1 и τ'2 часов 1 и 2' в момент, когда они поравняются друг с другом, б) показания τ2 и τ'1 часов 2 и 1' в момент, когда они поравняются друг с другом, в) показания τ2 и τ'2 часов 2 и 2' в момент, когда они поравняются друг с другом.
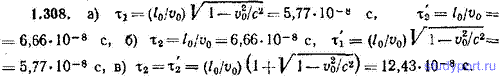
1.309. Собственное время жизни некоторой частицы оказалось равным τ=1,00-10-6 с. Чему равен интервал Δs между рождением и распадом этой частицы?

1.310. С какой скоростью v должна лететь частица относительно системы отсчета К для того, чтобы промежуток собственного времени Δτ был в 10 раз меньше промежутка Δt, отсчитанного по часам системы K?

1.311. За промежуток времени Δt=1,000 с, отсчитанный по часам некоторой системы отсчета К, частица, двигаясь прямолинейно и равномерно, переместилась из начала координат системы К в точку с координатами x=y=z=1,50*108 м. Найти промежуток собственного времени частицы Δτ, за который произошло это перемещение.
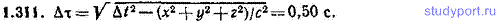
1.312. Собственное время жизни нестабильной элементарной частицы равно τ. Считая движение частицы прямолинейным и равномерным, определить путь l, который она пройдет до распада в системе отсчета, в которой время жизни частицы равно t.

1.313. Собственное время жизни нестабильной элементарной частицы, называемой мюоном, τ=2,2 мкс. Определить время жизни t мюона в системе отсчета, в которой он проходит до распада путь l=30 км. Считая движение мюона прямолинейным и равномерным, найти скорость мюона v.