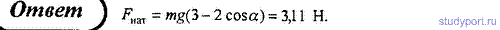81. Тело массой m = 5 кг поднимают с ускорением a = 2 м/с2. Определить работу силы в течение первых пяти секунд.

82. Автомашина массой m = 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути. Определить: 1) работу, совершаемую двигателем автомашины на пути 5 км, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.

83. Определите работу, совершаемую при подъеме груза массой m = 50 кг по наклонной плоскости с углом наклона α = 30° к горизонту на расстояние s = 4 м, если время подъема t = 2 с, а коэффициент трения f = 0,06.
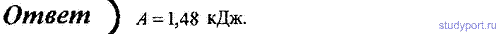
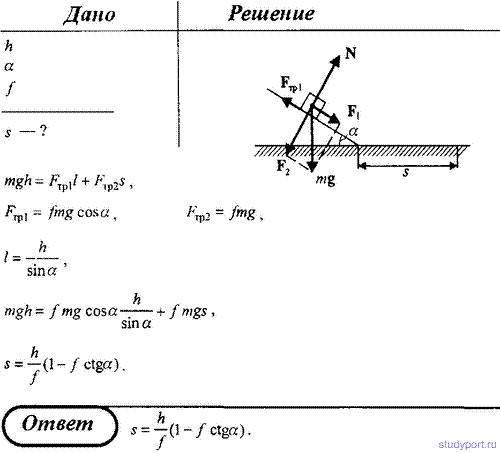
84. Тело скользит с наклонной плоскости высотой h и углом наклона α к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным f, определить расстояние s, пройденное толом на горизонтальном участке, до полной остановки.
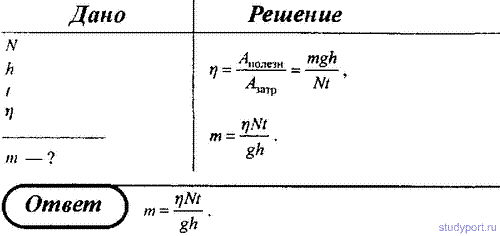
85. Насос мощностью N используют для откачки нефти с глубины h. Определить массу жидкости, поднятой за время t, если КПД насоса равен η.
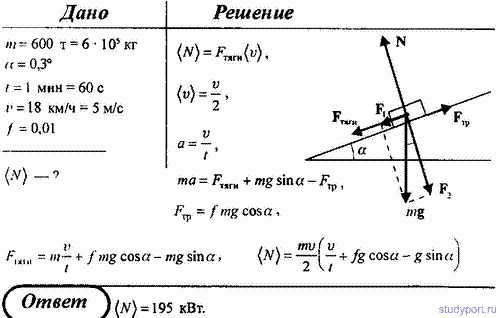
86. Поезд массой m = 600 т движется под гору с уклоном α = 0,3° и за время t = 1 мин развивает скорость v = 18 км/ч. Коэффициент трения f = 0,01. Определить среднюю мощность локомотива.
87. Автомобиль массой т = 1,8 т спускается при выключенном двигателе с постоянной скоростью v = 54 км/ч по уклону дороги (угол к горизонту α = 3°). Определите, какой должна быть мощность двигателя автомобиля, чтобы он смог подниматься на такой же подъем с той же скоростью.

88. Материальная точка массой m = 1 кг двигалась под действием некоторой силы согласно уравнению s = A – B*t + C*t2 – D*t3 (B = 3 м/с, C = 5 м/с2, D = 1 м/с3). Определить мощность N, затрачиваемую на движение точки за время, равное 1 с.

89. Ветер действует на парус площадью S с силой F = A*S*ρ*(v0 – v)2/2, где А – некоторая постоянная; ρ – плотность воздуха; v0 – скорость ветра; v – скорость лодки. Определить скорость лодки при максимальной мгновенной мощности ветра.

90. Тело массой m поднимается без начальной скорости с поверхности Земли под действием силы F, изменяющейся с высотой подъема y по закону F = -2mg(l - Ay) (где А — некоторая положительная постоянная), и силы тяжести mg , Определите: 1) весь путь подъема; 2) работу силы F на первой трети пути подъема. Поле силы тяжести считать однородным.
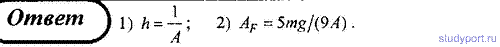
91. Тело массой m начинает двигаться под действием силы F = 2*t*i + 3*t2*j, где i и j – соответственно единичные векторы координатных осей x и y. Определить мощность N(t), развиваемую силой в момент времени t.

92. Тело массой m = 5 кг падает с высоты h = 20 м. Определить сумму потенциальной и кинетической энергий тела в точке, находящейся от поверхности Земли на высоте h1 = 5 м. Трением тела о воздух пренебречь. Сравнить энергию с первоначальной энергией тела.

93. Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом p = 100 кг * м/с и кинетической энергией T = 5 00 Дж Определите: 1) с какой начальной высоты тело падало, 2) массу тела.
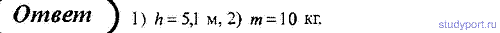
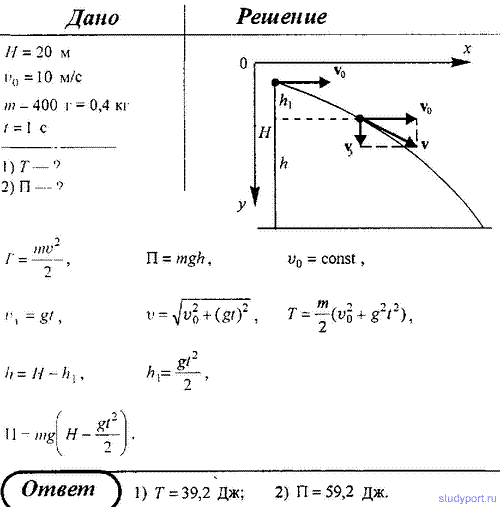
94. С башни высотой H = 20 м горизонтально со скоростью v0 = 10 м/с, брошен камень массой m = 400 г. Пренебрегая сопротивлением воздуха, определить для момента времени t = 1 с после начала движения: 1) кинетическую энергию; 2) потенциальную энергию.
95. Автомашина массой m = 2000 кг останавливается за t = 6 c, пройдя расстояние s = 30 м. Определить: 1) начальную скорость автомобиля; 2) силу торможения.

96. Материальная точка массой m = 20 г движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением. К концу пятого оборота после начала движения кинетическая энергия материальной точки оказалась равной 6,3 мДж. Определить тангенциальное ускорение.

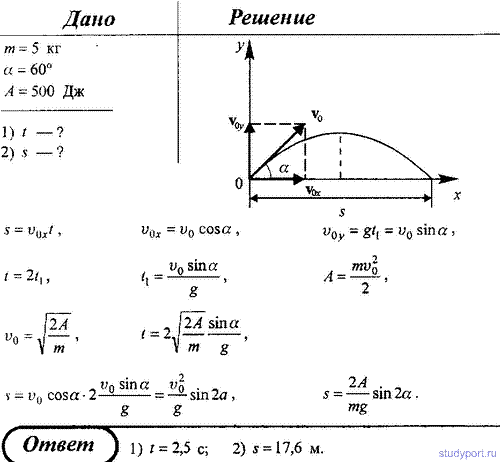
97. Ядро массой m = 5 кг бросают под углом α = 60° к горизонту, совершая при этом работу 500 Дж. Пренебрегая сопротивлением воздуха, определить: 1) через какое время ядро упадет на землю; 2) какое расстояние по горизонтали оно пролетит.
98. Тело массой m = 0,5 кг бросают со скоростью v0 = 10 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определите кинетическую Т, потенциальную П и полную Е энергии тела: 1) через t = 0,4 с после начала движения; 2) в высшей точке траектории.
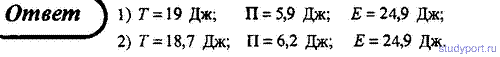
99. Тележка проходит расстояние s = 300 м под гору с уклоном α = 5° и продолжает двигаться в гору с тем же уклоном. Принимая коэффициент трения f постоянным и равным 0,05, определите расстояние x, на которое поднимается тележка.

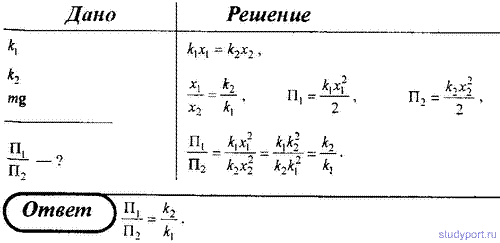
100. К нижнему концу пружины жесткостью k1 присоединена другая пружина жесткостью k2, к концу которой прикреплена гиря. Пренебрегая массой пружины, определить отношение потенциальных энергий пружин.
101. Тело массой m = 0,4 кг скользит с наклонной плоскости высотой h = 10 см и длиной l = 1 м. Коэффициент трения тела на всем пути f = 0,04. Определите: 1) кинетическую энергию тела у основания плоскости; 2) путь, пройденный телом на горизонтальном участке до остановки.