160. Человек массой m = 60 кг, стоящий краю горизонтальной платформы массой M = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мни-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определитe, с какой частотой n2 будет тогда вращаться платформа.
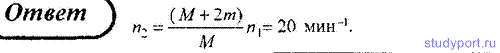
161. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

162. Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом R = 1 м, и массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n1 = 10 мин^-1, переходит к её центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить работу, совершаемую человеком при переходе от края платформы к её центру.

164. К проволоке из углеродистой стали длиной l = 1,5 м и диаметром d = 2,1 мм подвешен груз массой m = 110 кг. Принимая для стали модуль Юнга E = 216 ГПа и предел пропорциональности σn = 330 МПа, определить: 1) какую долю первоначальной длины составляет удлинение проволоки при этом грузе; 2) превышает приложенное напряжение или нет предел пропорциональности.

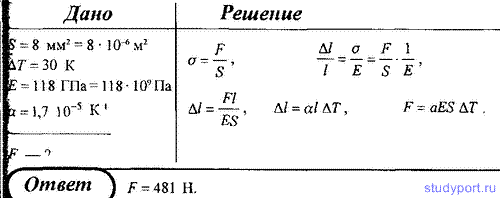
165. Медная проволока сечением S = 8 мм2 под действием растягивающей силы удлинилась на столько, на сколько она удлиняется при нагревании на 30 К. Принимая для меди модуль Юнга E = 118 ГПа и коэффициент линейного расширения а = 1,7*10-5 К-1, определить числовое значение этой силы.
166. Резиновый шнур длиной 40 см и внутренним диаметром 8 мм натянут так, что удлинился на 8 см. Принимая коэффициент Пуассона для резины равным 0,5, определить внутренний диаметр натянутого шнура.

167. Определите работу, которую необходимо затратить, чтобы сжать пружину на 15 см, если известно, что сила пропорциональна деформации и под действием силы 20 Н пружина сжимается на 1 см.

168. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа A = 6,9 Дж. Длина стержня l = 1 м, площадь поперечного сечения S = 1 мм2, модуль Юнга для алюминия E = 69 ГПа.
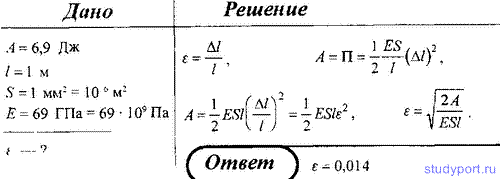
169. Определите объемную плотность потенциальной энергии упруго-растянутого медного стержня, если относительное изменение длины стержня ε = 0,01 и для меди модуль Юнга E = 118 ГПа.
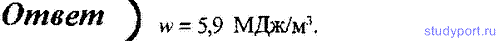
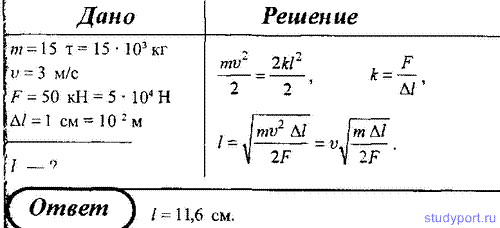
170. Два вагона (масса каждого m = 15 т) движутся навстречу друг другу со скоростью v = 3 м/с и сталкиваются между собой. Определить сжатие пружины буферов вагона, если известно, что сила пропорциональна деформации, и под действием силы F = 50 кН пружина сжимается на Δl = 1 см.