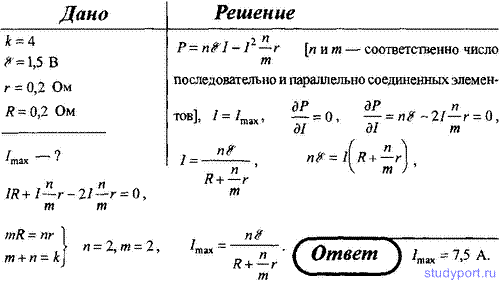
96. Даны четыре элемента с ЭДС ε = 1,5 В и внутренним сопротивлением r = 0,2 Ом. Как нужно соединить эти элементы, чтобы получить от собранной батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R = 0,2 Ом? Определить максимальную силу тока.
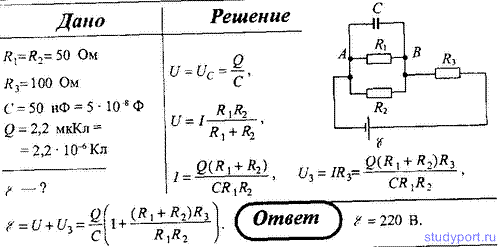
97. На рисунке R1 = R2 = 50 Ом, R3 = 100 Ом, С = 50 нФ. Определите ЭДС источника, пренебрегая его внутренним сопротивлением, если заряд на конденсаторе Q = 2,2 мкКл.
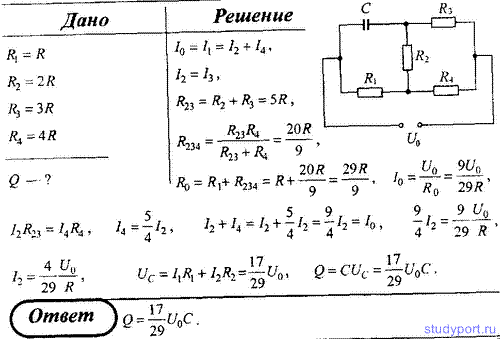
98. На рисунке R1 = R, R2 = 2R, R3 = 3R, R4 = 4R. Определите заряд на конденсаторе.
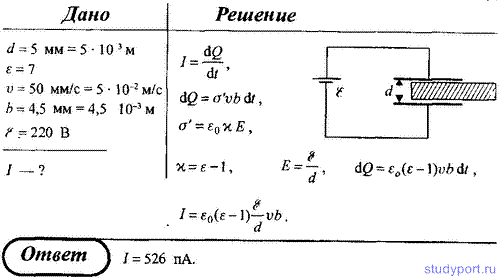
99. В плоский конденсатор, расстояние между пластинами которого d = 5 мм, вдвигают стеклянную пластинку (ε = 7) с постоянной скоростью v = 50 мм/с. Ширина пластины b = 4,5 мм, ЭДС батареи ε = 220 В. Определите силу тока в цепи батареи, подключенной к конденсатору.
100. Два источника тока с ЭДС ε1 = 2 В и ε2 = 1,5 В и внутренними сопротивлениями r1 = 0,5 Ом и r2 = 0,4 Ом включены параллельно сопротивлению R = 2 Ом. Определить силу тока через это сопротивление.

101. На рисунке ε1 = ε2 = ε3, R1, = 48 Ом, R2 = 24 Ом, падение напряжения U2 на сопротивлении R2 равно 12 В. Пренебрегая внутренним сопротивлением элементов, определите: 1) силу тока во всех участках цепи; 2) сопротивление R3.
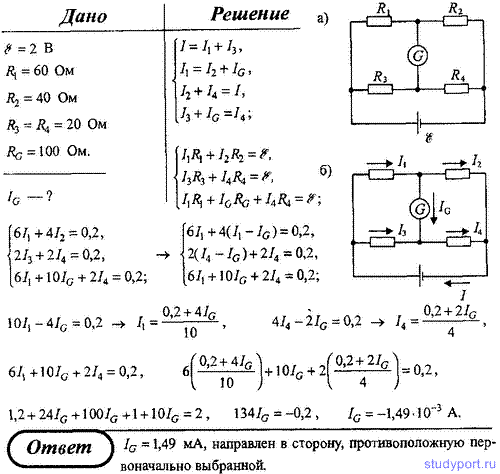
102. На рисунке Е = 2 В, R1 = 60 Ом, R2 = 40 Ом, R3 = R4 = 20 Ом и RG = 100 Ом. Определить силу тока IG через гальванометр.
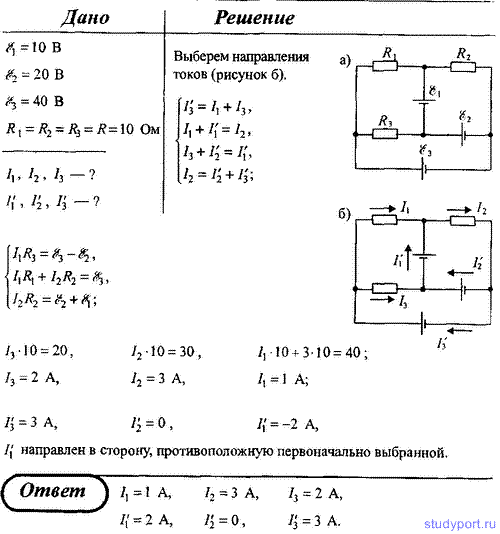
103. На рисунке Е1 = 10 В, Е2 = 20 В, Е3 = 40 В, а сопротивления R1 = R2 = R3 = R = 10 Ом. Определить силу токов, протекающих через сопротивления (I) и через источник ЭДС (I`). Внутреннее сопротивление источников ЭДС не учитывать.