3.1. Найти момент инерции J и момент импульса L земного шара относительно оси вращения.
Решение:
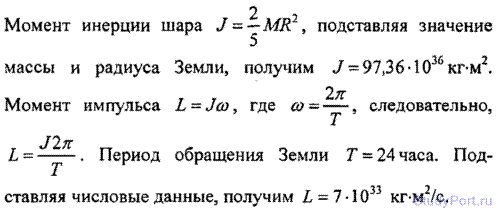
3.2. Два шара одинакового радиуса R = 5 см закреплены на концах невесомого стержня. Расстояние между шарами r = 0,5 м. Масса каждого шара m = 1 кг. Найти: а) момент инерции J1 системы относительно оси, проходящей через середину стержня перпендикулярно к нему; б) момент инерции J2 системы относительно той же оси, считая шары материальными точками, массы которых сосредоточены в их центрах; в) относительную ошибку б = (J1 - J2)/ J2, которую мы допускаем при вычислении момента инерции системы, заменяя величину J1 величиной J2.
Решение:
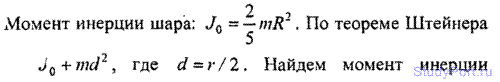

3.3. К ободу однородного диска радиусом R = 0,2 м прило касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения Mтр=98,1 Н*м. Найти массу m дисков, если известно, что диск вращается с угловым ускоре е = 100 рад/с2.
Решение:


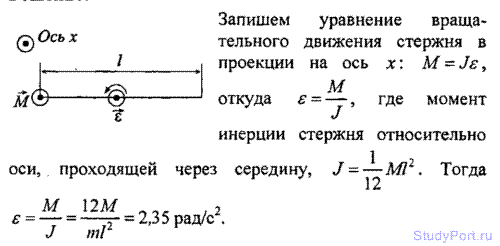
3.4. Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением е вращается стержень, если на него действует момент сил М = 98,1 мН*м?
Решение:
3.5. Однородный диск радиусом R = 0,2 м и массой m = 0,5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости w вращения диска от времени t дается уравнением w = А + Bt, где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь.
Решение:

3.6. Маховик, момент инерции которого J = 63,6кгм2 враща с угловой скоростью w = 31,4 рад/с. Найти момент сил тор М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.
Решение:
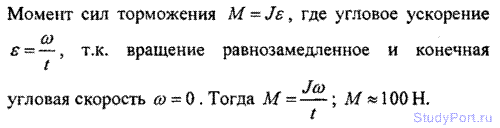
3.7. К ободу колеса радиусом 0,5м и массой m = 50 кг при касательная сила F = 98,1 Н. Найти угловое ускорение s колеса. Через какое время t после начала действия силы колесо будет иметь частоту вращения n = 100 об/с? Колесо считать однородным диском. Трением пренебречь.
Решение:


3.8. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения, T = 14,7Н. Какую частоту вра n будет иметь маховик через время t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.
Решение:

3.9. Маховое колесо, момент инерции которого J = 245 кг л, вращается с частотой n = 20 об/с. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения и число оборотов N, которое сделало колесо до полной остановки после прекра действия сил. Колесо считать однородным диском.
Решение:

З.10. Две гири с массами m1 =2 кг и m2 =1кг соединены нитью, перекинутой через блок массой m = 1 кг. Найти ускорение а, с которым движутся гири, и силы натяжения T1 и T2 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Решение:

3.11. На барабан массой m0=9кг намотан шнур, к концу которого привязан груз массой m = 2 кг. Найти ускорение а гру. Барабан считать однородным цилиндром. Трением прене.
Решение:

3.12. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Найти момент инерции J барабана, если известно, что груз опускается с ускорением а = 2,04 м/с2.
Решение:

3.13. На барабан радиусом R = 20 см, момент инерции кото J = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом hQ = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию WK груза в момент удара о пол и силу натяжения нити T. Трением пренебречь.
Решение:
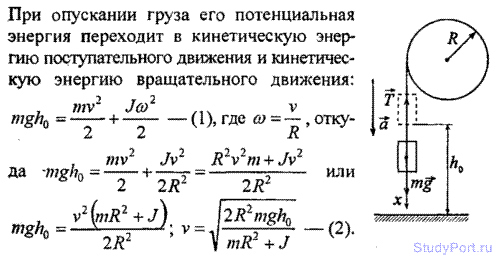

3.14. Две гири с разными массами соединены нитью, переки через блок, момент инерции которого J = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока = 98,1 Нм. Найти разность сил натяжения нити T1 -T2 по обе стороны блока, если известно, что блок вращается с угловым ускорением e = 2,36 рад/с2. Блок считать однородным диском.
Решение:

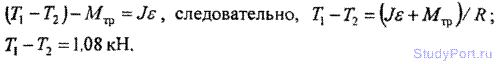
3.15. Блок массой m = 1 кг укреплен на конце стола ( см. рис. и задачу 2.31). Гири 1 и 2 одинаковой массы m1=m2=1кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол к = 0,1 . Найти ускорение а, с которым движутся гири, и силы натяжения T1 и T2 нитей. Блок считать однород диском. Трением в блоке пренебречь.
Решение:

3.16. Диск массой m = 2 кг катится без скольжения по гори плоскости со скоростью v = 4 м/с. Найти кинети энергию Wk диска.
Решение:

3.17. Шар диаметром D = 6 см и массой m = 0,25 кг катится без скольжения по горизонтальной плоскости с частотой враще n = 4 об/с. Найти кинетическую энергию WK шара.
Решение:
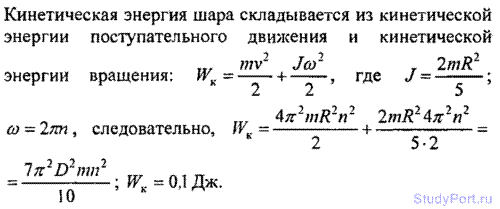
3.18. Обруч и диск одинаковой массы m1 = m2 катятся без скольжения с одной и той же скоростью v. Кинетическая энер обруча WKl =4кгсм. Найти кинетическую энергию Wk2 диска.
Решение:
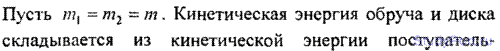

3.19. Шар массой m = 1 кг катится без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку v = 10 см/с, после удара u = 8 см/с. Найти количество теплоты Q, выделившееся при ударе шара о стенку.
Решение:

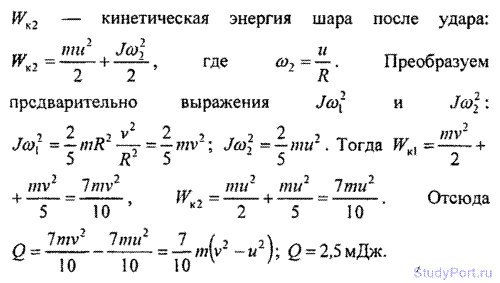
3.20. Найти относительную ошибку б, которая получится при вычислении кинетической энергии WK катящегося шара, если не учитывать вращения шара.
Решение:


