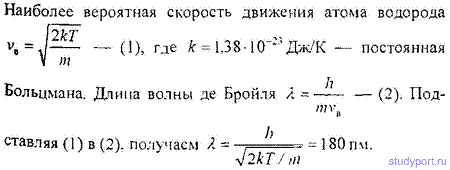19.21. Между электродами фотоэлемента предыдущей задачи приложена задерживающая разность потенциалов U = 1 В. При какой предельной длине волны λ0 падающего на катод света начинается фотоэффект?
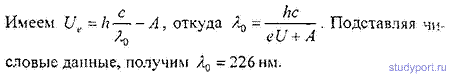
19.22. На рисунке показана часть прибора, с которым П. Н. Лебедев производил свои опыты по измерению светового давления. Стеклянная крестовина, подвешенная на тонкой нити заключена в откачанный сосуд и имеет на концах два легких кружка из платиновой фольги. Один кружок зачернен, другой оставлен блестящим. Направляя свет на один из кружков и измеряя угол поворота нити (для зеркального отсчета служит зеркальце S), можно определить световое давление. Найти световое давление P и световую энергию E , падающую от дуговой лампы в единицу времени на единицу площади кружков. При освещении блестящего кружка отклонение зайчика a = 76 мм по шкале, удаленной от зеркальца на расстояние b = 1200мм. Диаметр кружков d = 5 мм. Расстояние от центра кружка до оси вращения l = 9,2 мм. Коэффициент отражения света от блестящего кружка ρ = 0,5. Постоянная момента кручения нити (M = kα) k = 2,2*10-11 Н*м/рад.


19.23. В одном из опытов П. Н. Лебедева при падении света на зачерненный кружок (ρ = 0) угол поворота нити был равен α = 10'. Найти световое давление Р и мощность N падающего света. Данные прибора взять из условия задачи 19.22.
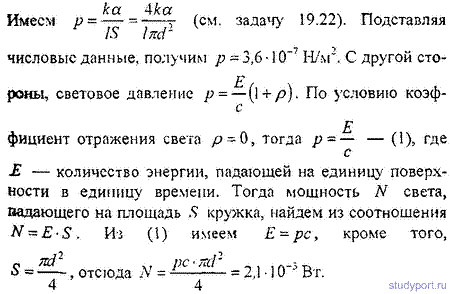
19.24. В одном из опытов П.Н.Лебедева мощность падающего на кружки монохроматического света (λ = 560нм) была равна N = 8,33 мВт. Найти число фотонов I , падающих в единицу времени па единицу площади кружков, и импульс силы FΔτ, сообщенный единице площади кружков за единицу времени, для значений ρ, равных: 0; 0,5; 1. Данные прибора взять из условия задачи 19.22.

19.25. Русский астроном Ф. А. Бредихин объяснил форму кометных хвостов световым давлением солнечных лучей. Найти световое давление Р солнечных лучей на абсолютно черное тело, помешенное на таком же расстоянии от Солнца, как и Земля. Какую массу m должна иметь частица в кометном хвосте, помещенная на этом расстоянии, чтобы сила светового давления на нее уравновешивалась силой притяжения частицы Солнцем? Площадь частицы, отражающую все падающие на нее лучи, считать равной S = 0,5 * 10-12 м2. Солнечная постоянная K = 1,37 кВт/м2.
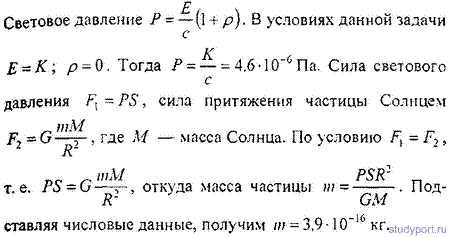
19.26. Найти световое давление Р на стенки электрической 100-ваттной лампы. Колба лампы представляет собой сферический сосуд радиусом r = 5 см. Стенки лампы отражают 4% и пропускают 6% падающего на них света. Считать, что вся потребляемая мощность идет на излучение.

19.27. На поверхность площадью S = 0,01 м2 в единицу времени падает световая энергия E = 1,05Дж/с. Найти световое давление Р в случаях, когда поверхность полностью отражает и полностью поглощает падающие на нее лучи.

19.28. Монохроматический пучок света (λ=490нм), падая по нормали к поверхности, производит световое давление Р = 4.9 мкПа. Какое число фотонов I падает в единицу времени на единицу площади этой поверхности? Коэффициент отражения света ρ = 0,25.

19.29. Рентгеновские лучи с длиной волны λ0 = 70,8 пм испытывают комптоновское рассеяние на парафине. Найти длину волны λ рентгеновских лучей, рассеянных в направлениях: а) φ = π/2 ; б) φ = π .

19.30. Какова была длина волны λ0 рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом φ = 60° длина волны рассеянного излучения оказалась равной λ = 25,4 пм?
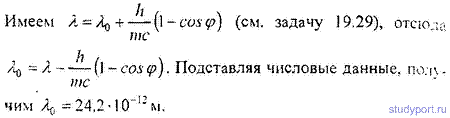
19.31. Рентгеновские лучи с длиной волны λ0 = 20 пм испытывают комптоновское рассеяние под углом φ = 90°. Найти изменение Δλ длины волны рентгеновских лучей при рассеянии, а также энергию We и импульс электрона отдачи.

19.32. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния φ = π/2 . Найти энергию W и импульс p рассеянного фотона.
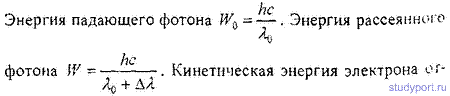

19.33. Энергия рентгеновских лучей ε = 0,6 МэВ. Найти энергию We электрона отдачи, если длина волны рентгеновских лучей после комптоновского рассеяния изменилась на 20%.

19.34. Найти длину волны де Бройля λ для электронов, прошедших разность потенциалов U1 = 1 В и U2 = 100 В.


19.35. Решить предыдущую задачу для пучка протонов.

19.36. Найти длину волны де Бройля λ для: a) электрона, движущегося со скоростью v = 106 м/с; б) атома водорода, движущегося со средней квадратичной скоростью при температуре T = 300 К; в) шарика массой m = 1 г, движущегося со скоростью v = 1 см/с.

19.37. Найти длину волны де Бройля λ для электрона, имеющего кинетическую энергию: а) W1 = 10 кэВ; б) W2 = 1 МэВ.
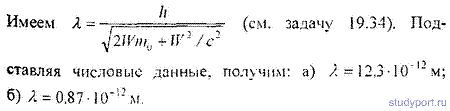
19.38. Заряженная частица, ускоренная разностью потенциалов U = 200 В. имеет длину волны де Бройля λ = 2,02 пм. Найти массу m частицы, если ее заряд численно равен заряду электрона.

19.39. Составить таблицу значений длин волн де Бройля для электрона, движущегося со скоростью v, равной: 2*108; 2.2*108; 2.4*108: 2.6*108; 2.8*108 м/с.

19.40. α-частица движется пo окружности радиусом r = 8.3 мм в однородном магнитном поле, напряженность которого H = 18,9 кА/м. Найти длину волны де Бройля λ для α-частицы.


19.41. Найти длину волны де Бройля λ для атома водорода, движущегося при температуре T = 293 К с наиболее вероятной скоростью.