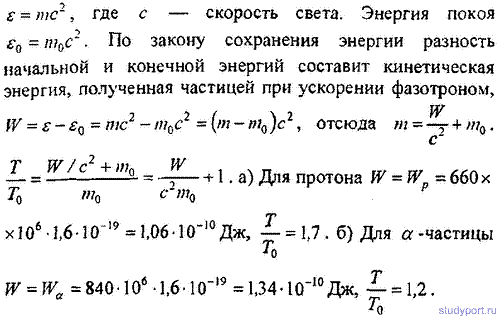23.21. Решить предыдущую задачу для: а) дейтонов, б) α-частиц.

23.22. Ионный ток в циклотроне при работе с α-частицами I = 15 мкА. Во сколько раз такой циклотрон продуктивнее массы m = 1 г радия?


23.23. Максимальный радиус кривизны траектории частиц в циклотроне R = 50 см; магнитная индукция поля В = 1 Тл. Какую постоянную разность потенциалов U должны пройти протоны, чтобы получить такое же ускорение, как в данном циклотроне?

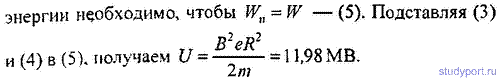
23.24. Циклотрон дает дейтоны с энергией W = 7MэB. Магнитная индукция поля циклотрона В = 1,5 Тл. Найти минимальный радиус кривизны R траектории дейтона.

23.25. Между дуантами циклотрона радиусом R = 50 см приложена переменная разность потенциалов U = 75 кВ с частотой ν = 10МГц. Найти магнитную индукцию В поля циклотрона, скорость v и энергию W вылетающих из циклотрона частиц. Какое число оборотов n делает заряженная частица до своего вылета из циклотрона? Задачу решить для дейтонов, протонов и α-частиц.


23.26. До какой энергии W можно ускорить α-частицы в циклотроне, если относительное увеличение массы частицы k = (m-m0)/m0 не должно превышать 5%?

23.27. Энергия дейтонов, ускоренных синхротроном, W = 200 МэВ. Найти для этих дейтонов отношение m/m0 (где m — масса движущегося дейтона и m0 — его масса покоя) и скорость v.

23.28. В фазотроне увеличение массы частицы при возрастании ее скорости компенсируется увеличением периода ускоряющего поля. Частота разности потенциалов, подаваемой на дуанты фазотрона, менялась для каждого ускоряющего цикла от ν0 = 25 МГц до ν = 18,9 МГц. Найти магнитную индукцию В поля фазотрона и кинетическую энергию W вылетающих протонов.
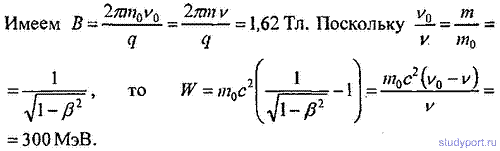
23.29. Протоны ускоряются в фазотроне до энергии W = 660 МэВ, α-частицы — до энергии W = 840 МэВ. Для того чтобы скомпенсировать увеличение массы, изменялся период ускоряющего поля фазотрона. Во сколько раз необходимо было изменить период ускоряющего поля фазотрона (для каждого ускоряющего цикла) при работе: а) с протонами; б) с α-частицами?