2.21(2.21). Шарик В веса Р подвешен к неподвижной точке А посредством нити АВ и лежит на поверхности гладкой сферы радиуса r; расстояние точки А от поверхности сферы АС = d, длина нити АВ = l, прямая АО вертикальна. Определить натяжение Т нити и реакцию Q сферы. Радиусом шарика пренебречь.

Ответ: Т = Рl/(d+r), Q = Pr/(d+r).

2.22(2.22). Однородный шар веса 10 Н удерживается в равновесии двумя тросами АВ и CD, расположенными в одной вертикальной плоскости и составляющими один с другим угол 150°. Трос АВ наклонен к горизонту под углом 45°. Определить натяжение тросов.

Ответ: Т_B = 19,3 Н, Т_C = 14,1 Н.

2.23(2.23). Котел с равномерно распределенным по длине весом Р = 40 кН и радиуса R = 1 м лежит на выступах каменной кладки. Расстояние между стенками кладки l = 1,6 м. Пренебрегая трением, найти давление котла на кладку в точках A и В.

Ответ: N_a = N_b = 33,3 кН.

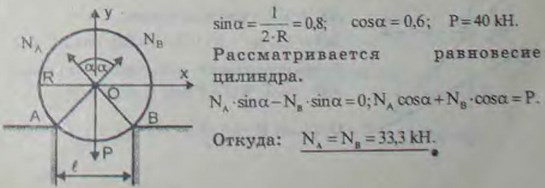
2.24(2.24). Вес однородного трамбовочного катка равен 20 кН, радиус его 60 см. Определить горизонтальное усилие Р, необходимое для перетаскивания катка через каменную плиту высоты 8 см, в положении, указанном на рисунке.

Ответ: Р = 11,5 кН.

2.25(2.25). Однородный стержень АВ веса 160 Н, длины 1,2 м подвешен в точке С на двух тросах АС и СВ одинаковой длины, равной 1 м. Определить натяжения тросов.

Ответ: Натяжение каждого троса равно 100 Н.

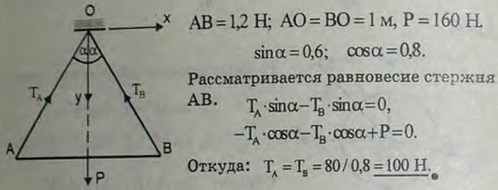
2.26(2.26). Однородный стержень АВ прикреплен к вертикальной стене посредством шарнира А и удерживается под углом 60° к вертикали при помощи троса ВС, образующего с ним угол 30°. Определить величину и направление реакции R шарнира, если известно, что вес стержня равен 20 Н.

Ответ: R = 10 Н, угол (R, АС) = 60°.

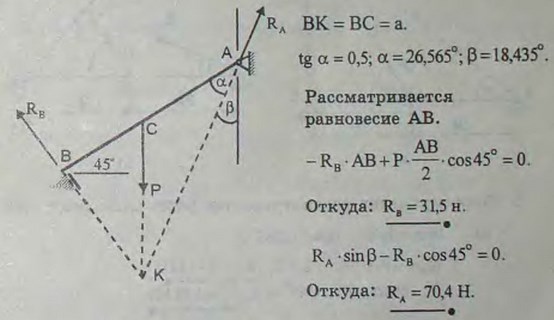
2.27(2.27). Верхний конец А однородного бруса АВ, длина которого 2 м, а вес 50 Н, упирается в гладкую вертикальную стену. К нижнему концу В привязан трос ВС. Найти, на каком расстоянии АС нужно прикрепить трос к стене для того, чтобы брус находился в равновесии, образуя угол BAD = 45°. Найти натяжение Т троса и реакцию R стены.

Ответ: АС = AD = 1,41 м, Т = 56 Н, R = 25 Н.

2.28(2.28). Оконная рама АВ, изображенная на рисунке в разрезе, может вращаться вокруг горизонтальной оси шарнира А и своим нижним краем В свободно опирается на уступ паза. Найти реакции опор, если дано, что вес рамы, равный 89 Н, приложен к середине С рамы и AD = BD.

Ответ: R_a = 70,4 Н, R_B = 31,5 Н.

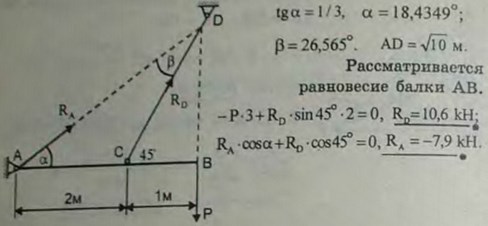
2.29(2.29). Балка АВ поддерживается в горизонтальном положении стержнем CD; крепления в A, С и D шарнирные. Опреде лить реакции опор А и D, если на конце балки действует вертикальная сила F = 5 кН. Размеры указаны на рисунке. Весом пренебречь.

Ответ: R_A = 7,9 кН, R_D = 10,6 кН.

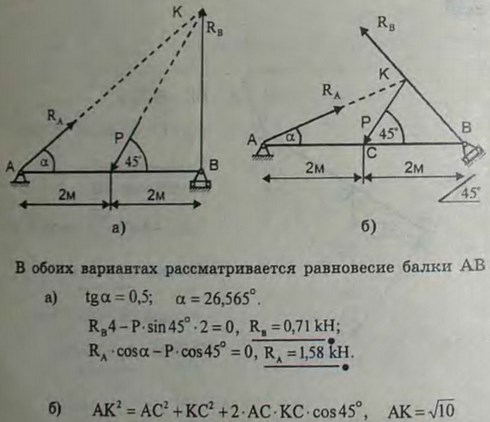
2.30(2.30). Балка АВ шарнирно закреплена на опоре A; у конца В она положена на катки. В середине балки, под углом 45° к ее оси, действует сила Р = 2 кН. Определить реакции опор для случаев а и б, взяв размеры с рисунков и пренебрегая весом балки.

Ответ: а) R_A = 1,58 кН, R_B = 0,71 кН;

б) R_A= 2,24 кН, R_B = 1 кН.

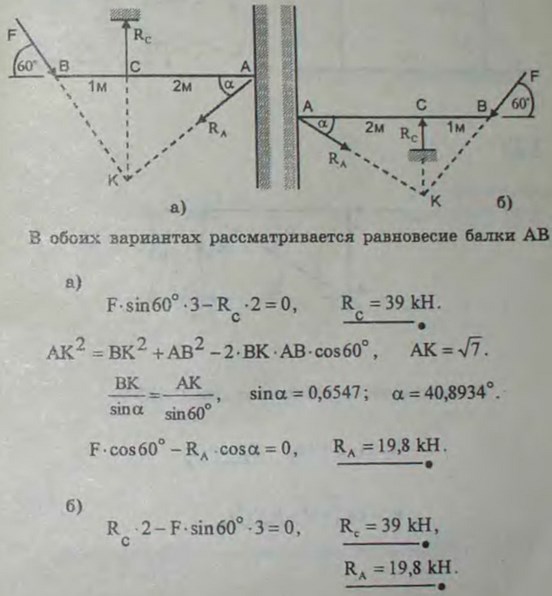
2.31(2.31). На рисунках изображены балки АВ, удерживаемые в горизонтальном положении вертикальными стержнями CD. На концах балок действуют силы F = 30 кН под углом 60° к горизонту. Взяв размеры с рисунков, определить усилия S в стержнях CD и давления Q балок на стену, если крепления в А, С и D шарнирные. Весом стержней и балок пренебречь.

Ответ: a) S = 39 кН, Q = 19,8 кН; б) S = 39 кН, Q = 19,8 кН.

2.32(2.32). Электрический провод АСВ натянут между двумя столбами так, что образует пологую кривую, стрела провисания которой CD = f = 1 м. Расстояние между столбами АВ = l = 40 м. Вес провода Q = 0,4 кН. Определить натяжения провода: Т_С в средней точке, Т_А и Т_B на концах. При решении задачи считать, что вес каждой половины провода приложен на расстоянии l/4 от ближнего столба.

Ответ: Т_C = Ql/8f = 2 кН; T_A = T_B = 2,01 кН.

2.33(2.33). Для рамы, изображенной на рисунке, определить опорные реакции R_A и R_D, возникающие при действии горизонтальной силы Р, приложенной в точке В. Весом рамы пренебречь.

Ответ: R_A = Р ν(5/2), R_D = P/2.

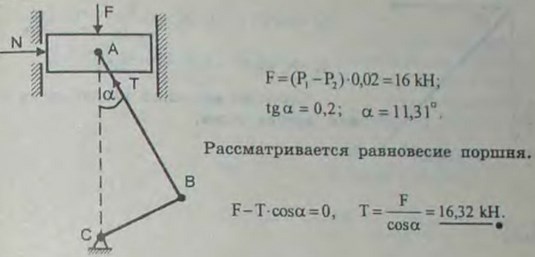
2.34(2.34). В двигателе внутреннего сгорания площадь поршня равна 0,02 м², длина шатуна АВ = 30 см, длина кривошипа ВС = 6 см. Давление газа в данный момент над поршнем равно P₁ = 1000 кПа, под поршнем Р₂ = 200 кПа. Найти силу Т, действующую со стороны шатуна АВ на кривошип ВС, вызванную перепадом давлений газа, если угол АВС = 90°. Трением между поршнем и цилиндром пренебречь.

Ответ: Т= 16 кН.

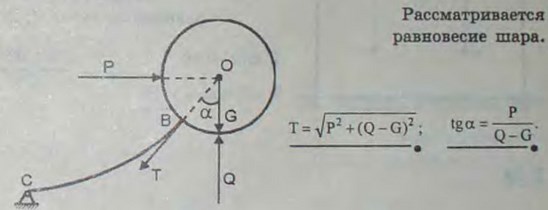
2.35(2.35). Воздушный шар, вес которого равен G, удерживается в равновесии тросом ВС. На шар действуют подъемная сила Q и горизонтальная сила давления ветра, равная Р. Определить натяжение троса в точке В и угол α.

Ответ:    Т = ν(P² + (Q - G)²), α = —= arctg P/(Q - G).

2.36(2.36). Для сжатия цементного кубика М по четырем граням пользуются шарнирным механизмом, в котором стержни АВ, ВС и CD совпадают со сторонами квадрата ABCD, а стержни 1, 2, 3, 4 равны между собой и направлены по диагоналям того же квадрата; две равные по модулю силы Р прикладываются к точкам А и D, как показано на рисунке. Определить силы N₁, N₂, N₃, N₄, сжимающие кубик, и усилия S₁, S₂, S₃ в стержнях АВ, ВС и CD, если величина сил, приложенных в точках А и D, равна 50 кН.

Ответ: N₁ = N₂ = N₃ = N₄ = 70,7 кН. Растягивающие усилия: S₁ = S₂ = S₃ =^: 50 кН.

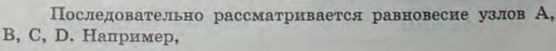
2.37(2.37). Два трамвайных провода подвешены к поперечным проволочным канатам, из которых каждый прикреплен к двум столбам. Столбы расставлены вдоль пути на расстоянии 40 м друг от друга. Для каждого поперечного каната расстояния АК = KL = LB = 5 м; КС = LD = 0,5 м. Пренебрегая весом проволочного каната, найти натяжения Т₁, Т₂ и Т₃ в частях его АС, CD и DB, если вес 1 м провода равен 7,5 Н.

Ответ: Т₁ = Т₃ = 3,015 кН, Т2 = 3 кН.

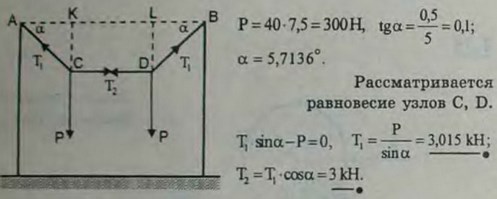
2.38(2.38). К шарниру А стержневого шарнирного четырехугольника ABDC, сторона CD которого закреплена, приложена сила Q = 100 Н под углом BAQ = 45°. Определить величину силы R,приложенной в шарнире В под углом ABR = 30° таким образом, чтобы четырехугольник ABDC был в равновесии, если углы CAQ = 90°, DBR = 60°.

Ответ: R = 163 Н.

2.39(2.39). Стержневой шарнирный многоугольник состоит из четырех равных стержней; концы А и Е шарнирно закреплены; узлы В, С и О нагружены одинаковой вертикальной нагрузкой Q. В положении равновесия угол наклона крайних стержней к горизонту α = 60°. Определить угол β наклона средних стержней к горизонту.

Ответ: β = 30°.

2.40(2.40). Для трехшарнирной арки, показанной на рисунке, определить реакции опор А и В, возникающие при действии горизонтальной силы Р. Весом арки пренебречь.

Ответ: R_a = R_b = P√2/2