2.41(2.41). Прямолинейный однородный брус АВ веса Р и невесомый стержень ВС с криволинейной осью произвольного очертания соединены шарнирно в точке В и так же соединены с опорами А и С, расположенными на одной горизонтали АС. Прямые АВ и ВС образуют с прямой АС углы α = 45°. Определить реакции опор А и С.
Ответ: Ra = Р, Rc =√2P/4
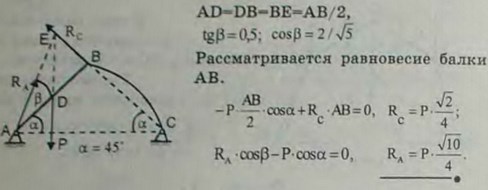
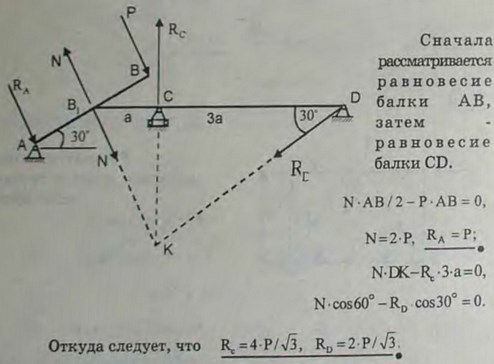
2.42(2.42). Наклонная балка АВ, на конец которой действует сила Р, серединой В1 опирается на ребро консоли балки CD. Определить опорные реакции, пренебрегая весом балок.
Ответ: Ra = Р, RС = 4Р/√3, Rd = 2P/√3.
2.43(2.43). Дана система, состоящая из четырех арок, размеры которых указаны на рисунке. Определить реакции опор А, В, С и D, возникающие при действии горизонтальной силы Р.
Ответ: Ra = P √2/2, Rb = Р, RC = P, RD = P√2/2.

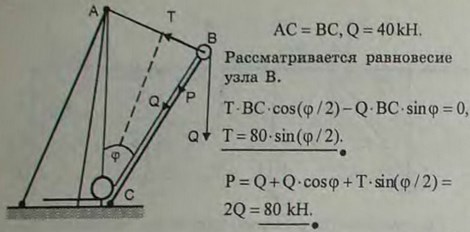
2.44(2.44). Кран состоит из неподвижной башни АС и подвижной фермы ВС, которая имеет шарнир С и удерживается тросом АВ. Груз Q = 40 кН висит на цепи, перекинутой через блок в точке В и идущей к вороту по прямой ВС. Длина АС = ВС. Определить, пренебрегая весом фермы и трением на блоке, натяжение Т троса АВ и силу Р, сжимающую ферму по прямой ВС, как функции угла АСВ = φ.
Ответ: Т = 80 sin(φ/2) кН; Р = 80 кН независимо от угла φ.
2.45(2.45). Блок С с грузом Р = 18 Н может скользить вдоль гибкого троса АСВ, концы которого А и В прикреплены к стенам. Расстояние между стенами 4 м; длина троса 5 м. Определить натяжение троса при равновесии блока с грузом, пренебрегая весом троса и трением блока о трос. Натяжения частей троса АС и СВ одинаковы; их величина может быть определена из подобия треугольника сил и равнобедренного треугольника, одна из боковых сторон которого есть прямая ВСЕ, а основание лежит на вертикали BD.
Ответ: 15 Н независимо от высоты BF.

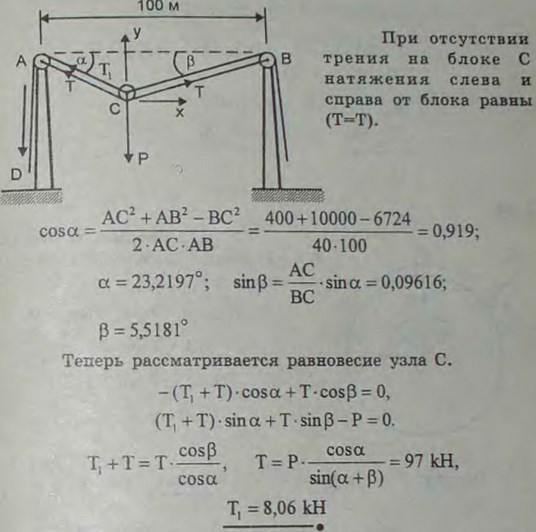
2.46(2.46). Для переправы через реку устроена люлька L, которая посредством ролика С подвешена к стальному тросу AВ, закрепленному в вершинах башен A и В. Для передвижения ролика С к левому берегу служит канат CAD, перекинутый через блок А и наматываемый на ворот D; такой же канат имеется для подтягивания люльки к правому берегу. Точки A и В находятся на одной горизонтали на расстоянии АВ = 100 м одна от другой; длина троса AСВ равна 102 м; вес люльки 50 кН. Пренебрегая весом канатов и троса, а также трением ролика о трос, определить натяжение каната CAD и натяжение троса АСВ в тот момент, когда длина ветви АС = 20 м.
Ответ: SCAD = 8,06 кН; SCB = SCA = 97 кН.
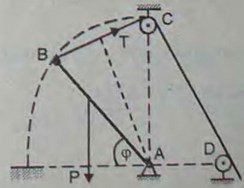
2.47(2.47). Оконная рама AВ, изображенная на рисунке в разрезе, веса 100 Н, открывается, вращаясь вокруг горизонтальной оси A, при помощи шнура BCD, огибающего блоки С и D. Блок С, размерами которого пренебрегаем, и точка А лежат на одной вертикали; вес рамы приложен в ее середине; трением также пренебрегаем. Найти натяжение Т шнура в зависимости от угла φ, образуемого рамой АВ с горизонталью AH, предполагая АВ = AC, а также наибольшее и наименьшее значения этого натяжения.
Ответ: Т = 100 sin (45° - φ/2) Н;
Тmax = 70,7 Н при φ = 0;
Tmin = 0 при ф = 90°.

2.48(2.48). На круглом гладком цилиндре с горизонтальной осью и радиуса ОА =0,1 м лежат два шарика А и В; вес первого 1 Н, второго 2 Н. Шарики соединены нитью АВ длины 0,2 м. Определить углы φ1 и φ2, составляемые радиусами ОА и ОВ с вертикальной прямой ОС в положении равновесия, и давления N1 и N2 шариков на цилиндр в точках А и В. Размерами шариков пренебречь.
Ответ: φ1 = 2 - φ2, tg φ2 = sin2/(2+cos2), φ1 = 84°73', φ2 = 29°86',
N1 = cos φ1 Н = 0,092 Н, N2 = 2 cos φ2 Н = 1,73 Н.

2.49(2.49). Гладкое кольцо Л может скользить без трения по неподвижной проволоке, согнутой по окружности, расположенной в вертикальной плоскости. К кольцу подвешена гиря Р и привязана веревка AВС, которая перекинута через неподвижный блок В, находящийся в высшей точке окружности; размерами блока пренебрегаем. В точке С подвешена гиря Q. Определить центральный угол φ дуги АВ в положении равновесия, пренебрегая весом кольца и трением на блоке, и указать условие, при котором возможно равновесие.
Ответ: sin(φ1/2) = Q/(2P), φ2 = π; первое из указанных положений равновесия возможно при Q < 2Р, второе — при любых Q и Р.

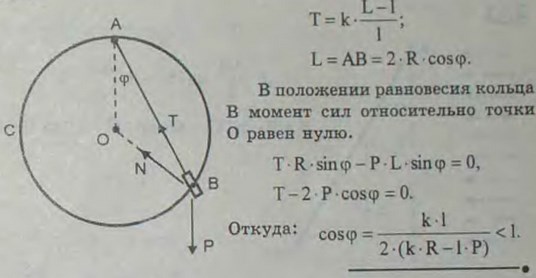
2.50(2.50). На проволочной окружности АВС радиуса R, расположенной в вертикальной плоскости, помещено гладкое кольцо В, вес которого р; размерами кольца пренебречь. Кольцо посредством упругой нити АВ соединено с наивысшей точкой А окружности. Определить угол φ в положении равновесия, зная, что сила натяжения нити Т пропорциональна ее относительному удлинению, причем коэффициент пропорциональности равен k. Если через L и l обозначим длину нити соответственно в состоянии растянутом и нерастянутом, то T = k*((L-l)/l)
Ответ: cosφ = 1/2 kl/(kR-pl, если k ≥ 2pl/(2R-l); в противном случае φ = 0.
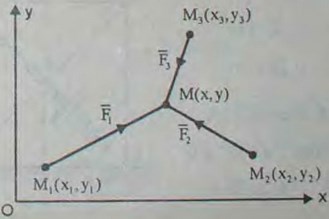
2.51(2.51). Точка М притягивается тремя неподвижными центрами M1(x1, y1), М2(х2, у2) и М3(х3,у3) силами, пропорциональными расстояниям: F1 = k1r1, F2 = k2r2 F3 = k3r3, где r1 = MM1, r2 = ММ2, r3 = ММ3, a k1, k2, k3 — коэффициенты пропорциональности. Определить координаты х, у точки М в положении равновесия.
Ответ: x = (k1x1+k2x2+k3x3)/(k1+k2+k3), y = (k1y1+k2y2+k3y3)/(k1+k2+k3)

2.52(2.52). Однородная прямоугольная пластинка веса 50 Н подвешена так, что может свободно вращаться вокруг горизонтальной оси, проходящей вдоль одной из ее сторон. Равномерно дующий ветер удерживает ее в наклонном положении под углом 18° к вертикальной плоскости. Определить равнодействующую давлений, производимых ветром на пластинку перпендикулярно ее плоскости.
Ответ: 5 sin 18° = 15,5 Н.
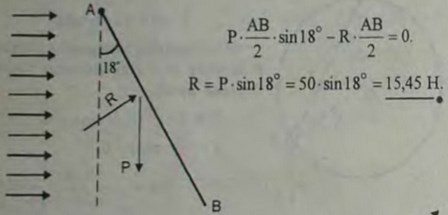
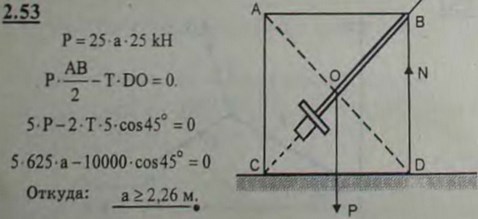
2.53(2.53). Концевая цепь цепного моста заложена в каменное основание, имеющее форму прямоугольного параллелепипеда, среднее сечение которого есть ABDC. Стороны АВ = АС = 5 м, удельный вес кладки 25 кН/м3; цепь расположена на диагонали ВС. Найти необходимую длину а третьей стороны параллелепипеда, если натяжение цепи Т = 1000 кН. Основание должно быть рассчитано на опрокидывание вокруг ребра D; пра расчете пренебрегаем сопротивлением грунта.
Ответ: а > 2,26 м.
2.54(2.54). Земляная насыпь подпирается вертикальной каменной стеной АВ. Найти необходимую толщину стены а, предполагая, что давление земли на стену направлено горизонтально, приложено на 1/3 ее высоты и равно 60 кН/м (на метр длины стены); удельный вес кладки 20 кН/м3. Стена должна быть рассчитана на опрокидывание вокруг ребра А.
Ответ: а ≥ 1,42 м.

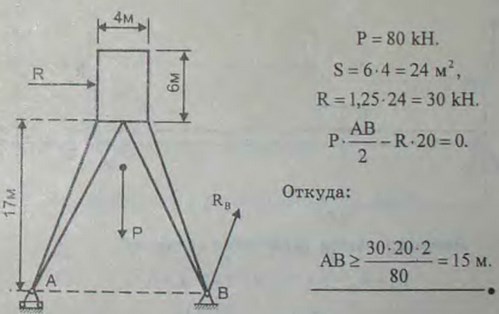
2.55(2.55). Водонапорная башня состоит из цилиндрического резервуара высоты 6 м и диаметра 4 м, укрепленного на четырех симметрично расположенных столбах, наклонных к горизонту; дно резервуара находится на высоте 17 м над уровнем опор; вес башни 80 кН, давление ветра рассчитывается на площадь проекции поверхности резервуара на плоскость, перпендикулярную направлению ветра, причем удельное давление ветра принимается равным 1,25 кПа. Определить необходимое расстояние АВ между основаниями столбов. Расстояние АВ должно быть рассчитано на опрокидывание давлением ветра при горизонтальном его направлении.
Ответ: АВ ≥ 15 м.