3.1. ЭЛЕКТРОСТАТИКА

● Закон Кулона

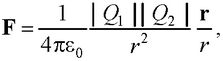
где F – сила взаимодействия двух точечных зарядов Q₁ и Q₂ в вакууме; r – расстояние между зарядами; ε₀ – электрическая постоянная, равная 8,85 ⋅10^–12 Ф/м.

● Напряженность и потенциал электростатического поля

E = F/Q₀; ϕ = П/Q₀ или ϕ = A_∞ /Q₀ ,

где F – сила, действующая на точечный положительный заряд Q₀ , помещенный в данную точку поля; П – потенциальная энергия заряда Q₀ ; A_∞ – работа перемещения заряда из данной точки поля за его пределы.

● Напряженность и потенциал электростатического поля точечного заряда на расстоянии от заряда

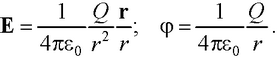
● Поток вектора напряженности через площадку

dΦ_E = EdS = E_ndS ,

где dS = dSn – вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке; E_n – составляющая вектора E по направлению нормали к площадке.

● Поток вектора напряженности через произвольную поверхность S

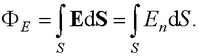
● Принцип суперпозиции (наложения) электростатических полей

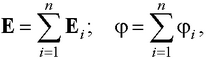
где E_i , ϕ_i – соответственно напряженность и потенциал поля, создаваемого зарядом.

● Связь между напряженностью и потенциалом электростатического поля

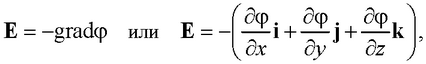
где i, j, k – единичные векторы координатных осей.

● В случае поля, обладающего центральной или осевой симметрией,

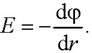
● Электрический момент диполя (дипольный момент)

p = |Q| I,

где I – плечо диполя.

● Линейная, поверхностная и объемная плотности зарядов

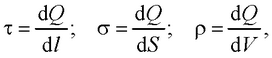
т.е. соответственно заряд, приходящийся на единицу длины, поверхности и объема.

● Теорема Гаусса для электростатического поля в вакууме

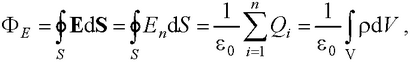
где ε₀ – электрическая постоянная; 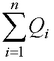 – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности S ; n – число зарядов; ρ – объемная плотность зарядов.

● Напряженность поля, создаваемого равномерно заряженной бесконечной плоскостью

E = σ/(2ε₀).

● Напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями

E = σ/ε₀ .

● Напряженность поля, создаваемого равномерно заряженной сферической поверхностью радиусом R c общим зарядом Q на расстоянии r от центра сферы

E = 0 при r < R (внутри сферы);

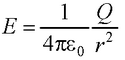 при r ≥ R (вне сферы).

● Напряженность поля, создаваемого объемно заряженным шаром радиусом R с общим зарядом Q на расстоянии r от центра шара

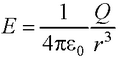 при r ≤ R (внутри шара);

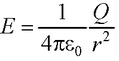 при r ≥ R (вне шара).

● Напряженность поля, создаваемого равномерно заряженным бесконечным цилиндром радиусом R на расстоянии r от оси цилиндра,

E = 0 при r < R (внутри цилиндра);

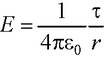 при r ≥ R (вне цилиндра).

● Циркуляция вектора напряженности электростатического поля вдоль замкнутого контура

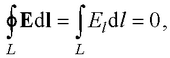
где E_l – проекция вектора Е на направление элементарного перемещения dl. Интегрирование производится по любому замкнутому пути L.

● Работа, совершаемая силами электростатического поля при перемещении заряда Q₀ из точки 1 в точку 2

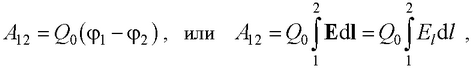
где E_l – проекция вектора Е на направление элементарного перемещения dl.

● Поляризованность

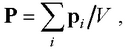
где V – объем диэлектрика; p_i – дипольный момент i-й молекулы.

● Связь между поляризованностью диэлектрика и напряженностью электростатического поля

P = χε₀E ,

где χ – диэлектрическая восприимчивость вещества.

● Связь диэлектрической проницаемости ε с диэлектрической восприимчивостью χ :

ε =1+ χ .

● Связь между напряженностью Е поля в диэлектрике и напряженностью E0 внешнего поля

E = E₀ − P/ε₀ , или E = E₀/ε.

● Связь между векторами электрического смещения и напряженностью электростатического поля

D = ε₀εE .

● Связь между D, E и P

D = ε₀E + P .

● Теорема Гаусса для электростатического поля в диэлектрике

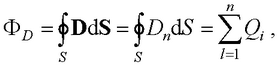
где 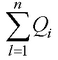 – алгебраическая сумма заключенных внутри замкнутой поверхности S свободных электрических зарядов; D_n – составляющая вектора D по направлению нормали к площадке – вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке. Интегрирование ведется по всей поверхности.

● Напряженность электростатического поля у поверхности проводника

E = σ/(ε₀ε) ,

где σ – поверхностная плотность зарядов.

● Электроемкость уединенного проводника

C = Q/ϕ ,

где Q – заряд, сообщенный проводнику; ϕ – потенциал проводника.

● Емкость плоского конденсатора

C = ε₀εS / d ,

где S – площадь каждой пластины конденсатора; d – расстояние между пластинами.

● Емкость цилиндрического конденсатора

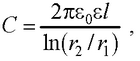
где l – длина обкладок конденсатора; r₁ , r₂ – радиусы полых коаксиальных цилиндров.

● Емкость сферического конденсатора

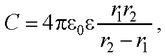
где r₁ и r₂ – радиусы концентрических сфер.

● Емкость системы конденсаторов при последовательном и параллельном соединении

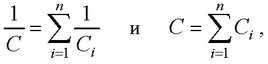
где C_i – емкость i-го конденсатора; n – число конденсаторов.

● Энергия уединенного заряженного проводника

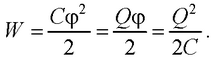
● Энергия взаимодействия системы точечных зарядов

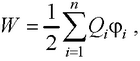
где ϕ_i – потенциал, создаваемый в той точке, где находится заряд Q_i всеми зарядами, кроме i-го.

● Энергия заряженного конденсатора

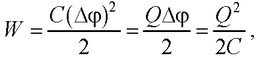
где Q – заряд конденсатора; C – его емкость; Δϕ – разность потенциалов между обкладками.

● Сила притяжения между двумя разноименно заряженными обкладками конденсатора

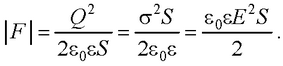
● Энергия электростатического поля плоского конденсатора

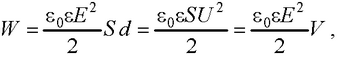
где S – площадь одной пластины; U – разность потенциалов между пластинами; V = Sd – объем конденсатора.

● Объемная плотность энергии

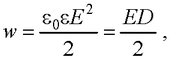
где D – электрическое смещение.

3.2. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

● Сила и плотность электрического тока

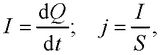
где S – площадь поперечного сечения проводника.

● Плотность тока в проводнике

j = ne 〈v〉 ,

где 〈v〉 – скорость упорядоченного движения зарядов в проводнике; n – концентрация зарядов.

● Электродвижущая сила, действующая в цепи,

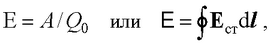
где Q₀ – единичный положительный заряд; A – работа сторонних сил; Ест – напряженность поля сторонних сил.

● Сопротивление R однородного линейного проводника, проводимость G проводника и удельная электрическая проводимость γ вещества проводника

R = ρl / S; G =1/ R; γ =1/ρ,

где ρ – удельное электрическое сопротивление; S – площадь поперечного сечения проводника; l – его длина.

● Сопротивление проводников при последовательном и параллельном соединении

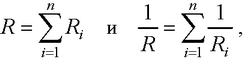
где R_i – сопротивление i-го проводника; n – число проводников.

● Зависимость удельного сопротивления ρ от температуры

ρ = ρ₀ (1+ αt) ,

где α – температурный коэффициент сопротивления.

● Закон Ома:

– для однородного участка цепи

I =U / R ;

– для неоднородного участка цепи

I = (ϕ₁ − ϕ₂ +E₁₂ )/ R ;

– для замкнутой цепи

I = E / R ,

где U – напряжение на участке цепи; R – сопротивление цепи (участка цепи); (ϕ₁ − ϕ₂) – разность потенциалов на концах участка цепи; E₁₂ – э.д.с. источников тока, входящих в участок; E – э.д.с. всех источников тока цепи.

● Закон Ома в дифференциальной форме

j = γE ,

где E – напряженность электростатического поля.

● Работа тока за время t

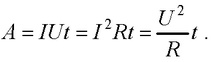
● Мощность тока

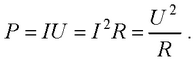
● Закон Джоуля-Ленца

Q = I²Rt = IUt ,

где Q – количество теплоты, выделяющееся в участке цепи за время t .

● Закон Джоуля-Ленца в дифференциальной форме

w = jE = γE² ,

где w – удельная тепловая мощность тока.

● Правило Кирхгофа

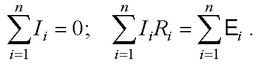
3.3. ЭЛЕКТРИЧЕСКИЕ ТОКИ В МЕТАЛЛАХ,

В ВАКУУМЕ И ГАЗАХ

● Контактная разность потенциалов на границе двух металлов 1 и 2

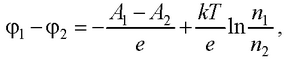
где A₁ , A₂ – работы выходов свободных электронов из металлов; k – постоянная Больцмана; n₁, n₂ – концентрации свободных электронов в металлах.

● Термоэлектродвижущая сила

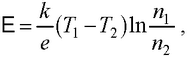
где (T₁ −T₂) – разность температур спаев.

● Формула Ричардсона-Дешмана

j_нас = CT²e^−A/(kT),

где j_нас – плотность тока насыщения термоэлектронной эмиссии; C – постоянная, теоретически одинаковая для всех металлов; A – работа выхода электрона из металла.

3.4. МАГНИТНОЕ ПОЛЕ

● Механический момент, действующий на контур с током, помещенный в однородное магнитное поле,

M = [p_mB] ,

где B – магнитная индукция; p_m – магнитный момент контура с током:

p_m = ISn ,

где S – площадь контура с током; n – единичный вектор нормали к поверхности контура.

● Связь магнитной индукции B и напряженности H магнитного поля

B = μ₀μH ,

где μ₀ – магнитная постоянная; μ – магнитная проницаемость среды.

● Закон Био-Савара-Лапласа

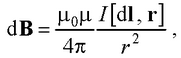
где dB – магнитная индукция поля, создаваемая элементом длины dl проводника с током I ; r – радиус-вектор, проведенный от dl к точке, в которой определяется магнитная индукция.

● Модуль вектора dB

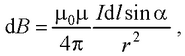
где α – угол между векторами dl и r .

● Принцип суперпозиции (наложения) магнитных полей

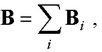
где B – магнитная индукция результирующего поля; B_i – магнитные индукции складываемых полей.

● Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током

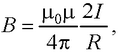
где R – расстояние от оси проводника.

● Магнитная индукция в центре кругового проводника с током

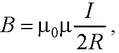
где R – радиус кривизны проводника.

● Закон Ампера

dF = I[dI, B],

где dF – сила, действующая на элемент длины dl проводника с током I , помещенный в магнитное поле с индукцией В.

● Модуль силы Ампера

dF = IBl sinα ,

где α – угол между векторами dl и В.

● Сила взаимодействия двух прямых бесконечных прямолинейных параллельных проводников с токами I1 и I2

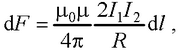
где R – расстояние между проводниками; dl – отрезок проводника.

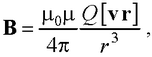
где r – радиус-вектор, проведенный от заряда к точке наблюдения.

● Модуль магнитной индукции

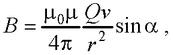
где α – угол между векторами v и r.

● Сила Лоренца

F = Q[vB] ,

где F – сила, действующая на заряд Q, движущийся в магнитном поле со скоростью v.

● Формула Лоренца

F = QE +Q[v, B],

где F – результирующая сила, действующая на движущийся заряд Q, если на него действует электрическое поле напряженностью Е и магнитное поле индукцией В.

● Холловская поперечная разность потенциалов

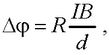
где В – магнитная индукция; I – сила тока; d – толщина пластинки; R =1/(en) – постоянная Холла (n – концентрация электронов).

● Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В)

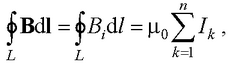
где μ₀ – магнитная постоянная; dl – вектор элементарной длины контура, направленной вдоль обхода контура; B_i = B cosα – составляющая вектора В в направлении касательной контура L произвольной формы (с учетом выбранного направления обхода); угол между векторами В и dl; 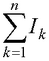 – алгебраическая сумма токов, охватываемых контуром.

● Магнитная индукция поля внутри соленоида (в вакууме), имеющего N витков,

B = μ₀NI / l ,

где l – длина соленоида.

● Магнитная индукция поля внутри тороида (в вакууме)

B = μ₀NI / 2πr .

● Поток вектора магнитной индукции (магнитный поток) через площадку dS

dΦ_B = BdS = B_ndS ,

где dS = dSn – вектор, модуль которого равен dS, а направление совпадает с нормалью n к площадке; B_n – проекция вектора В на направление нормали к площадке.

● Поток вектора магнитной индукции через произвольную поверхность S

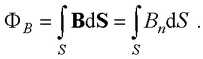
● Потокосцепление (полный магнитный поток, сцепленный со всеми витками соленоида)

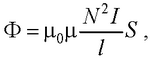
где μ – магнитная проницаемость среды.

● Работа по перемещению проводника с током в магнитном поле

dA = IdΦ ,

где dΦ – магнитный поток, пересеченный движущимся проводником.

● Работа по перемещению замкнутого контура с током в магнитном поле

dA = IdΦ' ,

где dΦ' – изменение магнитного потока, сцепленного с контуром.

3.5. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

● Закон Фарадея

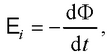
где E_i – э.д.с. индукции.

● Э.д.с. индукции, возникающая в рамке площадью S при вращении рамки с угловой скоростью в однородном магнитном поле с индукцией B ,

E_i = BSω sinωt ,

где ωt – мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.

● Магнитный поток, создаваемый током I в контуре с индуктивностью L,

Φ = LI .

● Э.д.с. самоиндукции

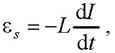
где L – индуктивность контура.

● Индуктивность соленоида (тороида)

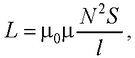
где N – число витков соленоида; l – его длина.

● Токи при размыкании и при замыкании цепи

 I = I₀e^-t/τ; I = I₀ (1 - e^-t/τ),

где τ = L / R – время релаксации (L – индуктивность; R – сопротивление).

● Э.д.с. взаимной индукции (э.д.с., индуцируемая изменением силы тока в соседнем контуре)

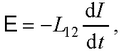
где L₁₂ – взаимная индуктивность контуров.

● Взаимная индуктивность двух катушек (с числом витков N₁ и N₂ , намотанных на общий тороидальный сердечник,

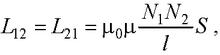
где μ₀ – магнитная проницаемость сердечника; I – длина сердечника по средней линии; S – площадь сердечника.

● Коэффициент трансформации

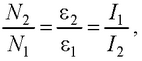
где N, ε, I – соответственно число витков, э.д.с. и сила тока в обмотках трансформатора.

● Энергия магнитного поля, создаваемого током в замкнутом контуре, по которому течет ток I,

W = LI² / 2 .

● Объемная плотность энергии однородного магнитного поля длинного соленоида

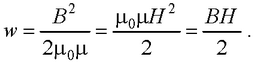
3.6. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА

● Связь орбитального магнитного p_m и орбитального механического L_e моментов электрона

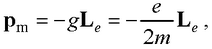
где g = e /(2m) – гиромагнитное отношение орбитальных моментов.

● Намагниченность

J = P_m /V = Σp_a /V ,

где P_m = Σp_a – магнитный момент магнетика, равный векторной сумме магнитных моментов отдельных молекул.

● Связь между намагниченностью и напряженностью магнитного поля

J = χH ,

где χ – магнитная восприимчивость вещества.

● Связь между векторами B, H, J

B = μ₀ (H + J) ,

где μ₀ – магнитная постоянная.

● Связь между магнитной проницаемостью и магнитной восприимчивостью вещества

μ =1+ χ .

● Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В)

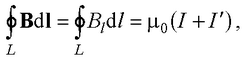
где dl – вектор элементарной длины контура, направленный вдоль обхода контура; B_l – составляющая вектора В в направлении касательной контура L произвольной формы; I и I' – соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых заданным контуром.

● Теорема о циркуляции вектора напряженности магнитного поля

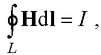
где I – алгебраическая сумма токов проводимости, охватываемых контуром L.

3.7. ОСНОВЫ ТЕОРИИ МАКСВЕЛЛА

ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

● Плотность тока смещения

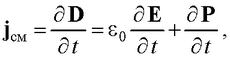
где D – электрическое смещение; 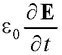 – плотность тока смещения в вакууме;  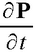– плотность тока поляризации.

● Полная система уравнений Максвелла:

– в интегральной форме

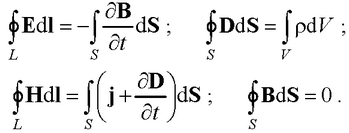
– в дифференциальной форме

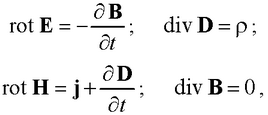
где D = ε₀εE; B = μ₀μH; j = γE (ε₀ и μ₀ – соответственно электрическая и магнитная постоянные; (ε и μ – диэлектрическая и магнитная проницаемости; γ – удельная проводимость вещества).