Эквивалентная схема генератора частоты с взрывомагнитным эффектом
Основной составляющей взрывомагнитного генератора частоты (ВМГЧ) является спиральный магнетокумулятивный генератор, который гальванически связан с малоемкостным конденсатором. Чтобы описать работу данного прибора, применяют понятие (или концепцию) эквивалентной цепи (ЭЦ). При необходимости можно вычислить ток в катушке ВМГЧ и получить хорошее согласование с экспериментальными данными для тока, полученными от пояса Роговского путем опытного подбора параметров эквивалентной цепи ВМГЧ. В связи с этим можно сделать вывод, что концепция ЭЦ достаточно точно описывает поведение электрического тока в приборе. Но модель высокочастотного (ВЧ) излучения, которое генерируется с помощью ВМГЧ, невозможно описать посредством применения концепции ЭЦ. В данной статье проводится анализ эквивалентной цепи прибора, а также допустимых механизмов ВЧ излучения. Затем производится сравнение экспериментальных данных, полученных в тестах, которые были проведены в июне 1997 и августе 1998 гг., с результатами настоящего анализа.
Введение
Далеко не все магнетокумулятивные генераторы способны генерировать высокочастотное радиоизлучение [1]. Этим свойством обладают лишь те магнетокумулятивные генераторы, которые снабжены конденсатором. Благодаря наличию конденсатора становится возможным высокочастотное излучение в полосе от 1 до 150 ГГц системой ВМГЧ (прибор показан на рис.1) [2, 3].

Рис.1 (25 KB).
Авторы статьи [4] описали устройство и работу ВМГЧ и, кроме того, предложили теоретическую модель функционирования ВМГЧ. Эта модель была основана на работе эквивалентной цепи. Экспериментально доказано наличие ВЧ излучения и тока в катушке прибора, по форме напоминающего рыбу (рис.2). Этот последний факт объясняется через исследование ЭЦ прибора, что не объясняет, почему ВМГЧ излучает гармоники выше чем 10 МГц.
Необходимо определить физический механизм ВЧ излучения, особенно гармоник выше 10 МГц. Осцилляции тока в цепи ВМГЧ не превышают 10 МГц (это подтверждается экспериментами), тогда как по данным спектрометров большая часть энергии радиоизлучения находится в полосе частот от 10 до 150 ГГц. Как раз наличие таких высоких частот радиоизлучения и является основной загадкой работы ВМГЧ.

Рис.2.(12 KB)
Обоснованность применения эквивалентной схемы для ВМГЧ
Основными составляющими прибора ВМГЧ являются так называемый лайнер, алюминиевая труба, катушка медного провода и конденсатор. Катушка, намотанная на лайнер, слоем лака изолирована от него, конденсатор присоединён непосредственно одним контактом к лайнеру, а другим – к катушке, алюминиевая труба имеет расширение по диаметру, вызванное взрывом. Конструкция ВМГЧ показана на рис.3. Труба имеет диаметр 40-50 мм, катушка – 1 мм, а конденсатор характеризуется ёмкостью 0.1 - 1 мкФ.
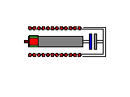
Рис.3. (9 KB)
Теперь рассмотрим обсуждаемый прибор в действии. ВМГЧ работает таким образом: при детонации внутри лайнера взрывчатого вещества одновременно происходит разряд электрическим импульсом внешнего конденсатора большой ёмкости на катушку, т.е. этот конденсатор осуществляет питание катушки. В результате появляется магнитное поле между катушкой и лайнером, которое порождается током в катушке. Во время взрыва происходит расширение лайнера, после чего магнитное поле сжимается, усиливая ток в катушке. Те же самые процессы протекают в обычных магнетокумулятивных генераторах.
Во время контакта края лайнера и крайнего витка катушки происходит замыкание цепи: катушка - конденсатор - лайнер - катушка. При этом происходит механическое разрушение слоя изолятора краем лайнера. Благодаря тому, что электрическая цепь ВМГЧ содержит конденсатор (в отличие от обычных магнетокумулятивных генераторов), в цепи происходят колебания тока. В цепи имеются два тока, один из них (Ij), циркулирующий вокруг лайнера, параллелен току в катушке. Второй (I), течет вдоль лайнера, а затем через конденсатор, в катушке. Поскольку площадь проводящего слоя лайнера в срезе по диаметру намного меньше площади боковой поверхности лайнера, то плотность тока I будет много больше плотности тока Ii. Благодаря этому ток Ii можно не учитывать.
В этой статье мы не рассматриваем координатную зависимость электрических параметров прибора, поэтому мы будем описывать катушку только её индуктивностью L, котораязависит от времени. Обозначим полное сопротивление цепи как R(t) и ёмкость конденсатора как С. При этом ёмкость конденсатора не зависит от времени. Магнитное поле внутри катушки ВМГЧ колеблется с довольно высокой частотой 10 МГц, поэтому процесс усиления тока в данном случае нельзя описать заданием нужной временной зависимости полной индуктивности прибора. Задание временной зависимости индуктивности приведет к тому, что некоторые эффекты, вызванные сжатием магнитного поля, будет невозможно описать. Наилучшим выходом в данной ситуации будет введение в схему определённый генератор напряжения G. Такое решение может иметь место, поскольку изменение магнитного потока вызывает появление ЭДС, а ток является вторичным эффектом. Следовательно, эквивалентную цепь можно описать такой диаграммой:
|----L----C----R ---|
| |
|------G------------|
Уравнение Кирхгофа для ЭЦ будет иметь вид:
![]() (1)
(1)
Здесь Ф определяется как полный магнитный поток, заключённый между лайнером и катушкой, LC(t) – это самоиндукция катушки и IC – ток в катушке. Нужно заметить, что в электродинамике магнитный поток определяется как число силовых линий магнитного поля, которые пересекают некоторый замкнутый контур, следовательно величина Ф соответствует сумме всех магнитных потоков для каждого витка катушки, принимающих участие в процессе сжатия.
Введём связь между магнитным потоком и током в катушке, с учётом того, что в приборе магнитный поток создаётся двумя токами: током в катушке IC и током в лайнере IL, что вызвано эффектом потери диффузионного сопротивления катушки. В соответствии с уравнением Максвелла, при пересечении магнитным потоком витков катушки, в катушке создаётся электрическое поле:
![]() (2)
(2)
Данное электрическое поле создаёт дополнительный ток dI, который не позволяет магнитному полю проникнуть через материал провода катушки. Для обычных магнетокумулятивных генераторов пересечение магнитного потока сквозь внешнюю катушку всегда приводит к увеличению в ней тока. Но есть конденсатор в цепи ВМГЧ, который создаёт собственное электрическое поле в проводе катушки при зарядке его током катушки. Тогда при некотором значении напряжения в проводе пересечение материала провода магнитным потоком уже не будет порождать второстепенный ток dI. Это обусловлено тем, что создаваемое электрическое поле, согласно закону Фарадея, будет скомпенсировано электрическим полем конденсатора. А поскольку приращение тока в проводе отсутствует, то не будет и экранировки проникающего в провод магнитного потока, что влечёт за собой появление бесконечной глубины диффузии магнитного поля и магнитный поток рассеивается из области между катушкой и лайнером, при этом скорость этого рассеивания прямо пропорциональна напряжению на конденсаторе.
Ток IL в лайнере (который совпадает с Ii) удовлетворяет следующему соотношению
![]() ,
,
несмотря на то, что ток IC в катушке равен нулю в определённые моменты времени, и ясно, что нули IL не совпадают с нулями IC . Но лайнер можно приближённо описать как соленоид, для которого если “внешняя сила”, то есть поле внешней катушки исчезает, ток стремится распределиться так, что магнитное поле, создаваемое током IL, концентрируется только внутри соленоида. Поэтому ток IL будет перераспределяться с внешней поверхности лайнера на внутреннюю и поэтому оно будет исключено из дальнейшего процесса сжатия потока.
Следует сказать что достаточно сложно строго описать процесс перераспределения тока IL, поэтому целесообразно использовать для описания этого процесса следующую аппроксимацию:
IL(t) = a IC (t-t )
то есть поведение тока на лайнере повторяет с некоторой временной задержкой поведение тока в катушке (здесь a < 1 и величина параметра t определяется временем проникновения тока IL с внешней поверхности лайнера на внутреннюю). Тогда магнитный поток в области между катушкой и лайнером может быть описан как:
![]() ; (2)
; (2)
где параметр χ зависит только от геометрических размеров лайнера и катушки, и от скорости детонации V таким образом, что магнитный поток должен быть равен нулю в конце процесса работы ВМГЧ. Это отражает тот факт, что большая часть потерь магнитного потока обусловлена краевыми эффектами: когда лайнер входит в контакт с витками катушки, часть магнитного потока, зажатая между соседними витками, выключается из дальнейшего процесса компрессии потока. Например, мы можем принять для χ зависимость, впервые введённую Павловским и Людаевым [6]:
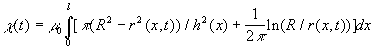
где R – радиус витков катушки, h(x) – шаг витков, r(x,t) – координатная зависимость поверхности лайнера в момент t и l - рабочая длина катушки.
r(x,t) = max[R v (x v Vt)tg(a ) ; r0 ]
где V есть скорость детонации, a угол расширения конуса лайнера и r0 начальный радиус лайнера.
Сделаем следующую аппроксимацию
![]()
принимая во внимание то, что точные вычисления сжатия магнитного потока в форме (2) могут давать ?биение¦ (или удвоение - из-за малой временной задержки t ) частоты, что может приводить к смазыванию чёткой картины осцилляций тока Роговского. Тогда после простых вычислений мы получаем следующее уравнение:
![]() ; (3)
; (3)
где мы учли, что L = LC + c , и опустили малый член d2c /dt2 .
Коэффициент при второй производной не имеет нулей, поэтому согласно теореме Пикара [7] уравнение, как линейное дифференциальное уравнение не имеет особенностей. Следовательно, уравнение (3) подобно уравнению Шрёдингера для волновой функции в квантовой механике и мы вправе распространить методы квантовой механики для анализа этого уравнения. Из экспериментальных данных по измерению тока с помощью пояса Роговского известно, что ток в катушке имеет много осцилляций, поэтому решение для IC должно иметь много (более 50) нулей на рассматриваемом интервале действительной оси переменной t. Известно, что чем больше нулей имеет волновая функция, тем лучше она описывается ВКБ приближением. Соответственно, это же утверждение верно и для ур-ния (3), и ВКБ решение для IC есть:
IC = Ienv * Ioscill
где Ienv огибающая тока и Ioscill безразмерный осциллирующий член. Оба члена выражаются как:
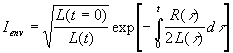 ; (4)
; (4)
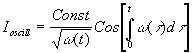 ; (5)
; (5)
где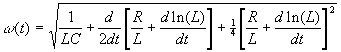 ; (6)
; (6)
Очевидно, что огибающая тока не зависит от ёмкости конденсатора, а только от двух параметров прибора, R и L. Так что мы можем сравнить зависимость (4) с экспериментальными данными, то есть огибающей на осциллограмме тока Роговского. Чтобы получить форму тока ?в виде рыбы¦, мы должны предположить, что индуктивность, а именно, параметр c спадает очень быстро на временах T << toperation и затем выходит на постоянную, пока экспоненциальный член не обрезает полный ток. Формула (4) очень проста и поэтому удобна для анализа экспериментальных данных.
Относительно члена (5) (а также (6)) можно сказать, что несмотря на то, что частота есть функция времени, эта функция вполне аналитичная и не содержит сингулярностей типа ?меандров¦. Эффект появления меандров на диаграмме тока Роговского может быть объяснён удвоением частоты (эффект, вызываемый перераспределинием тока в лайнере), но даже удвоение частоты недостаточно для объяснения появления гегагерцовых гармоник в излучаемом сигнале.
Полезно также отметить один существенный недостаток модели ЭС. Для этого мы проанализируем простейшую электрическую цепь, содержащую лишь конденсатор и катушку (катушка имеет идеальную проводимость). Решение для тока в этой цепи есть:
![]() с
с ![]()
Очевидно, что ток не имеет координатной зависимости, например, по х координате, где х длина провода катушки. Последнее следует из принципа непрерывности тока. Однако, при такой нагрузке антенны (в данном случае антенной является катушка) излучение будет узкополосным, и узко- направленным, и эффективность его будет низка, поскольку волновая длина нагружающего тока много больше геометрических размеров отдельного витка катушки. Аналогично и для ВМГЧ, спектр ЭМ излучения, рассчитанного из выражения для тока без учёта координатной зависимости, должен быть достаточно узким (ни наличие генератора тока, ни учёт сопротивления не меняет принципиально тип колебаний тока v несущая частота остаётся близкой к монохроматической).
Сравнение с экспериментальными данными.
Несмотря на то, что ни рассмотренная выше теоретическая модель, ни результаты других рассмотрений ВМГЧ [1, 3, 4] не объясняют механизма излучения высоких частот, возможно, что существует некоторый неизвестный фактор, обеспечивающий излучение, зарегистрированное во время тестов. Поэтому здесь мы кратко опишем имеющиеся экспериментальные данные
На тесте, проведённом на полигоне Высокогорного геофизического Института в г. Нальчике в 1997 г. были испытаны 4 образца ВМГЧ и в 1998 г. v 10 образцов ВМГЧ. На эти испытания ФБТ ?Сириус¦ поставил одноканальные спектрометры (измеряющие энергию ЭМ импульса в полосе частот 0.5 ГГц и центральными частотами полосы пропускания от 1 до 150 ГГц). Результаты измерений представлены в таблицах 1 и 2:
2.3 GHz | 11.4 GHz | 37.5 GHz | 150 GHz | |
Shot # 1 | 2.5 | 20 | 2.5 | 20 |
Shot # 2 | 0.5 | 10 | 0.5 | 0 |
Shot # 3 | 0.5 | 11.2 | 0.2 | 10 |
Таблица 1. Плотность энергии D(E) [в пикоДж/cм2], измеренная одноканальными спектрометрами ФБТ ?Сириус¦. В верхней строке указаны центральные частоты полос пропускания входных фильтров антенн. Тест 1997 года, радиоизлучение от ВМГЧ. Расстояние между ВМГЧ и датчиками 30 м.
2.3 GHz | 11.4 GHz | 37.5 GHz | 150 GHz | |
Shot # 3 | 1.0 | 4.4 | - | > 25 |
Shot # 4 | 0.5 | 5.3 | 0.5 | 10.8 |
Shot # 5 | 0.5 | - | 0.2 | 2.5 |
Shot # 6 | 0.4 | 29.4 | 0.2 | 2.0 |
Shot # 7 | - | - | 2.5 | |
Shot # 8 | 0.3 | - | - | > 25 |
Shot # 11 | 0.35 | 17.5 | - | > 25 |
Shot # 12 | 0.8 | 4.7 | 0.3 | - |
Таблица 2. Плотность энергии D(E) [в пикоДж/cм2], Тест 1998 года, радиоизлучение от ВМГЧ. Расстояние между ВМГЧ и датчиками 60 м.
При проведении испытаний ВМГЧ спектрометрами измеряются основные параметры ЭМ импульса, излучаемого ВМГЧ, а именно, полная энергия в ЭМ импульсе, пиковая мощность и число колебаний мощности в одном импульсе. В 1997 году проводились тесты, в которых использовались одно- и трехканальные спектрометры, настроенные на несколько частот ниже и выше 10 ГГц. В этих тестах было получено количество осцилляций в сигналах от двух источников ВМГЧ, превосходящее 99. Такое количество осцилляций противоречило тогдашним идеям работы ВМГЧ, поэтому было решено, что это вызвано сбоями в работе измерителей. Однако уровни мощности и энергии в сигналах от ВМГЧ были ниже, чем соответствующие уровни от других источников, поэтому предположения о сбоях в работе спектрометров некорректны.
Исследуя уравнения Кирхгофа для ЭЦ можно сделать вывод, что частота тока в катушке, а следовательно, и излучения, которое является производной от тока, не может достигать частоты, близкой к гигагерцам, даже при возникновении эффекта удвоения частоты. Многие авторы считают, что ВМГЧ создавал бы гегагерцовые гармоники в ЭМ поле, если бы имел место электрический пробой между катушкой и лайнером или между соседними витками катушки. Однако вычисление напряжения между двумя соседними витками катушки, или между лайнером и крайним витком катушки (для которого слой изолятора наиболее разрушен) показывает, что значение этого напряжения много ниже порогового напряжения пробоя. Следовательно, напряжение, создаваемое конденсатором не может явиться источником возникновения пробоя.
Для объяснения возможного появления электрического пробоя и соответственно, высокочастотного ЭМ излучения важно исследовать экспериментальные данные по этому вопросу.
В тесте 1997 года кроме одноканальных спектрометров, регистрирующих сигнал в полосе частот выше 10 ГГц (кроме одного, настроенного на частоту 2.3 ГГц), использовались трёхканальные спектрометы, регистрирующие сигнал при значении частоты 1.4, 2.8, 5.6 и 9.4 ГГц, и измеряющие не только полную энергию в ЭМ импульсе, но и пиковую мощность, а также и число осцилляций мощности в одном импульсе (посылке). Поскольку полный импульс, излучаемый ВМГЧ, имеет очень сложную временную зависимость, современной измерительной базой удаётся измерить лишь некоторые параметры импульса.
В частности, была поставлена задача измерения количества осцилляций мощности в сигнале. При испытаниях различных источников было обнаружено, что в сигналах от двух источников, от ВМГЧ и другого, имеющего сходную конструкцию, количество осцилляций мощности более чем 50 (для большого количества испытаний часть данных имела значение 99, но так как шкала спектрометров была ограничена значением 99, то точное значение количества осцилляций мощности неизвестно; можно лишь сказать, что это значение превосходит 99). Следует отметить, что такие данные по количеству осцилляций мощности в сигнале противоречили существующим концепциям функционирования ВМГЧ, поэтому эти данные не были опубликованы и содержатся лишь в тестовых отчётах (они были интерпретированы как результаты сбоев в работе спектрометров после воздействия на них сигнала от источника; однако, необходимо указать, что уровни мощности и энергии в сигналах от ВМГЧ были ниже, чем соответствующие уровни от других источников, поэтому предположения о сбоях в работе спектрометров некорректны).
Однако, такое количество осцилляций мощности в сигнале может быть объяснено ЭМ излучением от электрического пробоя, возникающим между поверхностью лайнера и ближайшим к поверхности неразрушенным витком катушки (но ещё не имеющим прямого гальванического контакта в лайнером, хотя этот виток соединён гальванически с лайнером через соседние витки).
Электрически пробой, если он есть, должен быть вызван каким-то электрическим полем, и здесь мы укажем возможную причину возникновения такого поля, которая не зависит напрямую от напряжения на конденсаторе. Впервые это было высказано Лоренцем в его парадоксе теории Эйнштейна. Лоренц показал, что ток в прямом бесконечно длинном проводе вызывает электрическое поле, направленное перпендикулярно проводу, и это нарушает принцип эквивалентности систем отсчёта. В данной статье мы не будем анализировать этот парадокс, однако, укажем, что были проведены эксперименты по обнаружению такого тока (хороший обзор и экспериментальные данные содержатся в работе [8], недавние результаты по этому вопросу даны в [9]). Причина появления такого электрического поля достаточно прозрачна: эффект вызван разностью между кулоновским полем неподвижных ионов и полем Льенарда-Вихерта движущихся электронов проводимости. Однако, для корректной экспериментальной проверки эффекта требуется выполнение следующих условий:
- электронейтральность и замкнутость цепи, то есть цепь не должна быть подсоединена к внешнему источнику питания. В противном случае, заряды от источника могут пройти в цепь и нарушить распределение электронной плотности, создаваемой квазистационарным током [9].
- поддержание в течение достаточно долгого времени (достаточного для измерений) квазистационарного тока в цепи;
Поэтому опыты по проверке эффекта возможны лишь для колец со сверхпроводящим током, а для таких объектов возможный эффект очень мал. В то же время оба условия выполняются в ВМГЧ. Поэтому появление Лоренцева электрического поля и, соответственно, пробой возможны в этой системе, особенно, когда изолирующий слой проводов катушки находится в предразрушаемом состоянии и ток в катушке проходит точку экстремума.
Тут может быть задан вопрос: почему такой механизм излучения не реализуется в обычных магнетокумулятивных генераторах (МКГ)? Известно, что в многосекционных МКГ ток может достигать значений до 0.5 МА и представляется, что в таких МКГ условия для возникновения пробоя лучше. Однако, отметим, что в обычных МКГ ток нарастает достаточно медленно в сравнении с ВМГЧ, при этом нарастание тока монотонное. Поэтому если такой пробой происходит, то он единичный и на фоне пробоев в МКГ (известно, что от некоторых МКГ наблюдается слабое рентгеновское излучение, которое также может быть вызвано ускорением электронов мощным электрическим полем) не заметен. В то же время, условия для пробоя в ВМГЧ могут создаваться столько раз, сколько раз ток в катушке прибора проходит точки максимумов и минимумов, то есть не менее 100 раз. Далее, при вычислении разности кулоновских и льенард-вихертовых полей обычно рассматриваются равномерно движущиеся (на фоне ионов) электроны. Однако, в ВМГЧ электроны колеблются с частотой порядка 10 МГц , то есть ускоряются. Следует ожидать, что член с ускорением вносит определённый вклад в разность кулоновских и льенард-вихертовых полей и условия для пробоя в ВМГЧ более благоприятны, чем для МКГ, в которых ток квазистационарный.
Укажем, что описанный выше механизм пробоя может рассматриваться лишь как гипотеза, и необходима экспериментальная проверка этой идеи.
Заключение
В заключение необходимо отметить, что модель ЭС не способна объяснить функционирование прибора. Это следует из тех соображений, что наивысшая частота тока нагрузки для катушки как антенны, не может быть существенно выше 10 МГц (как следует из вычислений, основанных на модели ЭС). В то же самое время частота зарегистрированного в тестовых испытаниях радиоизлучения лежит в полосе от 10
до 150 ГГц. Из всего вышесказанного мы вынуждены заключить, что модель ЭС не способна объяснить функционирование прибора. Отметим, что развитая выше модель ЭС имеет следующие недостатки:
- Для частот выше 100 МГц катушка уже не может быть представлена как идеальный соленоид. Более строгое описание требует рассмотрения катушки (как основного узла прибора) как системы с распределёнными параметрами.
- При переходе от описания реального прибора к ЭС мы внесли упрощения в описание процесса сжатия магнитного поля. Эффекты, утерянные в ходе такого упрощения, могут быть существенны.
Тем не менее, модель ЭС, даже с учётом двух вышеуказанных пунктов, не способна будет объяснить наличия излучения в полосе от 10 до 150 ГГц, и для корректного объяснения требуется какой-то принципиально иной подход.
Несмотря на то, что модель ЭС не способна описать наличие гегагерцового излучения, генерируемого ВМГЧ, эта модель позволяет описать два новых эффекта, ранее не описанных в научной литературе:
- Эта система электрически нейтральна, изолирована от внешних источников тока и в то же время в ней поддерживается квазистационарный (по сравнению с эффектами распространения ЭМ полей) ток. Таким образом, в этой системе реализуются на макроскопическом уровне условия для проверки предположения Лоренца о существовании электрического поля, нарушающего эквивалентность систем отсчёта в специальной теории относительности.
- Эффект проникновения магнитного поля сквозь катушку. Для частоты магнитного поля внутри катушки порядка 10 МГц и для геометрических размеров катушки медного провода глубина скин-слоя должна быть не более 0.1 мм, в то время, как толщина слоя металла в катушке в 10 раз больше. То есть, процесс проникновения магнитного поля через катушку не может быть описан в рамках концепции скин-слоя.
Список литературы
- Prishchepenko A.B., V.K.. Kiseljov, and L.S. Kudimov., Radio Frequency Weapon at the Future BattleField, Proceedings of the EUROEM Conference, Bordeaux, France, June 1994.,
- L. Altgilbers et al., Compact explosive driven sources of microwaves: test results, Proceedings of the Megagauss VIII Conference, Talahassee, USA, October, 1998
- V.A.Soshenko and V.C.Ivanov, Investigation of the Parameters of Explosive Driven Magnetic Generators of Frequency, Proceedings of EUROEMConference, Jerusalem, Izrael, August 1998.
- Прищепенко А.Б., Щелкачёв М.В. Диссипативные и диффузионные потери в спиральном взрывомагнитном генераторе. Электричество, 9, стр. 31-36, 1993.
- Кнопфель, Сверхсильные магнитные поля, М. Мир, 1968. Гл. 4.
- Павловский А.И., Людаев Р.З. и др., Многосекционный генератор МК-2, Материалы конференции Мегагаусс III, М. Наука, 1984, стр. 312-320.
- Джеффри Г., Свирлс Б. Методы математической физики, М. ?Мир¦, 1970. Гл 16.
- W.F. Edwards, C.S. Kenyon, and D.K. Lemon, Continuing investigation into possible electric fields arising from steady conduction currents, Physical Review D, Vol. 14, No. 4, pp. 922-938, 1976.
- L. Baroni, E. Montanari, and A.D. Pesci, Some remarks on the question of charge densities in stationary current-carrying conductors Nuovo Cimento B109, p. 1275, 1994.

