г. Ижевск

Бреган Андрейгр.18-31 1998 год.

Цель работы: определение продольной магнитострикции никеля в зависимости от амплитуды напряженности магнитного поля.

Данная работа посвящена изучению поведедения ферромагнетиков в магнитном поле.

Хотя магнитное взаимодействие является малой поправкой к электрическим обменным силам, обусловливающим самопроизвольную намагниченность, тем не менее, они играют решающую роль во всем сложном комплексе явлений технического намагничивания. Поэтому выяснение физической природы магнитного взаимодействия в ферромагнетиках имеет не только теоретическое значение, но необходимо и для ясного понимания механизма тех физических процессов, которые обусловливают всю практическую ценность явления ферромагнетизма.

Напомним, что ферромагнетиками называются вещества, в которых магнитные моменты ориентированы вдоль выделенного направления.

Монокристаллы ферромагнетиков анизотропны в магнитном отношении. В качестве примера магнитокристаллической анизотропии на рис.1 приведены кривые намагничивания I(Н) монокристалла кобальта, снятые вдоль гексагональной оси (ось с) и перпендикулярно к ней (ось а). Как видно из рисунка, если магнитноеполе H || c, то достаточно приложить поле в несколько сот эрстед для того, чтобы намагнитить кристалл до насыщения. При Н^с насыщение достигается только при Н» 10⁴ Э.

Наиболее резко магнитная анизотропия, проявляется в кристаллах гексагональной симметрии (Со,Tb,Dy). Из анализа кривых I(Н), снятых по различным кристаллографическим направлениям, следует, что в ферромагнитных монокристаллах существуют направления, называемые “осями легкого намагничивания” (ОЛН), и направления, называемые “осями трудного намагничивания” (ОТН).

Известно, что минимум свободной энергии магнитокристаллической анизотропии достигается, когда намагниченность ориентирована вдоль ОЛН. Для поворотаI_s из этих направлений требуется затратаопределенной работы, которая приводит к ростуэнергии магнитной или магнитокристаллической анизотропии.Энергией магнитокристаллической анизотропии называют ту часть энергии кристалла, которая зависит от ориентации вектора намагниченности относительно кристаллографических осей.

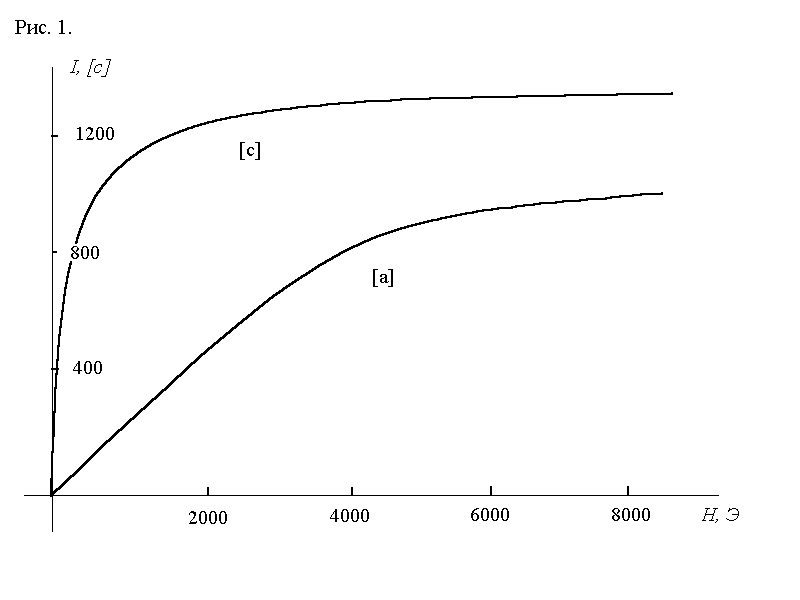
Рис.1. Кривые намагничивания I(Н) монокристалла кобальта, снятые

вдоль гексагональной оси (ось с) и перпендикулярно к ней (ось а).

В случае кобальта эта энергия минимальна, если намагниченность направлена вдоль оси с (при комнатной температуре). При вращении намагниченностиI_s от оси с энергия анизотропии увеличивается с увеличением углаJ между осью c и направлениемI_s, достигает максимума при J=90°, т. е. приI_{s ^}с, и затем уменьшается до первоначального значения при J =180°.

При возможных изменениях ориентации самопроизвольной намагниченности в кристалле изменяются равновесные расстояния между узлами
решетки. Поэтому возникают самопроизвольные магнитострикционные
деформации. т.е.

Опр. При перемагничивании ферромагнетика имеет место магнитное взаимодействие элекектронов, которое влияет на межатомное расстояние, вызывая деформацию кристаллической решетки, что сопровождается изменением линейных размеров тела и появлением соответствующей магнитоупругой энергии. Это явление называется магнитострикцией.

В частном случае кубического кристалла в отсутствие внешних напряжений свободная энергия магнитного и упругого взаимодействия (с точностью до шестых степеней в направляющих косинусах вектораIs и вторых степеней тензора магнитострикционных напряжений), равна сумме энергии магнитокристаллической анизотропии f_a, упругой энергииf_упр и магнитоупругой энергии f_му:

f_a(a_i ,e_{i j})= f_a(a_i ,e_{i j})+ f_упр.(a_i ,e_{i j})+ f_му. (a_i ,e_{i j}) (1)

1) Можно феноменологическим путем получить выражение плотностиf_a энергии магнитной анизотропии, раскладывая эту энергию в ряд по степеням направляющих косинусов вектора намагниченностиa_i относительно осей симметрии кристалла. Сначаланайдем выражениеf_a для кобальта, имеющего гексагональнуюрешетку с ОЛН - с, для которого a_i =a = cos (I_s,с)= cos J. Длягексагональной решетки, обладающей центром симметрии, операция замены a на - a должна оставлять энергию инвариантнойотносительно такого преобразования симметрии. Следовательно,в разложении останутся только члены с четными степенями а,т. е.

f_a=K_1¢a2 + K_2¢a4 + ...... (2)

гдеK_1¢a2и K_2¢a4и т. д. - параметры магнитной анизотропии;f_a чащезаписывают в следующем виде:

f_a =K₁sin^2J+ K₂sin^4J+..., (3)

гдеK₁ и K₂ называют 1-й и 2-й константами магнитной анизотропии.Энергия анизотропии кристаллов гексагональной системы вобщем случае должна зависеть от азимута j. Ноэта зависимость является очень слабой, и ею обычно пренебрегают.Для кубических кристаллов, таких какFe,Ni, энергия анизотропии выражается в функции направляющих косинусов(a₁, a₂, a₃) намагниченностиI_s относительно трех ребер куба:

(a₁=cos(I_s, [100]);a₂=cos(I_s, [010]);a₃=соs(I_s, [001]).(4)

Энергия анизотропии должна быть такой функциейa₁ , a₂ ,_a3,которая оставалась бы инвариантной при преобразованиях симметрии кубического кристалла.

В кубическом кристалле плоскости типа [100] являются плоскостями симметрии. Зеркальное отражение вектораI_s в такойплоскости должно оставлять функциюf_a(a₁,a₂, a₃) инвариантной. Отражение, например, в плоскости (100) заменяетa₁ на- a₁,оставляяa₂ и a₃ неизменными. Аналогично зеркальное отражение в плоскостях (010) и (001) изменяет знаки соответственно уa₂ и a₃. Следовательно, функцияf_a(a₁,a₂,a₃) должна быть инвариантной относительно преобразований

a_i® - a_i (i = 1,2,3) (5)

Кубический кристалл имеет также плоскости симметрии типа {110}. Отражение в этих плоскостях соответствует преобразованиям

a_i® - a_j (i¹ j = 1,2,3) (6)

Первым членом разложения энергии анизотропии кубическогокристалла по степенямa₁ , a₂ , a₃,удовлетворяющим требованиямсимметрии (5,6), являетсяa²₁ + a²₂ + a²₃ , но этот член разложения всегда равен единице и, следовательно, не описывает эффектаанизотропии.
Следующий член (четвертого порядка относительно a_i),a⁴₁ + a⁴₂ + a⁴₃может быть приведен к виду

a⁴₁ + a⁴₂ + a⁴₃ = 1- 2(a²_1a²₂+a²_2a²₃+a²_1a²₃) (7)

так как (a²₁ + a²₂ + a²₃)² = 1. Далее, член шестого порядка приводится к виду

a⁶₁ + a⁶₂ + a⁶₃ = 1- 3(a²_1a²₂+a²_2a²₃+a²_1a²₃)+3a²_1a²_2a²₃(8)

так как (a²₁ + a²₂ + a²₃)³ = 1.

Энергия анизотропии на единицу объема кубического кристалла с точностью до членов шестого порядка относительно a_i представляется в виде линейной комбинации

f_a=K₁(a²_1a²₂+a²_2a²₃+a²_1a²₃)+K_2a²_1a²_2a²₃ (9)

Часто членом K_2a²_1a²_2a²₃, который обычно меньше первого члена в (9), пренебрегают. Тогда:

f_a=K₁(a²_1a²₂+a²_2a²₃+a²_1a²₃) (10)

Знаки константанизотропииK₁ и K₂ и их относительная величина определяютто кристаллографическое направление, которое в данном кристалле будет “легким”.

Если К₁>0, то первый член в (9) минимален при направлении намагниченности вдоль осей [100], [010], [001], которые в этом
случае являются осями легкого намагничивания.
ЕслиК₁<0, то осями легкого намагничивания являются оси[111], [I11],[1I1], [11I], так как первый член в энергии анизотропии (9) минимален, когда намагниченность расположена вдольэтих осей.

Если учитывать и второй член в (9), то направление диагональной оси[100] в тех случаях, когда К₁ отрицательна и меньше по абсолютной величине, чемК₂, также может быть направлением легкого намагничивания.

В заключение отметим, что в ряде случаев удобнееf_a раскладывать в ряд по сферическим функциямY^m_l(J,j) где J - полярный угол, j -азимут вектора намагниченности по отношению к выбранной оси симметрии. Тогда

f_a=SSc^m_lU^m_l(J,j) , (11)

гдеc^m_l - параметры, аналогичные константам анизотропии. Разложение (11) справедливо длякристаллов любой симметрии (тип симметрии определяют величиныc^m_l, т. е. какие из этих коэффициентов обращаются в нуль).

2) f_упр.(e_{i j} ) = ½ [C₁₁(e²_xx+ e²_yy+ e²_zz)] +½ [C₄₄(e²_xy+ e²_yz+ e²_xz)]+

+ C₁₂(e_xxe_yy+ e_yye_zz+ e_xxe_zz ) (12)

3)f_му.(a_i ,e_{i j} ) = B₁[(a²₁ – 1/3)e_xx+(a²₂ – 1/3)e_yy+(a²₃ – 1/3)e_zz]+

B₂[a_1a2e_xy+a_2a3 e_yz+a_1a3e_xz] , (13)

где, a_i – направляющие косинусы вектора спонтанной намагниченности,e_{i j}- компоненты тензора деформации кристалла, В₁ , В₂ – константы магнитоупругой энергии, С₁₁ , С₄₄ , С₁₄ – модули упругости.

Устойчивому равновесному состоянию деформированного кристалла с определенным направлением намагниченности (a_i = const) соответствует минимум свободной энергии. Чтобы определитькомпоненты тензора деформации при отсутствии внешних напряжений, характеризующие спонтанную магнитострикционную деформацию или спонтаннуюмагнитострикцию, следует найти компонентыe⁽⁰⁾_{i j} , соответствующие минимумуf.

Минимизируя выражения для плотности энергииf относительноe _{i j}, получим

∂f/∂e_yy= B₁(a²₂ – 1/3)+C₁₁e⁽⁰⁾_yy + C₁₂(e⁽⁰⁾_zz+e⁽⁰⁾_xx)=0 , (14)

∂f/∂e_yz= B_2a2a3+ C₄₄e⁽⁰⁾_yz=0, (15)

Складывая три уравнения (14), найдем: (∆V/V)₀=e⁽⁰⁾_xx+ e⁽⁰⁾_yy+ e⁽⁰⁾_zz ,

т.е. в этом приближении изменение объема кристалла (∆V/V)₀ при спонтанной магнитострикционной деформации равно нулю. Из (14) и (15) получим компоненты тензора этой деформации

e⁽⁰⁾_{i i} = -[B₁/(C₁₁-C₁₂)] [a²_i – 1/3], e⁽⁰⁾_{i j} = -(B₂/C₄₄)a_iaj ; i , j = x, y, z.

(16)

Знаяe⁽⁰⁾_{i j} легко найти удлинение кристаллаδl/l при спонтанной магнитострикционной деформации в любом направлении, определяемом направляющими косинусамиβ₁, β₂, β₃:

(δl/l)₀ = e⁽⁰⁾_xx β²₁+ e⁽⁰⁾_yy β²₂+ e⁽⁰⁾_zz β²₃+ e⁽⁰⁾_xy β₁ β₂+ e⁽⁰⁾_yz β₂ β₃+ e⁽⁰⁾_zx β₃β₁=

= - [B₁/(C₁₁-C₁₂)] [a²₁ β²₁+a²₂ β²₂+a²₃ β²₃- 1/3] –

– (B₂/C₄₄)(a_1a2 β₁ β₂+a_2a3 β₂ β₃+a_3a1 β₃ β₁) (17)

Найдем δl/lдля кристаллографических направлений [100] и [III].Если кристалл намагничен вдоль направления [100], то, полагаяв (17)

a₁ = β₁ = 1,a₂ = a₃ = β₂ = β₃ = 0, получим

(δl/l)_[100] =λ₁₀₀ = - 2/3 [B₁/(C₁₁-C₁₂)]. (18)

Аналогично для направления [111] будем иметь

(δl/l)_[111] =λ₁₁₁ = - 1/3 (B₂/C₄₄) , (19)

где λ₁₀₀ иλ₁₁₁ носят название констант магнитострикции. Подставляя
в (18,19),Выражения для констант магнитоупругой энергии:

B₁=N(∂g₁/∂r)r₀ , B₂= 2Ng₁, (20)

где - N число атомов в единице объема. Можно выразить магнитострикционные
константыλ₁₀₀ иλ₁₁₁ для различных типов кубических решеток через коэффициентыg₁ в выражении для энергии пары атомов:

1. простая кубическая:

λ₁₀₀ = -2/3[N/(C₁₁ – C₁₂)][∂g₁/∂r]r₀ ;

λ₁₁₁ = - 4/3(N/C₄₄)g₁

2- объемно- центрированная:

λ₁₀₀ = -16/9[N/(C₁₁ – C₁₂)]g₁ ; (21)

λ₁₁₁ = - 16/27[g₁+(∂g₁/∂r)r₀]

3 – гранецентрированная:

λ₁₀₀ = -1/3[N/(C₁₁ – C₁₂)][6g₁ – (∂g₁/∂r)r₀] ;

λ₁₁₁ = - 2/3[N/C₄₄] [2g₁+(∂g₁/∂r) r₀]

Принимая во внимание (16),магнитоупругую (13) и упругую (12) энергии при спонтанной деформации можно записать в виде:

f⁽⁰⁾_му.= [B²₁/(C₁₁ – C₁₂)] ∑ (a²_i-1/3)² - B²₂/C₄₄ ∑ a²_ia²_j , (i , j=1,2,3)

f⁽⁰⁾_упр.= ½ C₁₁ [B²₁/(C₁₁ – C₁₂)²] ∑ (a²_i-1/3)²+ ½ C₄₄ B²₂∑ a²_ia²_j+

+C₁₂[B²₁/(C₁₁ – C₁₂)²] ∑ (a²_i-1/3)(a²_j-1/3), (i , j=1,2,3)

или, учитывая соотношения

1) ∑a² _i =1 (i =1,2,3) ;

2) ∑a⁴ _i =1 –2 ∑a² _{i a}²_j (i , j=1,2,3) ;

3) ∑ (a²_i-1/3)²= 2/3 – 2 ∑ a²_ia²_j (i , j=1,2,3, i>j) ;

4) ∑ (a²_i-1/3)(a²_j-1/3) = ∑ a²_ia²_j – 1/3 (i , j=1,2,3, i>j) ;

f⁽⁰⁾_му.= – [B²₁/(C₁₁ – C₁₂)][ 2/3 – 2 ∑ a²_ia²_j] - B²₂/C₄₄ ∑ a²_ia²_j ,

(i , j=1,2,3, i>j) (22)

f⁽⁰⁾_упр.= ½ C₁₁ [B²₁/(C₁₁ – C₁₂)²] [ 2/3 – 2 ∑ a²_ia²_j]+ ½ C₄₄ B²₂∑ a²_ia²_j+

+C₁₂[B²₁/(C₁₁ – C₁₂)²] ∑ a²_ia²_j – 1/3 ,

(i , j=1,2,3,i>j) (23)

Подставляя (21) и (23) в (1) и учитывая (10), (18) и (19), получим следующее выражение для плотности анизотропной части магнитной энергии кристалла при отсутствии упругих внешних напряжений:

f =(K₁+∆K₁)∑ a²_ia²_j (i , j=1,2,3, i>j) (24)

где добавка ∆K₁ к первой константе анизотропии, обусловленная спонтанной магнитострикционной деформацией равна

∆K₁= [2B²₁/(C₁₁ – C₁₂)] + [B²₂/C₄₄] – [C₁₁{B²₁/(C₁₁ – C₁₂)²}]+

+ [½ C₄₄ (B²₂/C²₄₄)]+[ C₁₂ {B²₁/(C₁₁ – C₁₂)²] =

= [B²₁/(C₁₁ – C₁₂)] – ½[B²₂/C₄₄]=9/4 l²₁₀₀(C₁₁-C₁₂) – 9/2l²₁₁₁C₄₄

(25)

Как видно из (24), вид зависимости плотности энергии от направляющих косинусов не изменился, но константа анизотропии благодаря спонтанной деформации решетки увеличилась.

§2. Физическая природа естественной магнитной анизотропии.

В первых работах Акулова магнитное взаимодействие в ферромагнитных кристаллах с микроскопической точки зрения трактовалось чисто классическим путем. Квантовомеханическая трактовка была дана в работах Блоха и Джентиля. Классическую теорию температурной зависимости констант магнитной анизотропии развили Акулов и Зинер, исходя из представления о том, что около каждого узла решетки можно выделить области ближнего магнитного
порядка с не зависящими от температуры локальными константами анизотропии. Локальные мгновенные намагниченности этих областей из-за теплового движения распределены хаотически и образуют среднюю намагниченность всего кристалла. Отсюда удается определить связь между температурным ходом констант анизотропии и намагниченности в виде

K_n(T)/K_n(0) = [I_s (T)/I_s (0)]^n(2n+1) , (26)

гдеn – порядок константы. Таким образом, мы приходимкуниверсальной зависимости K₁≈ I³_s и K₂≈ I¹⁰_s. Pезультат (26) получается в приближении теории молекулярного поля . Микроскопические трактовки этой проблемы даны в работах Ван - флека и Канамори.

В основе всех расчетов по микроскопической теории магнитной анизотропии лежит учет магнитного взаимодействия между спиновыми
и орбитальными магнитными моментами электронов, принимающих участие в ферромагнетизме. В общем случае оператор магнитной энергиискладывается из трех членов.

H_магн.=U₁+U₂+U₃ (27)

гдеU₁ — оператор, соответствующий движению электронов относительноионов решетки,— спин-орбитальная энергия;U₂ — оператор магнитнойэнергии, возникающей вследствие относительного движения самих электронов, —орбитальная энергия;U₃ — оператор энергии магнитноговзаимодействия спиновых магнитных моментов электронов —спиноваяэнергия (в первом приближении имеет вид дипольного взаимодействия).

Эффект орбитального взаимодействияU₁ иU₂ проявляющийся в случае изолированных атомов в образовании тонкой структуры спектральныхлиний приводит к появлению “внутренних магнитных полей” порядка 10⁵э. С другой стороны, “эквивалентное магнитное поле” анизотропии ферромагнетиков, определяемое величиной поля, при котором достигаетсянасыщение в монокристалле вдоль труднейших направлений намагничивания, оказывается порядка 10²э и лишь в редких случаях(Со, пирротин) достигает 10³—10⁴э. Объяснение этого несоответствия заключается в том, что в отличие от атомов, где орбитальные моменты отличныот нуля (за исключением s-состоянии), в ферромагнитных кристаллах(например, в d-металлах и сплавах), как показывают измерения гиромагнитного эффекта, средний орбитальный магнитный момент по кристаллу почти всегда практически равен нулю. Поэтому в первом приближении эффект спин-орбитальных энергий U₁ иU₂также равен нулю. Отличный от нуля эффект получается лишь во втором и более высоких приближениях.

Что же касается спиновой части магнитного взаимодействияU₃, которая хотя и дает отличный от нуля эффект в первом приближении, но темне менее не обеспечивает наблюдаемый на опыте порядок величины эффективных “полей” благодаря своей малости.

Несмотря на отсутствие законченной квантовой трактовки магнитного
взаимодействия в ферромагнетиках, в этой области имеются известные
успехи. Так, например, удалось объяснить правильный порядок величины констант магнитной анизотропии. В частности, без всяких дополнительных соображений из теории следует, что в кубических кристаллах (Fe,Ni) константы анизотропии должны быть меньше по абсолютнойвеличине, чем в случае гексагональных кристаллов (Со, пирротин). Этовытекает из свойств симметрии кубических кристаллов, в которых первоеприближение для дипольной энергииU₃ и второе приближение для орбитальных энергийU₁ иU₂не приводит к зависимости свободной энергиикристалла от ориентации его намагниченности относительно кристаллографических осей. Для получения этой зависимости надо рассматриватьследующие приближения, в то время как в гексагональных решетках анизотропия получается и в первом приближении дляU₃, и во второмдляU₁ иU₂.

Остановимся несколько подробнее на микромеханизме явления естественной кристаллографической магнитной анизотропии. Поскольку
в создании самопроизвольной намагниченности ферро- и антиферромагнетиков основную роль играют электронные спины, то микроскопическаяэнергия, ответственная за магнитную анизотропию, должна зависеть отсостояния этих спинов в кристалле, а также отражать симметрию распределения спиновой и зарядовой (орбитальной) плотности в кристалле. Наиболее простым является механизм магнитного дипольного взаимодействия спинов.

К сожалению, однако, учет лишь дипольного межэлектронного взаимодействия не может, как правило, объяснить наблюдаемую на опытевеличину энергии магнитной анизотропии.

Другой из упомянутых выше механизмов заключается в связи между
спином и орбитальным движением электронов [например, описываемой
членамиU₁ иU₂ гамильтониана (27)].

Киттель дает следующее наглядное объяснение физического механизма магнитной анизотропии из-за спин-орбитальной связи.
В основу своего объяснения они кладут общепризнанное положение, что, само появление этой анизотропии обусловлено совместным действием спин-орбитальной связи, частичного замораживания орбитальных моментов неоднородными кристаллическими полями и орбитальным обменным взаимодействием соседних атомов. Таким образом, самопроизвольная намагниченность кристалла “чувствует” ионную решетку через орбитальное движение магнитных электронов. Спины, участвующие в намагниченности, взаимодействуют с орбитальным движением с помощью спин-орбитальнойсвязи, а орбитальное движение связано с решеткой
полем лигандов.

Микроскопическая энергия, возникающая благодаря этому механизму, может быть в свою очередь двух типов:

1) спин-орбитальная связь, которая зависит от спиновых состояний
двух или более ионов-носителей магнитного момента (парная модель
магнитной анизотропии);

2) связь, зависящая от спинового состояния только отдельных ионов
(одноионная модель магнитной анизотропии). Последний механизм оказывается наиболее близким к реальной ситуации, которая имеет место в неметаллических антиферро - и ферримагнетиках, в которых магнитноактивные ионы находятся в окружении магнитно-нейтральных анионов. Под действием поля лигандов, симметрия которого определяется типом кристалла, происходит расщеплениеуровней магнитного иона. В результате основному состоянию в зависимости от структуры кристаллической решетки будут соответствовать различные типы уровней, что приводит к магнитной анизотропии кристалла с магнитным порядком.

§ 3.Магнитострикция при техническом намагничивании

Известно, что в процессе технического намагничивания происходит смещение границ доменов и вращение вектораI_s. Рассмотрим, как эти процессы влияют на изменение длины кристалла с положительной константой магнитной анизотропииK₁.

Пусть внешнее магнитное поле параллельно оси [110] и в исходном состоянии объемыV_i доменов, намагниченных вдоль шести направлений легкого намагничивания, равновелики: V⁰₁₀₀= V⁰_I00 =V⁰_0I0 =V⁰₀₀₁ =V⁰_{0I 0} =V⁰_00I =1/6 V, где V – объем кристалла.

а) Смещение 180° доменных границ. При этом домены, намагниченные вдоль направлений [100]и_{010], поглощаются доменами,намагниченными в направлениях [100] и [010]. Изменения длины при смещении 180° доменных границ не происходит.

После того как смещение этих границ заканчивается, объемы
доменов равны

V⁰_I00= V⁰_0I0 =0

При этом средняя намагниченность кристалла

I= 2/3 (2) ^{- ½} I_s

б) Смещение90° границ. При этом домены, намагниченные
вдоль направлений [100] и [010], поглощают домены, намагниченные в направлениях [001] и [001]. В конце этого процесса объемыдоменов равныV₁₀₀=V₀₁₀=V/2,V₀₀₁=V_00I=0и средняя намагниченность кристалла

I = (2) ^{- ½}I_s

Отноносительное изменение длины,вызванное смещением 90° границ, будет при этом равно

∆l/l=1/3[(dl/l)_[001] – (dl/l)_[100]]=1/3[(dl/l)_[001] – (dl/l)_[010]] = (1/3)(3/4) l₁₀₀ = ¼ l₁₀₀

(28)

гле

(dl/l)_[001] (a₁ = a₂ = 0, a₃ = 1 ),

(dl/l)_[100] (a₂ = a₃ = 0, a₁ = 1 ),

(dl/l)_[010] (a₁ = a₃ = 0, a₂ = 1 ),

Отметим, что формула (28) определяет лишь конечное изменение длины, соответствующее намагниченностиI= (2) ^{- ½} I_s, при которой заканчивается процесс смещения 90° границ при условии,что вклад в намагниченность от процессов вращения еще пренебрежимо мал.
в) Вращение. Если процессы смещения 180 и 90 границ заканчиваются в слабых магнитных полях, при которых вклад в намагниченность от процессов вращения пренебрежимо мал, томожно считать, что при дальнейшем росте магнитного поля вращение векторов намагниченности доменов к оси [110] происходитв плоскости (001) .ПустьJ - угол между направлением намагниченности доменови полем. Тогда намагниченность вдоль поля Н равнаI=I_s cos J. Относительное удлинение вдоль оси [110] будет

(d l/l)_[110] = - 1/2l₁₀₀ + 3/4l₁₀₀(a²₁+a²₂) + 3/2l_111a1a2 ,

где a₁ = cos(p/4-J), a₂ = sin(p/4-J) , откуда

(d l/l)_[110] = ¼ l₁₀₀ + ¾ l₁₁₁(2cos^2J -1) » ¼ l₁₀₀ + ¾ l₁₁₁(2(I/I_s)² -1).

Метод измерений и описание установки

На исследуемые в работе ферромагнитные образцы, наклеены проволочные тензодатчики, изготовленные из тонкой константановой проволоки. Константан имеет очень малый температурный коэффициент омического сопротивления и пригоден для выполнения прецизионных измерений. В результате явление магнитострикции при намагничивании образца изменяются и линейные размеры тензодатчика, что приводит к изменению его омического сопротивления. По величине изменения омического сопротивления можно судить о величине магнитострикции. Коэффициент пропорциональности изменения омического сопротивления тензодатчика называют коэффициентом тензочуствительности.

На рис.2 приведена электрическая схема установки для измерения магнитострикции. Схема собрана в виде стенда с клеммами для подключения внешних приборов, а именно: источника постоянного напряжения 10В. и микровольтметра постоянного тока. Через клеммы также подключается тензодатчик исследуемого образца и источник постоянного магнитного поля (соленоид). Измерительный проволочный тензодатчик ИТД является одним из плеч измерительного моста, во второе плечо которого включен компенсационный тензодатчик КТД, наклеенный на стальную полоску, находящуюся вне магнитного поля. Два других плеча измерительного моста образованы прецизионными резисторами R1и R2 . Потенциометр R3служит для грубой компенсации моста, а реоход R4для точной компенсации. К диагонали измерительного моста через подвижный контакт реохода и клеммы x3,x4 “мкВ”

Подключается внешний микровольтметр. Резистор R5задает ток питания датчиков. На стенде размещен также переменный резистор R6 для регулировки тока в соленоиде и, соответственно, амплитуды магнитного поля в нем. Конструктивно-технологические особенности выполнения измерений магнитострикции.

Измерение магнитострикции является прецизионным процессом, в силу малости измеряемой величены. Даже у никеля, имеющего одну из самых больших величин магнитострикции, она составляет всего 30x10^-6. Поэтому при питании тензодатчиков током порядка 5мА, разбаланс моста составляет в зависимости от величены l от 1 до 10 мкВ, что соответствует изменению сопротивления тензодатчика 10^-4-10^-3 Ом. Для сравнения: величина термоЭДС контакта медь-конктантан – 30 мкВ/град С, а переходные сопротивления контактов могут достигать величин десятых долей Ома, т.е. ,по крайней мере, два мешающих фактора существенно превосходят измеряемую величину. Основные способы отстройки от мешающих факторов использованные в стенде:

-размещение контактов индуцирующих термоЭДС в соседних плечах моста для компенсации ее;

-использование скользящего контакта реохода (контакта с большим переходным сопротивлением) в высокоомной потнциалометрической цепи;

-обеспечение стабильного температурного режима за счет изготовления соленоида с большим запасом по мощности (во избежание его нагрева) и удаление его от измерительной схемы.

Для выполнения работы необходимы:

• стенд контроля,
• амперметр постоянного тока,
• микровольтметр постоянного тока или гальванометр,
• источник постоянного напряжения.

В качестве образцов работе используется ленты из никеля (образец №1) и лента из электротехнической стали марки 3414 толщиной 0,35 мм, вырезанной вдоль направления проката, совпадающего с направлением магнитной и кристаллографической текстуры (образец №2) и поперек направления проката, т.е. поперек направления магнитной текстуры (образец №3). Порядок выполнения измерений следующий:

1. Подготовить к измерениям рабочее место.

1. Подключить к клеммам “мкВ” микровольтметр постоянного напряжения к клеммам “U пит” источник постоянного напряжения, установив на нем напряжение 10 В. К клеммам “соленоид” подключить последовательно соедененные амперметр постоянного тока и соленоид. К клеммам “ИТД” подключить выводы тензодатчика, наклеенного на образце №1.
2. Установить переключатель пределов измерения микровольтметра в положение максимальной величине напряжения. Переключатель пределов измерения амперметра установить в положение “2А”, а ручку резистора регулировки тока соленоида в крайнее левое положение, соответствуещее минимальному току.

1. Выполнить измерения магнитострикции.
1. Включить в сеть микровольтметр и источник питания и дать ему прогретьсяв течении 5-10 мин.
2. С помощью резисторов “компенсация грубо” и реохода “компенсация точно” скомпенсировать измерительный мост – добиться минимальных показателей микровольтметра. Постепенно увеличивая чувствительность микровольтметра, довести ее до предела “100 кВ”.
3. Изменяя ток в соленоиде от минимального значения до 2А записать показания вольтметра, соответствуещее 5-6 точкам значений тока в соленоиде.
4. Выполнить измерения в том же порядке для образцов 2 и 3.

Примечания: 1. Перед заменой образца тензодатчика выключить источник напряжения, а ручки управления приборов установить в положение соответстстаующее п.1.2.

2. В случае, если не удается установить стрелку

микровольтметра на нулевое положение в процессе компенсации моста, допускается производить отсчет показаний относительно полученного (ненулевого) значения шкалы.

3. Замену образов производить при выключенном источнике питания микровольтметра.

1. Рассчитать величину магнитострикции, соответствующую показаниям микровольтметра.
2. По номиналам резисторов, указанным в схеме на рис.2 рассчитать ток тензодатчика.
3. Зная разбаланс моста в мкВ и ток через тензодатчик рассчитать разбаланс моста в Омах и определить соответствующую этому разбалансу магнитострикцию, используя соотношение:

l=∆l/l=g(∆R/R),

где ∆R – разбаланс моста в Омах.

R = 200 Oм – сопротивление тензодатчика,

g= 2 - коэффициент тензочувствительности.

4. Построить зависимость g =f(H)для всех образцов (постоянная соленоида К = 100 Э/А = H/J, где Н – амплитуда магнитного поля, J – ток соленоида).
5. Объяснить различия в зависимостях g =f(H) для образцов из электротехнической стали, вырезанных вдоль и поперек проката.

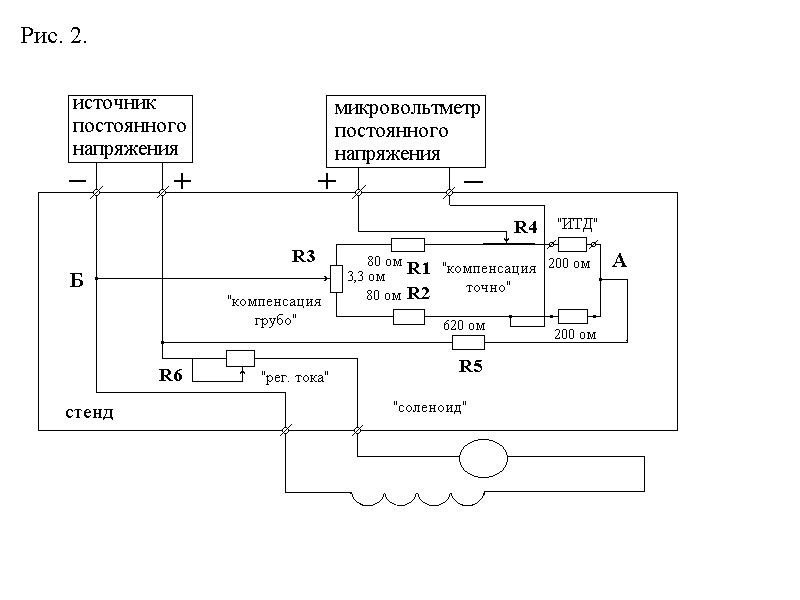
Рис. 2. Электрическая схема установки для измерения магнитострикции.

1. Вонсовский С.В. Магнетизм: “Наука”, 1971,
2. Ивановский В.И. Физика магнитных явлений, Издательство Московского университета, 1981
3. Г.Рейнбот. Магнитные материалы и их применение. Перевод с немецкого Л. Энергия, 1974, с. 375-380.

1. Что такое магнитострикция ? Какова ее величина ? Чем явление магнитострикции отличается от пъезоэффекта ?
2. Вследствие чего возникают магнитострикционные деформации ?
3. Какова природа магнитной анизотропии ?
4. Какие оси в кубическом кристалле будут ОЛН, а какие ОТН ? Почему ?
5. Какие процессы влияют на изменение длины кристалла с положительной константой магнитной анизотропииK₁ ?
6. Зная плотность свободной энергии можно сосчитать всю термодинамику системы. Чему равна плотность свободной энергии деформированного кристалла, намагниченного до насыщения?
7. Как зависят константы магнитной анизотропии от вектора намагниченности в приближении молекулярного поля?
8. Вектор спонтанной намагниченности I_sвращается в плоскости (100) монокристалла кубической системы, j - угол между I_sи крисаллографичеким направлением [001]. Вывести выражение для магнитострикции в функции угла j в направлении [111].