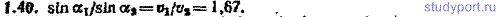1.21. Радиус-вектор частицы изменяется со временем по закону: r=3t²e_x+2te_y+1e_z (м). Найти: а) скорость v и ускорение w частицы, б) модуль скорости v в момент t=1 с, в) приближенное значение пути s, пройденного частицей за 11-ю секунду движения.

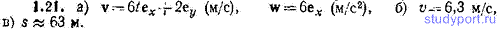
1.22. Частица движется со скоростью v=1e_x+2te_y+3t²e_z (м/с). Найти: а) перемещение Δr частицы за первые 2 секунды ее движения, б) модуль скорости v в момент t=2 с.

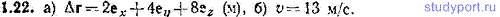
1.23. Частица движется со скоростью v=at(2e_x+3e_y+4e_z) (a =1,00 м/с²). Найти: а) модуль скорости v частицы в момент времени t=1,00 с, б) ускорение частицы w и его модуль w, в) путь s, пройденный частицей с момента t₁=2,00 с до момента t₂=3,00 с, г) какой характер имеет движение частицы.

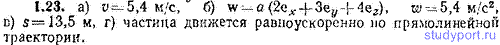
1.24. Лифт начал подниматься с постоянным ускорением w=1,00 м/с². Спустя время t=1,00 с от потолка кабины лифта отделился и стал падать шуруп. Определить: а) время Δt падения шурупа до удара о пол кабины, б) путь s, пройденный шурупом за время Δt в системе отсчета, связанной с Землей. Высота кабины лифта h=2,75 м.

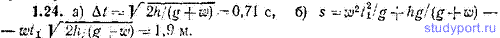
1.25. Известна функция v(t) для частицы, движущейся по криволинейной траектории. Написать выражение для радиуса кривизны R траектории в той точке, в которой частица находится в момент t?

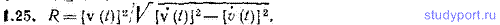
1.26. Частица движется равномерно по криволинейной траектории. Модуль ее скорости равен v. Найти радиус кривизны R траектории в той точке, где модуль ускорения частицы равен w.

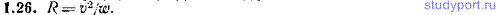
1.27. По какой траектории движется частица в случае, если ω_τ = 0, ω_n = const?

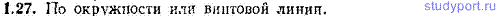
1.28. В некоторый момент времени t компоненты скорости v частицы имеют значения (1,00, 2,00, -3,00) (м/с), а компоненты ускорения w — (-3,00, 2,00, 1,00) (м/с²). Найти: а) значение выражения dv/dt в момент t, б) радиус кривизны R траектории в той точке, в которой частица находится в момент t.

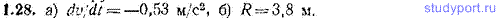
1.29. Точка движется вдоль оси x, причем координата x изменяется по закону x=a cos(2π/T)t. Найти: а) выражения для проекций на ось х скорости v и ускорения w точки, б) путь s₁, пройденный точкой за промежуток времени от t=0 до t=T/8, в) путь s₂, пройденный точкой за промежуток времени от t=T/8 до t=T/4, г) путь s, пройденный точкой за промежуток времени от t=0 до t=T.

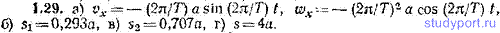
1.30. Компоненты скорости частицы изменяются со временем по законам: v_x=a cos ωt, v_y=a sin ωt, v_z=0, где а и ω — константы. Найти модули скорости v и ускорения w, а также угол α между векторами v и w. На основании полученных результатов сделать заключение о характере движения частицы.

1.31. Зависимость координат движения частицы от времени имеет вид x=a cos ωt, y=a sin ωt, z=0 (а и ω — константы). а) Определить радиус-вектор r, скорость v и ускорение w частицы, а также их модули. б) Вычислить скалярное произведение векторов r и v. Что означает полученный результат? в) Вычислить скалярное произведение векторов r и w. Что означает полученный результат? г) Найти уравнение траектории частицы. д) В каком направлении движется по траектории частица? е) Охарактеризовать движение частицы. ж) Как изменится движение частицы, если в выражении для y изменить знак на обратный?

1.32. Небольшое тело (материальная точка) брошено из точки О под углом α к горизонту с начальной скоростью v₀ (рис. 1.1). Пренебрегая сопротивлением воздуха, найти: а) время полета τ, б) дальность полета l, в) наибольшую высоту поднятия тела h, г) уравнение траектории тела в координатах x', y', д) значения |dv/dt| и d|v|/dt в вершине траектории, е) радиус кривизны R траектории в точках О и О'. Точки бросания и падения считать лежащими на одном уровне.

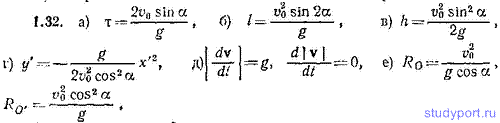
1.33. Тело брошено под углом к горизонту с начальной скоростью v₀. Пренебрегая сопротивлением воздуха, найти среднее значение скорости <v> за первые τ секунд полета.

1.34. Под каким углом α к горизонту нужно установить ствол орудия, чтобы поразить цель, находящуюся на расстоянии l=10,0 км, если начальная скорость снаряда v₀=500 м/с? Сопротивлением воздуха пренебречь.

1.35. Известны: функция f(s), определяющая зависимость производной dv/dt от пройденного частицей пути s, модуль скорости v₀ в начале пути. Написать выражение для v(s) — модуля скорости, которую имеет частица, пройдя путь s.

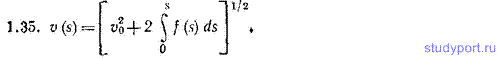
1.36. Дана функция v(s), определяющая зависимость модуля скорости частицы от пройденного частицей пути s. Написать выражение для времени t, затрачиваемого частицей на прохождение пути s.

1.37. Зависимость модуля скорости частицы v от пройденного частицей пути s определяется функцией v(s)=v₀-bs. а) Найти зависимость s от времени t. б) Определить зависимость v от t. в) Написать приближенные выражения для s(t) и v(t), справедливые для t<<1/b.

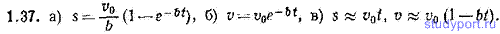
1.38. Модуль скорости частицы изменяется со временем по закону v=v₀e^-bt. Каков физический смысл константы b?

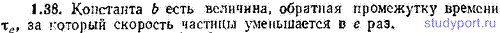
1.39. Лодка пересекает реку с постоянной относительно воды, перпендикулярной к берегам скоростью v=0,300 м/с. Ширина реки равна b=63,0 м. Скорость течения изменяется по параболическому закону u=u₀-4u₀(x-b/2)²/b², где х — расстояние от берега, u₀ — константа, равная 5,00 м/с. Найти снос s лодки вниз по течению от пункта ее отправления до места причала на противоположном берегу реки.

1.40. Ось x на рис. 1.2 служит границей между участком, поросшим травой, и участком, покрытым рыхлым песком. Пешеходу нужно попасть из пункта А в пункт В. По траве пешеход может идти со скоростью v₁=5,00 км/ч, по песку — со скоростью v₂=3,00 км/ч. Чтобы совершить переход за самое короткое время, пешеход выбирает ломаный путь АОВ. При каком соотношении между синусами углов α₁ и α₂ время движения пешехода из A в B будет минимальным?