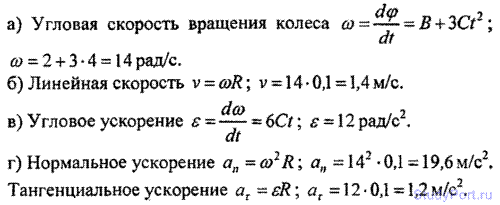1.41. Найти угловую скорость w: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т = 88 мин. Какова линейная скорость v движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии h = 200 км от поверхности Земли?
Решение:
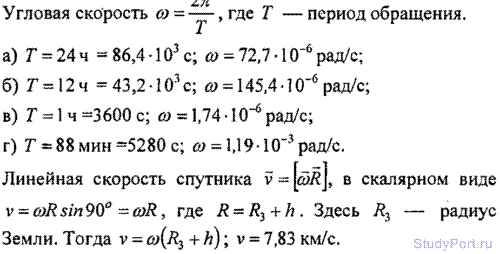
1.42. Найти линейную скорость v вращения точек земной поверхности на широте Ленинграда (ф = 60°).
Решение:
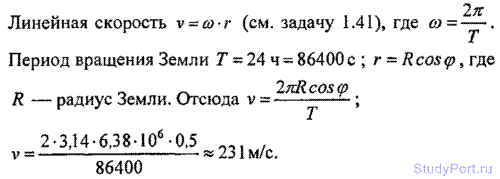
1.43. С какой линейной скоростью должен двигаться самолет на экваторе с востока на запад, чтобы пассажирам этого самолета Солнце казалось неподвижным?
Решение:

1.44. Ось с двумя дисками, расположенными на расстоянии l = 0,5м друг от друга, вращается с частотой п-1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол (ф = 12°. Найти скорость v пули.
Решение:

1.45. Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше линейной скорости v2 точки, лежащей на расстоянии r = 5 см ближе к оси колеса.
Решение:
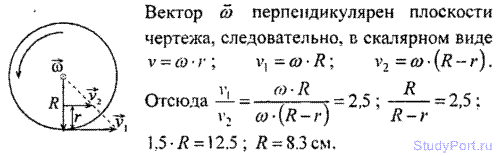
1.46. Колесо, вращаясь равноускоренно, достигло угловой скорости w-20рад/с через N = 10 об после начала вращения. Найти угловое ускорение е колеса.
Решение:

1.47. Колесо, вращаясь равноускоренно, через время t = 1мин после начала вращения приобретает частоту п = 720 об/мин. Найти угловое ускорение E колеса и число оборотов N колеса за это время.
Решение:
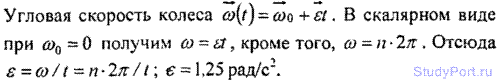
1.48. Колесо, вращаясь равнозамедленно, за время t = 1мин уменьшило свою частоту с n1 =300 об/мин до n2 =180 об/мин. Найти угловое ускорение е колеса и число оборотов N колеса за это время.
Решение:

1.49. Вентилятор вращается с частотой п = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
Решение:
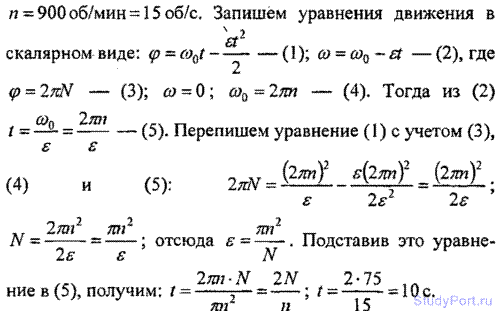
1.50. Вал вращается с частотой n = 180об/мин. С некоторого момента вал начинает вращаться равнозамедленно с угловым ускорением E = 3 рад/с2. Через какое время t вал остановится? Найти число оборотов N вала до остановки.
Решение:
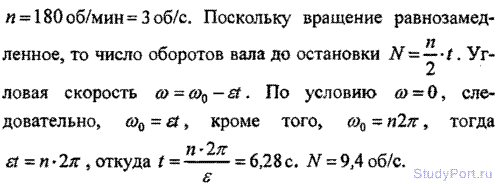
1.51. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением аr = 5 см/с2. Через какое время t после начала движения нормальное ускорение аn точки будет: а) равно тангенциальному; б) вдвое больше тангенциального?
Решение:
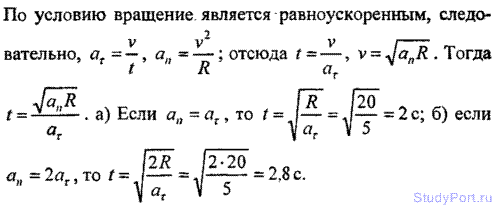
1.52. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а.. Найти тангенци ускорение ar точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки у = 79,2 см/с.
Решение:

1.53. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением аr. Найти нормальное ускорение аn точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 10 см/с.
Решение:


1.54. В первом приближении можно считать, что электрон в атоме водорода движется по круговой орбите с линейной скоростью v. Найти угловую скорость w вращения электрона вокруг ядра и его нормальное ускорение аn. Считать радиус орбиты r = 0,5 *10-10m и линейную скорость электрона на этой орбите v = 2,2*106 м/с.
Решение:
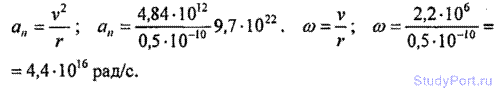
1.55. Колесо радиусом R = 10 см вращается с угловым ускорением E = 3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость w ; б) линейную скорость v; в) тангенциальное уско аi; г) нормальное ускорение ап; д) полное ускорение а; е) угол а, составляемый вектором полного ускорения с ради колеса.
Решение:
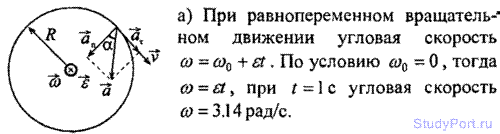

1.56. Точка движется по окружности радиусом R = 2см. Зависимость пути от времени дается уравнением s = Сt3, где С = 0,1 см/с3. Найти нормальное an и тангенциальное аi ускоре точки в момент, когда линейная скорость точки v = 0,3 м/с.
Решение:
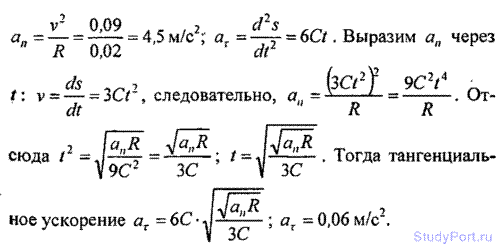
1.57. Точка движется по окружности так, что зависимость пути от времени дается уравнением s = A-Bt + Ct2, где В = 2 м/с и С = 1 м/с2. Найти линейную скорость v точки, ее тангенциальное aг, нормальное ап и полное а ускорения через время t = 3с после начала движения, если известно, что при t' = 2 с нормальное ускорение точки а'п = 0,5 м/с2.
Решение:
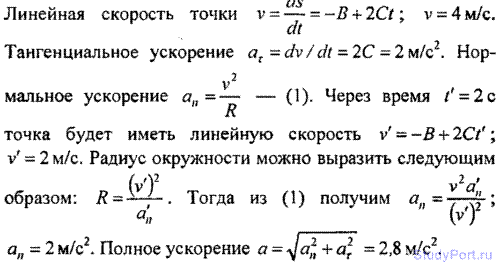
1.58. Найти угловое ускорение s колеса, если известно, что через время t = 2 с после начала движения вектор полного уско точки, лежащей на ободе, составляет угол а = 60° с вектором ее линейной скорости.
Решение:
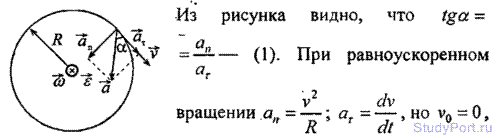
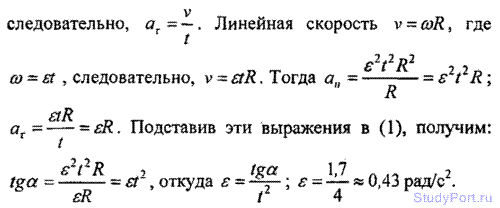
1.59. Колесо вращается с угловым ускорением E = 2рад/с2. Через время t = 0,5 с после начала движения полное ускорение колеса а-13,6 см/с2. Найти радиус R колеса.
Решение:

1.60. Колесо радиусом R = 0,.1м вращается так, что зави угла поворота радиуса колеса от времени дается уравнением ф = А + Bt + Ct2, где В = 2 рад/с и С = 1 рад/с\ Для точек, лежащих на ободе колеса, найти через время / = 2 с после начала движения: а) угловую скорость со; б) линейную скорость v; в) угловое ускорение с; г) тангенциальное ат и нормальное аи ускорения.
Решение: