3.21. Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу А надо совершить, чтобы остановить диск?
Решение:
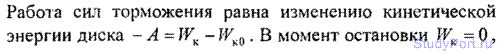
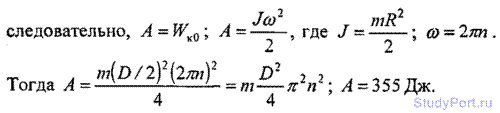
3.22. Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, WK = 60 Дж. Найти момент импульса L вала.
Решение:

3.23. Найти кинетическую WK энергию велосипедиста, еду со скоростью v = 9км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m0 = 3 кг. Колеса велосипеда считать обручами.
Решение:
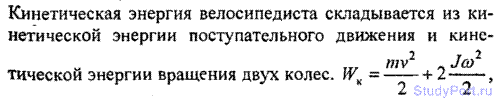
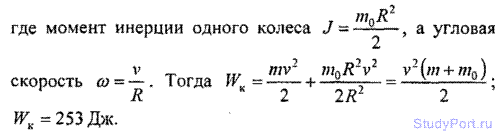
3.24. Мальчик катит обруч по горизонтальной дороге со скоростью v = 7,2 км/ч. На какое расстояние s может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100м пути.
Решение:

3.25. С какой наименьшей высоты h должен съехать вело, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом R = 3м*, и не оторваться от дорожки в верхней точке петли? Масса велоси вместе с велосипедом m = 75 кг, причем на колеса приходится масса m0 = 3 кг. Колеса велосипеда считать обруча.
Решение:

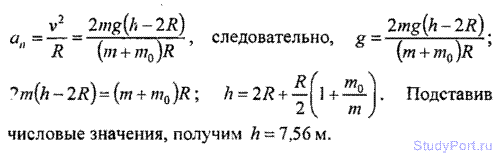
3.26. Медный шар радиусом R = 10 см вращается с частотой n= 2 об/с вокруг оси, проходящей через его центр. Какую работу А надо совершить, чтобы увеличить угловую скорость w вращения шара вдвое?
Решение:

3.27. Найти линейные ускорения а центров масс шара, диска и обруча, скатывающихся без скольжения с наклонной плос. Угол наклона плоскости а = 30°, начальная скорость всех тел v0 =0. Сравнить найденные ускорения с ускорением тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение:

3.28. Найти линейные скорости v движения центров масс шара, диска и обруча, скатывающихся без скольжения с наклон плоскости. Высота наклонной плоскости h = 0,5 м, началь скорость всех тел v0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Решение:

3.29. Имеются два цилиндра: алюминиевый (сплошной) и свинцовый (полый) — одинакового радиуса R = 6 см и одина массы m = 0,5 кг. Поверхности цилиндров окрашены оди. Как, наблюдая поступательные скорости цилиндров у ос наклонной плоскости, можно различить их? Найти мо инерции J1 и J2 этих цилиндров. За какое время t каждый цилиндр скатится без скольжения с наклонной плоскости? Высота наклонной плоскости h = 0,5 м, угол наклона плоскости а = 30°, начальная скорость каждого цилиндра v0 = 0.
Решение:

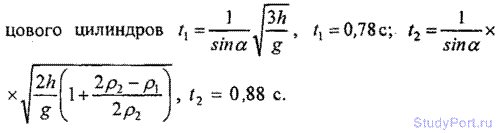
3.30. Колесо, вращаясь равнозамедленно, уменьшило за время t = 1мин частоту вращения от n1 =300 об/мин до n2 = 180 об/мин. Момент инерции колеса J = 2кгм2. Найти угловое ускорение е колеса, момент сил торможения М, ра А сил торможения и число оборотов N, сделанных коле за время t = 1 мин.
Решение:

3.31. Вентилятор вращается с частотой n = 900 об/мин, После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 15 об. Работа сил торможения А = 44,4 Дж. Найти момент инерции J вентилятора и момент сил торможения М.
Решение:

3.32. Маховое колесо, момент инерции которого J = 245кг*м2, вращается с частотой n = 20об/с. После того как на колесо перестал действовать вращающий момент, оно оста, сделав N =1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия враща момента до остановки колеса.
Решение:

3.33. По ободу шкива, насаженного на общую ось с маховым колесом, намотана нить, к концу который подвешен груз массой m = 1 кг. На какое расстояние h должен опуститься груз, чтобы колесо со шкивом получило частоту вращения n = 60 об/мин? Момент инерции колеса со шкивом J = 0,42 кгм2, радиус шкива R = 10 см.
Решение:

3.34. Маховое колесо начинает вращаться с угловым ускоре e = 0,5 рад/с2 и через время t1 = 15 с после начала движения приобретает момент импульса L = 73,5 кгм2/с. Найти кинети энергию WK колеса через время t2 = 20 с после начала движения.
Решение:
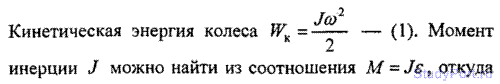

3.35. Маховик вращается с частотой n = 10 об/с. Его кинети энергия WK = 7,85 кДж. За какое время t момент сил М = 50Нм, приложенный к маховику, увеличит угловую ско со маховика вдвое?
Решение:

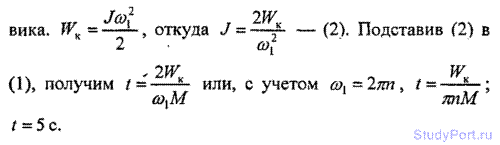
3.36. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 К. Какую кинетическую энергию WK будет иметь диск через время t = 5 с после начала действия силы?
Решение:
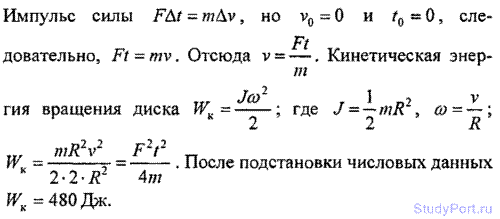
3.37. Однородный стержень длиной l = 1 м подвешен на гори оси, проходящей через верхний конец стержня. На какой угол а надо отклонить стержень, чтобы нижний конец стержня при прохождении положения равновесия имел скорость v = 5 м/с?
Решение:

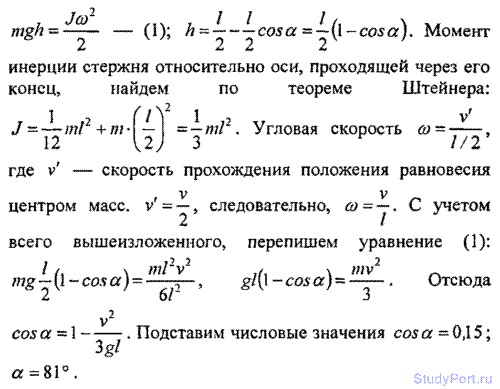
3.38. Однородный стержень длиной l = 85 см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую скорость v надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение:


3.39. Карандаш длиной l = 15 см, поставленный вертикально, падает на стол. Какую угловую скорость w и линейную ско v будет иметь в конце падения середина и верхний конец карандаша?
Решение:

3.40. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n1 =10 об/мин. Человек массой m0 =60 кг стоит при этом на краю платформы. С какой частотой n2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.
Решение:


