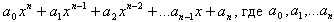Многочлен с одной переменной – это многочлен вида:

, где n - коэффициенты, а х – переменная.


Примеры:

.

 
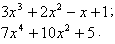Во втором примере коэффициенты при x³ и x  равны нулю.

Наивысшая степень переменной, входящих в многочлен одночленов называется степенью многочлена. Так в первом примере степень многочлена равна 3, а во втором - 4

Обозначают многочлен степени n с одной переменной так: .

 

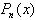Корнем многочлена с одной переменной 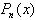, называют те значения переменной x, при которых многочлен обращается в ноль. Иными словами, решение уравнения 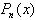=0.

Так, корнем многочлена 2x+6 является число -3. Так как -3 является решением уравнения 2x+6=0.

 

Не все многочлены имеют действительные корни. Рассмотрим это на примере квадратного трехчлена.

 

Пример 1: Найти корни квадратного трехчлена .

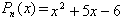Найдем корни, решив квадратное уравнение:

.

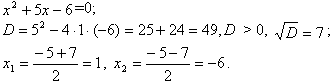Итак, многочлен имеет два действительных корня.

 

Пример 2:  Найти корни квадратного трехчлена .

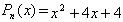Найдем корни, решив квадратное уравнение

.

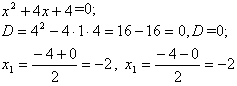Итак, мы видим, что два корня квадратного трехчлена совпадают. В этом случае говорят, что квадратный трехчлен имеет один двукратный корень.

 

Пример 3:  Найти корни квадратного трехчлена .

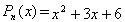Найдем корни, решив квадратное уравнение:

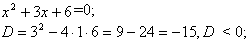
Так как дискриминант отрицательный, то действительных корней трехчлен не имеет.