Задание №1.
Произвести выборку 40 банков, пользуясь таблицей случайных чисел. Затем по отобранным единицам выписать значения факторного и результативного признаков.
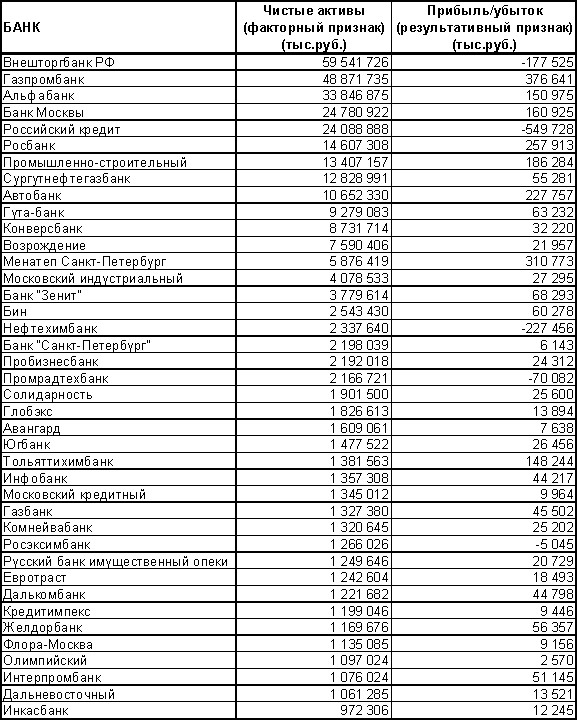
Задание №2.
Построить ряд распределения по факторному признаку. Число групп определить по формуле Стерджесса. По построенному ряду распределения рассчитать среднее арифметическое, моду, медиану, показатели вариации. Сформулировать выводы.
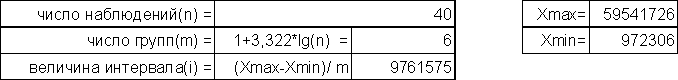
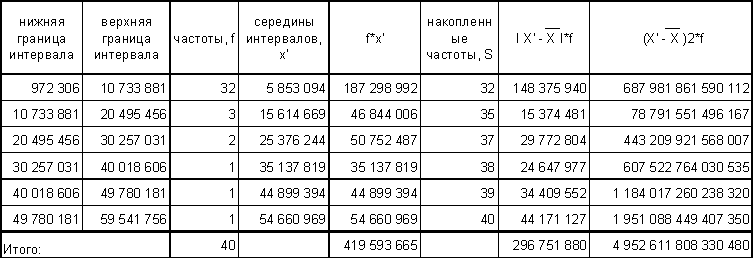


Выводы: Вариация факторного признака (чистых активов) для данной совокупности банков является значительной, индивидуальные значения отличаются в среднем от средней на 11 127 232 тыс. руб. *, или на 106,08%. Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних. Значение коэффициента вариации (106,08%) свидетельствует о том, что совокупность достаточно неоднородна.
Задание №3
Осуществить проверку первичной информации по факторному признаку на однородность. Исключить резко выделяющиеся банки из массы первичной информации.
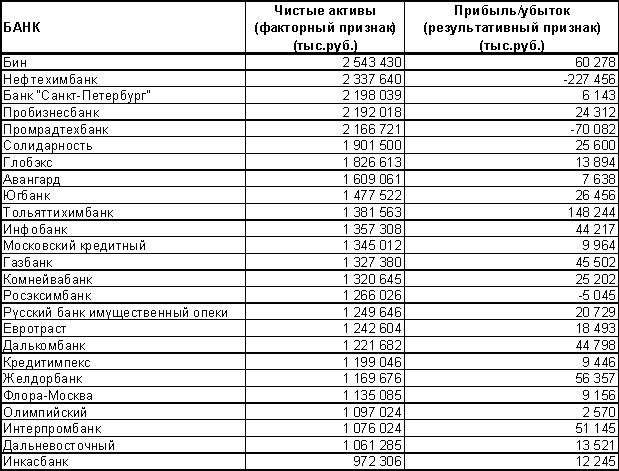
Проверка первичной информации по факторному признаку на однородность осуществлялась в несколько этапов по правилу 3 сигм. В результате была получена достаточно однородная совокупность (все единицы лежат в интервале (Xср. - 3s ; Xср. +3s), а коэффициент вариации меньше требуемых 33%), которая представлена ниже.
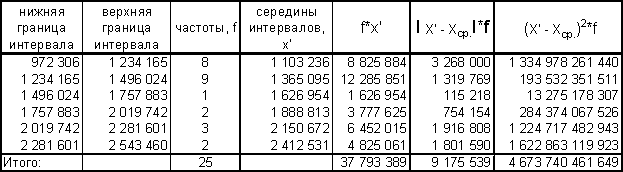
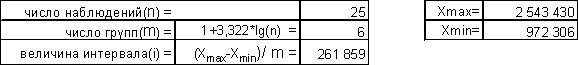



Задание №4
Предполагая, что данные банкам представляют собой 10% простую случайную выборку с вероятностью 0,954 определить доверительный интервал, в котором будет находиться средняя величина факторного признака для генеральной совокупности.
Xср. – D Xген. ср. ? Xген. ср. ? Xср. + D Xген. ср.
Где Xср. – средняя выборочной совокупности, Xген. ср. – средняя генеральной совокупности, D Xген. ср. – предельная ошибка средней.
D Xген. ср. = t * μген. ср. Где t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки, μген. ср. – величина средней квадратической стандартной ошибки.
Находим t по таблице для удвоенной нормированной функции Лапласа при вероятности 0,954, t = 2.
μген. ср. = Ц ((s 2* (1- n/N) ) /n) Где s 2 – дисперсия, n – объем выборочной совокупности, N – объем генеральной совокупности.
N=n/0,1 n=25 N=250 s 2= 200 301 737 920 Xср. = 1 506 994 (я взял дисперсию и среднюю, рассчитанные по однородной совокупности по не сгруппированным данным) μген. ср. = 84 917 D Xген. ср. = 169 834 Xср. – D Xген. ср. = 1 337 161 Xср. + D Xген. ср. = 1 676 828 1 337 161 ≤ Xген. ср. ? 1 676 828 - искомый доверительный интервал
Задание №5
Проанализировать зависимость результативного признака от факторного признака.
Пункт №1
Установить факт наличия корреляционной зависимости с помощью групповой таблицы и ее направление, дать графическое отображение связи.
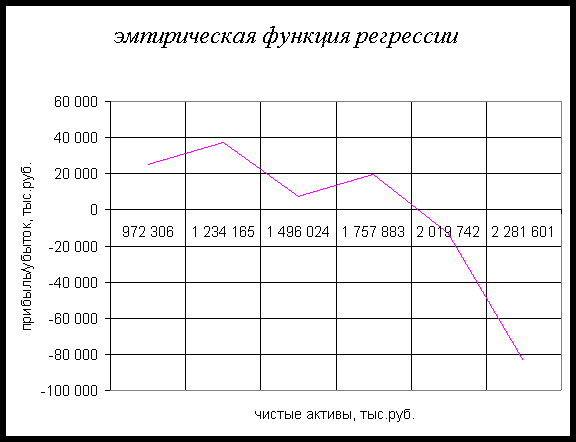
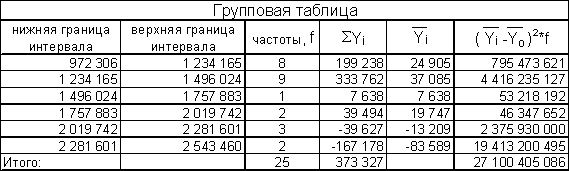
Как видно из данных групповой таблицы, с увеличением величины чистых активов банков уменьшается величина прибыли банков. Эмпирическая линия связи приближается, в общем, к прямой линии. Следовательно, можно предполагать наличие обратной линейной связи.
Пункт №2
Проверить правило сложения дисперсий и сформулировать вывод о степени влияния факторного признака на величину результативного признака.
Нижеследующие показатели были рассчитаны на основе данных групповой таблицы и вспомогательной таблицы (см. приложение 2) .
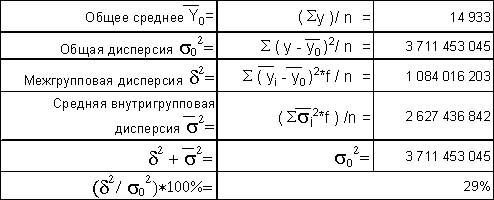
Правило сложения дисперсий проверено: общая дисперсия и сумма межгрупповой и средней внутригрупповой дисперсий совпадают. Из полученных данных можно сделать вывод, что на 29% вариация прибыли банков обусловлена различиями в величине их активов, а на 71% - влиянием прочих факторов. Таким образом, факторный признак (чистые активы банков) имеет среднее влияние на результативный признак (прибыль/убыток) .
Пункт №3
Измерить степень тесноты связи с помощью корреляционных отношений, проверить возможность использования линейной функции в качестве формы уравнения связи.

Все нижеследующие показатели рассчитаны с помощью ранее найденных данных и данных вспомогательной таблицы (см. приложение 2) .
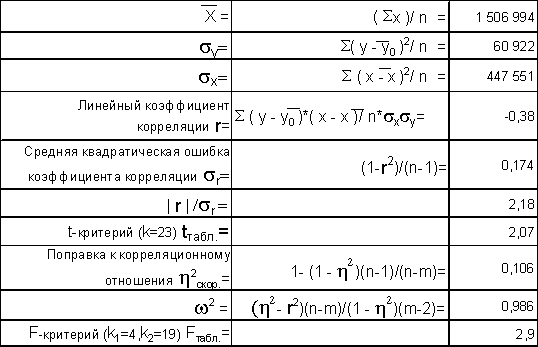
Значение линейного коэффициента корреляции (r = -0,38) свидетельствует об отсутствии тесной связи. Средняя квадратическая ошибка коэффициента корреляции s r =0,174, а ъ rъ /s r =2,18, так как ъ rъ /s r > tтабл. (2,18>2,07), то коэффициент корреляции можно считать существенным.
Корреляционное отношение (h =0,54) показывает незначительную тесноту связи. Значимость рассчитанного корреляционного отношения оценивается с помощью дисперсионного отношения, равного 1,568. Так как 1,568<2,74 (F-критерий = 2,74), то оценивать тесноту связи с помощью корреляционного отношения нельзя из-за его несущественности.
Рассчитанные здесь же коэффициент Фехнера (Кф= -0,28) и коэффициент корреляции рангов Спирмэна (r = -0,048) свидетельствуют о наличие слабой связи. Данные для расчета этих коэффициентов приведены во вспомогательной таблице (см. приложение 2) .
Для проверки возможности использования линейной функции определяется величина w 2 =0,986, она меньше табличного значения F-критерия (Fтабл. =2,9), поэтому гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается.
Итак, можно утверждать, что между факторным и результативным признаком существует слабая связь. На этом этапе можно было бы остановить исследование, так как очевидно, что был выбран факторный признак, не оказывающий существенного влияния на результативный. И построенная по нему модель связи вряд ли будет качественной и достоверной, и вряд ли будет иметь практическую пользу в экономическом смысле. Но я все же доведу исследование до конца.
Пункт №4
Рассчитать параметры уравнения регрессии, оценить его качество и достоверность, используя среднюю квадратическую ошибку. Дать оценку результатов исследования взаимосвязи в целом.
Определяется модель связи. График эмпирической функции регрессии и величина w 2 показывают наличие линейной связи, поэтому используется функция ŷ = a + bx.
b= (S xЧ y – nЧ x Ч y) / (S x2 - nЧ (x) 2) = -0,05
a= y - bЧ x = 93 099,35 ŷ = 93 099,35 – 0,05Ч x - модель связи.
Все данные для расчетов содержатся во вспомогательной таблице (см. приложение 2) .
Средняя квадратическая ошибка уравнения:
Sl = Ц (S (y-ŷ) 2/ (n-l) ) = 58 723, где ŷ – значения результативного признака, рассчитанные по уравнению связи, l – количество параметров уравнения регрессии.
(Sl / y) Ч 100 = (58723/14933) Ч 100=393% Полученное отношение значительно больше 15%, поэтому уравнение достаточно плохо отображает взаимосвязь двух признаков и не может быть использовано в практической работе.
По результатам исследования можно сделать вывод о том, что, хотя теоретически между чистыми активами банков и их прибылями должна существовать прямая тесная связь, на практике же мы показали наличие довольно слабого влияния факторного признака на результативный. Это не совпадение может объясняться рядом причин: во-первых, ошибочными теоретическими предположениями, во-вторых, некачественной, нерепрезентативной выборкой, и, наконец, в-третьих, ошибками, допущенными в исследовании, которых, может быть, не удалось избежать.

