9.21. Построить на одном графике кривые зависимости напряженности E электрического поля от расстояния r в интервале 1

ряженной, нитью с линейной плотностью заряда ? = 1,67мкКл/м; в) бесконечно протяженной плоскостью с поверхностной плотностью заряда ? = 25 мкКд '\г.

9.23. С какой силой F1 электрическое поле заряженной бесконечной плоскости действует на единицу длины заряженной бесконечно длинной нити, помешенной в это поле? Линейная плотность заряда на нити ? = ЗмкКл/м и поверхностная плотность заряда на плоскости ? = 20 мкКл/м".

9.24. С какой силой F1 на единицу длины отталкиваются две
одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда ? = ЗмкКл.'м, находящиеся на расстоянии r1 = 2 см друг от друга? Какую работу A1 на единицу длины надо совершить, чтобы сдвинуть эти нити до расстояния r2 = 1 см?
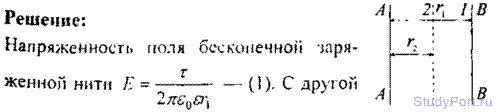

9.25. Две длинные одноименно заряженные нити расположены на расстоянии r = 10 см друг от друга. Линейная плотность заряда на нитях ?1 = ?2 = 10 мкКл/м. Найти модуль и направление напряженности Е результирующего электрического поля в точке, находящейся на расстоянии а = 10 см от каждой нити.
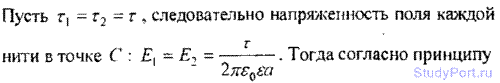 <
<
img src="/images/stories/tasks/Physics/electrostat/32.gif" width="376" height="258">
9.26. С какой силой FS на единицу площади отталкиваются
две одноименно заряженные бесконечно протяженные плоскости? Поверхностная плотность заряда на плоскостях ? = 0,3 мКл/м.
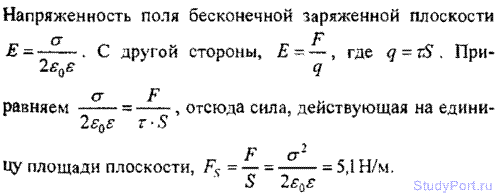
9.27. Медный шар радиусом R = 0,5 см помещен в масло. Плотность масла рм = 0,8 • 103 кг/м°. Найти заряд q шара, если в
однородном электрическом поле шар оказался взвешенным в масле. Электрическое поле направлено вертикально вверх п его напряженность Е = 3,6 МВ/м.

9.28. В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля Е = 60 кВ/м. Заряд капли
q = 2,4 * 10-9 СГСq. Найти радиус R капли.

9.29. Показать, что электрическое поле, образованное заряженной нитью конечной длины, в предельных случаях переходит в электрическое поле: а) бесконечно длинной заряженной нити; б) точечного заряда.

9.30. Длина заряженной нити l = 25 см. При каком предельном расстоянии а от нити по нормали к середине нити электрическое поле можно рассматривать как поле бесконечно длинной заряженной нити? Ошибка при таком допущении не должна превышать ? = 0,05. Указание: допускаемая ошибка
?=(E2-E1)/E2, где E2 — напряженность электрического поля бесконечно длинной нити, E1 — напряженность поля нити конечной длины.

9.31. В точке А, расположенной на расстоянии а = 5 см от бесконечно длинной заряженной нити, напряженность электрического поля E = 150 кВ/м. При какой предельной длине l нити найденное значение напряженности будет верным с точностью до 2%, если точка А расположена на нормали к середине нити? Какова напряженность ? электрического поля в точке А, если длина нити l = 20см? Линейную плотность заряда на нити конечной длины считать равной линейной плотности заряда на бесконечно длинной нити. Найти линейную плотность заряда ? на нити.


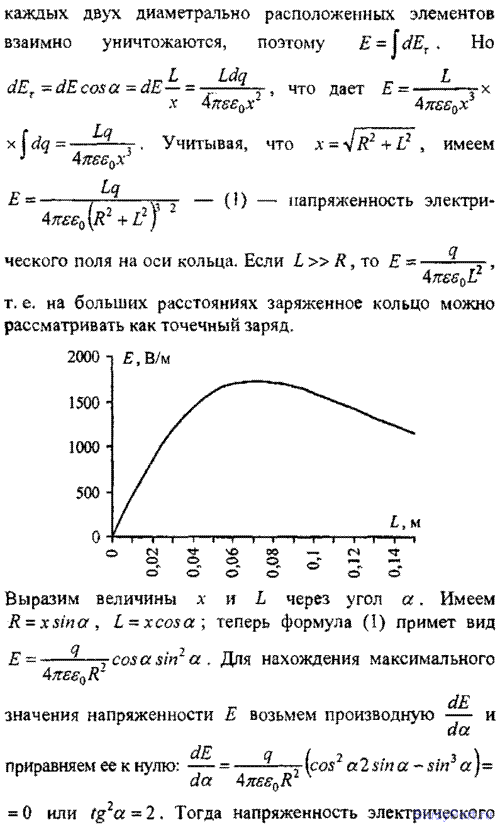
9.32. Кольцо из проволоки радиусом R = 10 см имеет отрицательный заряд q = -5нКл. Найти напряженности E электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях L, равных 0, 5, 8, 10 и 15см. Построить график Е = f(L). На каком расстоянии L от центра кольца напряженность ? электрического поля будет иметь максимальное значение?


9.33. Напряженность электрического поля на оси заряженного кольца имеет максимальное значение на расстоянии L от центра кольца. Во сколько раз напряженность электрического поля в точке, расположенной на расстоянии 0,5L от центра кольца, будет меньше максимального значения напряженности?

9.34. Показать, что электрическое поле, образованное заряженным диском, в предельных случаях переходит в электрическое поле: а) бесконечной заряженной плоскости; б) точечного заряда.

9.35. Диаметр заряженного диска D = 25 см. При каком предельном расстоянии а от диска по нормали к его центру электрическое поле можно рассматривать как поле бесконечно протяженной плоскости? Ошибка при таком допущении не должна превышать ? = 0,05. Указание: допускаемая ошибка ? = (E2-E1)/E2 где E1 — напряженность поля бесконечно протяженной плоскости, E2 — напряженность поля диска.

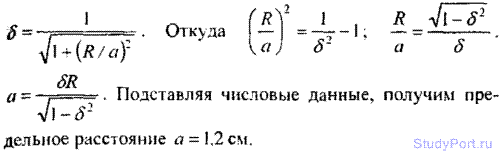
9.36. Требуется найти напряженность Е электрического поля в точке А, расположенной на расстоянии а = 5 см от заряженного диска по нормали к его центру. При каком предельном радиусе R диска поле в точке А не будет отличаться более чем на 2% от поля бесконечно протяженной плоскости? Какова напряженность Е поля в точке А, если радиус диска R = 10а? Во сколько раз найденная напряженность в этой точке меньше напряженности поля бесконечно протяженной плоскости?

9.37. Два параллельных разноименно заряженных диска с одинаковой поверхностной плотностью заряда на них расположены на расстоянии d = 1 см друг от друга. Какой предельный радиус R могут иметь диски, чтобы между центрами дисков поле отличалось от поля плоского конденсатора не более чем на 5%? Какую ошибку ? мы дотекаем, принимая для этих точек напряженноеib поля равном напряженности поля плоского кон-
денсатора при R
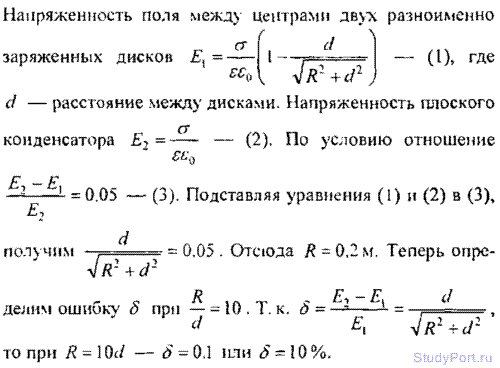
9.38. Шарик массой т = 40 мг, имеющий положительным заряд q = 1нКл, движется со скоростью v = 10 см/с. На какое расстояние может приблизиться шарик к положительному точечному заряду q0 = 1,33 нКл?
![]()

9.39. До какого расстояния r могут сблизиться два электрона, если они движутся навстречу друг другу с относительной
скоростью v1 = 106 м/с?


9.40. Протон (ядро атома водорода) движется со скоростью v = 7,7 * 106 м/с. На какое наименьшее расстояние r может приблизиться протон к ядру атома алюминия? Заряд ядра атома алюминия q = Ze, где Z — порядковый номер атома в таблице Менделеева и е — заряд протона, равный по модулю заряду электрона. Массу протона считать равной массе атома водорода. Протон и ядро атома алюминия считать точечными зарядами. Влиянием электронной оболочки атома алюминия пренебречь.


