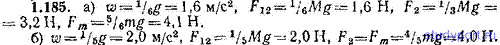1.167. Имеется однородный прямой круглый цилиндр. При каком отношении высоты цилиндра h к его радиусу R все три главных момента инерции будут одинаковыми?

1.168. Найти момент инерции однородного тела, имеющего форму диска, в котором сделан квадратный вырез. Одна из вершин выреза совпадает с центром диска. Радиус диска R=20,0 см, сторона квадрата a=10,0 см, масса тела m=5,00 кг. Имеется в виду момент относительно оси, перпендикулярной к диску и проходящей через его центр.
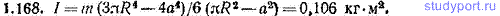
1.169. Имеется однородная тонкая пластинка, ограниченная контуром произвольной формы. Через одну из точек пластинки проведены три взаимно перпендикулярные реи, две из которых – x и y - лежат в плоскости пластинки, а ось z перпендикулярна к этой плоскости. соотношение между моментами инерции пластинки относительно этих осей,

1.170. Использовать ответ предыдущей задачи для нахождения момента инерции I тонкого однородного диска относительно оси, лежащей в плоскости диска и проходящей через его центр. Масса и радиус диска равны соответственно m и R. Момент инерции относительно оси, перпендикулярной к плоскости диска, считать известным. Сравнить полученный результат с ответом к задаче 1.165.

1.171. Однородная пластина имеет длину a=20,0 см, ширину b=10,0 см и толщину c=5,00 см. Масса пластины m=2,70 кг. Начало координат помещено в центр пластины, ось х направлена параллельно стороне а, ось у - параллельно стороне b, ось z - параллельно стороне с. Найти относительно этой системы координат компоненты тензора инерции пластины и написать сам тензор.
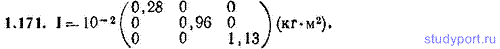
1.172. Имеются вектор а с компонентами ax=1, ay=2, az=3 и тензор второго ранга Т, все компоненты которого одинаковы и равны Tih=1. Найти компоненты вектора b, получающегося в результате умножения вектора a на тензор T (b=Ta).

1.173. Имеются произвольный вектор а с компонентами ax, ay, az и тензор второго ранга Е, (такой тензор называют единичным). Найти вектор b, получающийся в результате умножения вектора a на тензор E (b=Ea).

1.174. Вычислить компоненты тензора инерции и написать сам тензор для однородного шара радиуса R=10,0 см и массы m=25,0 кг для случая, когда начало координат помещается в центре шара.
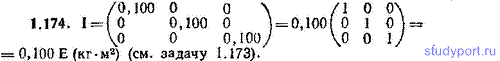
1.175. В каких случаях момент импульса М и угловая скорость ω вращающегося тела коллинеарны?
1.176. В каких случаях уравнение динамики вращательного движения может быть представлено в виде lω=N?
1.177. В каких случаях кинетическая энергия вращающегося тела определяется выражением T=lω2/2?
1.178. Пластина из задачи 1.171 вращается вокруг оси, проходящей через ее центр. Компоненты угловой скорости ωx=ωy=ωz=1,00 рад. Найти: а) модуль момента импульса пластины М и угол α между векторами ω и M, б) кинетическую энергию T пластины.
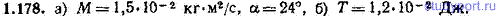
1.179. Две частицы одинаковой массы m, находящиеся все время на противоположных концах диаметра (рис. 1.31), движутся по окружности радиуса r с одинаковыми по модулю скоростями v1 и v2 [v1=v2=v(t)] а) Определить суммарный момент импульса М частиц относительно произвольной точки О (не обязательно лежащей в плоскости окружности). Выразить М через угловую скорость ω(t), с которой поворачивается диаметр, соединяющий частицы. б) Зависит ли М от выбора точки О?
1.180. Однородный шар радиуса R и массы m вращается с угловой скоростью ω вокруг оси, проходящей через его центр. Найти момент импульса M шара относительно произвольной точки O (рис. 1.32).

1.181. Тело произвольной формы падает, вращаясь, в однородном поле сил тяжести. Сопротивление среды отсутствует. Как ведет себя собственный момент импульса тела? (См. задачу 1.123)

1.182. Однородный цилиндр радиуса R и массы m катится без скольжения по горизонтальной плоскости. Центр цилиндра движется со скоростью v0 (рис. 1.33). Найти модуль момента импульса цилиндра относительно точек 1,2 и 3, которые лежат в перпендикулярной к цилиндру плоскости, проходящей через его центр.
1.183. Вычислить момент импульса Земли M0, обусловленный ее вращением вокруг своей оси. Сравнить этот момент с моментом импульса М, обусловленным движением Земли вокруг Солнца. Землю считать однородным шаром, а орбиту Земли — окружностью.
1.184. Горизонтально расположенный однородный цилиндр радиуса R вращается без трения вокруг оси, совпадающей с одной из его образующих. а) Указать положения цилиндра, в которых модуль углового ускорения цилиндра β максимален и минимален, б) Найти максимальное и минимальное значения β.

1.185. На горизонтальном столе лежат два тела, которые могут скользить по столу без трения. Тела связаны невесомой нерастяжимой нитью (рис. 1.34). Такая же нить, переброшенная через блок, связывает тело 2 с грузом массы m=0,500 кг. Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна M=1,00 кг. а) Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел w, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m. б) Определить те же величины, предполагая, что блок не вращается, а нить скользит по нему без трения. Сравнить полученные результаты.