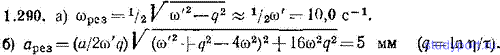1.271. Пренебрегая трением, определить частоту ω малых колебаний ртути, налитой в U-образную трубку с внутренним сечением S=0,500 см2 (рис. 1.41). Масса ртути m=136 г.

1.272. Деревянный молоток состоит из цилиндрического бойка радиуса R = 4,00 см и рукоятки длины l=90,0 см. Масса бойка m1 = 0,800 кг, масса рукоятки m2 = 0,600 кг. Молоток положен на два параллельных бруска (рис.). Найти период m малых колебаний этой системы.
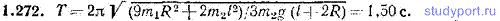
1.273. Бревно массы M=20,0 кг висит на двух шнурах длины l=1,00 м каждый (рис. 1.43). В торец бревна ударяет и застревает в нем пуля массы m=10,0 г, летящая со скоростью v=500 м/с. Найти амплитуду φm и период T возникших колебаний этой системы. Трением пренебречь.
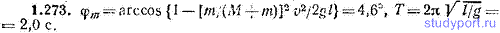
1.274. Шар массы m=2,00 кг подвешен к двум соединенным последовательно пружинам (рис. 1.44). Жесткость пружин равна: k1=1000 Н/м, k2=3000 Н/м. Пренебрегая массой пружин и трением, найти: а) частоту ω малых колебаний шара, б) амплитуду а колебаний, возникающих в том случае, если шар установить на уровне, при котором пружины не напряжены, и отпустить без толчка.
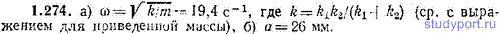
1.275. Блок показанного на рис. 1.45 устройства представляет собой сплошной однородный цилиндр, который может вращаться вокруг оси без ощутимого трения. Масса блока M=5,00 кг. Жесткость пружины k=1000 Н/м. Массой пружины и переброшенного через блок шнура можно пренебречь. Масса висящего на шнуре груза m=1,00 кг. Полагая, что проскальзывание шнура по блоку отсутствует, найти: а) частоту ω малых колебаний устройства, б) максимальную силу натяжения шнура слева (F1m) и справа (F2m) от блока в случае, когда амплитуда колебаний a=5,00 мм.
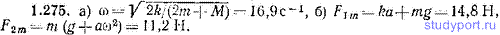
1.276. Два шара массами и m1 и m2 могут скользить без трения по тонкому горизонтальному стержню (рис. 1.46). Шары связаны невесомой пружиной жесткости k. Сместив шары в противоположные стороны, их отпускают без толчка. Определить: а) как ведет себя центр масс системы, б) частоту ω возникших колебаний, в) максимальное значение относительной скорости шаров vmax, если начальное относительное смещение шаров равно a.

1.277. Два шара массами m1 и m2 могут скользить без трения по длинной натянутой горизонтально проволоке (см. рис. 1.46). Шары связаны невесомой пружиной жесткости k. Первоначально система неподвижна и пружина не напряжена. Первому шару сообщается импульс p0=m1v0. Определить: а) скорость vC центра масс системы, б) энергию Eпост поступательного и Eколеб колебательного движения системы, в) частоту ω и амплитуду a колебаний.
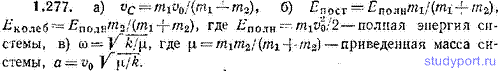
1.278. Однородный диск массы m=3,00 кг и радиуса R=20,0 см скреплен с тонким стержнем, другой конец которого закреплен неподвижно (рис. 1.47). Коэффициент кручения стержня (отношение приложенного вращающего момента к углу закручивания) k=6,00 Н*м/рад. Определить: а) частоту ω малых крутильных колебаний диска, б) амплитуду φm и начальную фазу α колебаний, если в начальный момент φ=0,0600 рад, φ=0,800 рад/с.
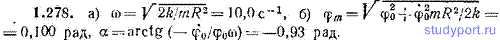
1.279. Два диска могут вращаться без трения вокруг горизонтальной оси. Радиус дисков одинаков и равен R = 0,500 м. Массы дисков равны: m1 = 2,00 кг и m2 = 3,00 кг. Диски соединены пружиной, у которой коэффициент пропорциональности между возникающим вращательным моментом и углом закручивания равен k = 5,91 Н*м/рад. Диски поворачивают в противоположные стороны и отпускают. Чему равен период m крутильных колебаний дисков? Диаметром оси пренебречь.
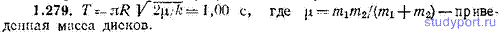
1.280. По диаметру горизонтального диска может перемещаться, скользя без трения по направляющему стержню, небольшая муфта массы m=0,100 кг. Муфта «привязана» к концу стержня с помощью невесомой пружины, жесткость которой k=10,0 Н/м (рис. 1.48). Если пружина не напряжена, муфта находится в центре диска. Найти частоту ω малых колебаний муфты в том случае, когда диск вращается вокруг своей оси с угловой скоростью φ с точкой, равной: а) 6,00 рад/с, б) 10,1 рад/с.
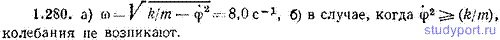
1.281. К куполу зала подвешен на легком нерастяжимом шнуре шар массы m=5,00 кг. Длина подвеса l=9,81 м. Шар отвели в сторону вдоль некоторого направления x на расстояние a=30,0 см и сообщили ему в перпендикулярном к x направлении y импульс p=2,00 кг*м/с. Пренебрегая трением, найти уравнение траектории, по которой будет двигаться центр шара.
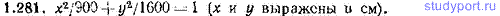
1.282. За 10 с амплитуда свободных колебаний уменьшается в 10 раз. За какое время τ амплитуда уменьшится в 100 раз?

1.283. За 1,00 с амплитуда свободных колебаний уменьшается в 2 раза. В течение какого промежутка времени τ амплитуда уменьшится в 10 раз?

1.284. За время t=16,1 с амплитуда колебаний уменьшается в η=5,00 раз. а) Найти коэффициент затухания колебаний β. б) За какое время τ амплитуда уменьшится в e раз?
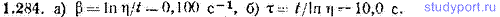
1.285. За 100 с система успевает совершить 100 колебаний. За то же время амплитуда колебаний уменьшается в 2,718 раз. Чему равны: а) коэффициент затухания колебаний β, б) логарифмический декремент затухания λ ,в) добротность системы Q, г) относительная убыль энергии системы -ΔE/E за период колебаний?
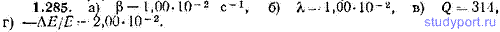
1.286. За время, в течение которого система совершает N = 100 колебаний, амплитуда уменьшается в η = 5,00 раз. Найти добротность системы Q.

1.287. Добротность некоторой колебательной системы Q=2,00, частота свободных колебаний ω=100 с-1. Определить собственную частоту колебаний системы ω0.
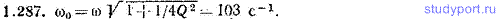
1.288. Затухающие колебания частицы были возбуждены путем смещения ее из положения равновесия на расстояние a0=1,00 см. Логарифмический декремент затухания λ=0,0100. При столь слабом затухании можно с большой степенью точности считать, что максимальные отклонения от положения равновесия достигаются в моменты времени tn=( T/2)n (n=0, 1, 2, . . .). В этом приближении найти путь s, который пройдет частица до полной остановки.
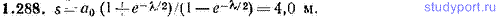
1.289. Частота свободных колебаний некоторой системы ω=100,0 с-1, резонансная частота ωрез=99,0 с-1. Определить добротность Q этой системы.
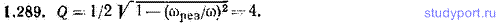
1.290. Железный стержень, подвешенный к пружине, будучи выведен из положения равновесия, совершает свободные колебания частоты ω’=20,0 с-1, причем амплитуда колебаний уменьшается в η=2 раз в течение времени τ=1,11 с. Вблизи нижнего конца стержня помещена катушка, питаемая переменным током (рис. 1.49). При частоте тока ω=11,0 с-1 стержень колеблется с амплитудой а=1,50 мм. а) При какой частоте тока ωрез колебания стержня достигнут наибольшей интенсивности? б) Какова будет амплитуда aрез колебаний при этой частоте? Предполагается, что амплитуда вынуждающей силы неизменна. Учесть, что частота вынуждающей силы равна удвоенной частоте изменений тока в катушке.