59. Докажите, что групповая скорость волн де Бройля равна скорости свободно движущейся частицы. Рассмотрите нерелятивистский и релятивистский случаи.

60. Докажите, что для свободно движущейся с постоянной скоростью v частицы выполняется соотношение vфаз u = c2 (u —групповая скорость).

61. Выведите закон дисперсии волн де Бройля, т.е. зависимость фазовой скорости волн де Бройля от их длины волны. Рассмотрите нерелятивистский и релятивистский случаи.
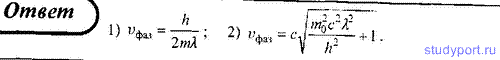
62. Ширина следа электрона (обладающего кинетической энергией T = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет Δx = 1 мкм. Определите, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики.

63. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1% от ее числового значения. Определите неопределенность координаты электрона. Являются ли электроны в данных условиях квантовой или классической частицей?

64. Определите отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью.

65. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определите, можно ли одновременно измерить траекторию электрона с точностью до 100 пм (с точностью порядка диаметра атома) и его скорость с точностью до 10%.

66. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от ее числового значения, определите неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории?

68. Используя соотношение неопределенностей в форме Δx Δpx >= h , оцените минимально возможную полную энергию электрона в атоме водорода. Примите неопределенность координаты равной радиусу атома. Сравните полученный результат с теорией Бора.

70. Воспользовавшись соотношением неопределенностей, оцените размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния (время его жизни равно 10-8 с).

71. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10 с, определите отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом.

72. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электрон-вольтах) неопределенность энергии данного электрона.
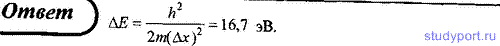
76. Волновая функция, описывающая некоторую частицу, может быть представлена в виде ψ(x, t) = ψ(x)*e –(i/h)*Et . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.
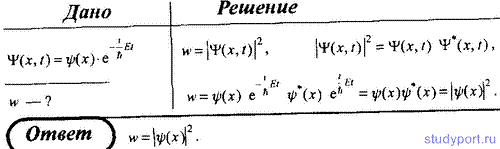
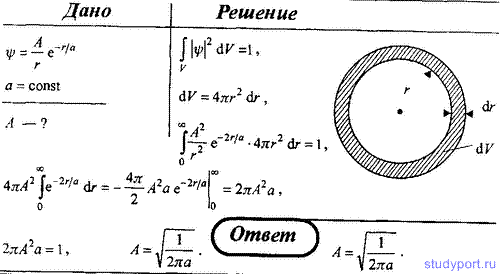
77. ψ-функция некоторой частицы имеет вид ψ = A/r*e-r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Используя условие нормировки вероятностей, определите нормировочный коэффициент A.
78. Используя условие нормировки вероятностей, определите нормировочный коэффициент А волновой функции ψ = A*е-r/a, описывающей основное состояние электрона в атоме водорода, где r — расстояние электрона от ядра, a — первый боровский радиус.

79. Используя условие нормировки вероятностей, определите нормировочный коэффициент волновой функции ψ(r) = A*e-r^2/(2а^2), описывающей поведение некоторой частицы, где r — расстояние частицы от силового центра; a — некоторая постоянная.

80. Волновая функция ψ = A sin(2πx/l) определена только в области 0 <= x <= l . Используя условие нормировки, определите нормировочный множитель A.

81. ψ-функция некоторой частицы имеет вид ψ = A/r*е-r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.
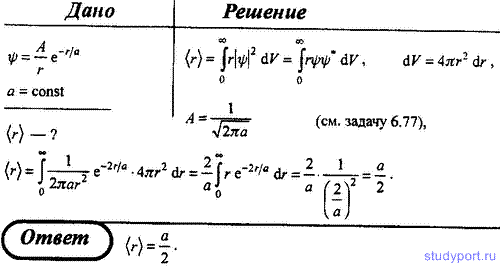
82. Волновая функция, описывающая некоторую частицу, имеет вид ψ = A*e-r^2/(2a^2), где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.


